拓扑学笔记

发表于 2023-09-21 更新于 2024-01-04 分类于数学

Markdown 源代码：https://pastebin.ubuntu.com/p/Jvm2f6jWhW/

分节次的笔记（清华云盘）：https://cloud.tsinghua.edu.cn/d/2c4efaca588a4326958d/

00. Lecture Info

1. 考核

作业 20%、期中 30%、期末 50%

2. 作业

每周四上午 9：50 之前提交

3. 答疑

周二下午 2:00-3:00 荷二 103

4. 内容

基础内容：点集拓扑、代数拓扑
拓展内容；

一点牢骚

很好，又是用 md 追赶手写板书的一门课程，竟然也是英文板书。希望不要像复分析一样上到一半就没兴趣追了（

01. 引入：范畴与连续映射入门

拓扑学研究的范畴

范畴的观点（Categories）
- 研究对象（Objects）
- 态射（Morphism）
这些观点通常对应了数学中的不同分支（Subjects）

eg.

线性代数对应线性范畴（研究对象：线性空间；态射：线性映射）

抽象代数对应群范畴（研究对象：群；态射：群同态）

类似：环范畴、环、环同态

拓扑学对应拓扑空间范畴（研究对象：拓扑空间；态射：连续映射）
拓扑学研究的例子

凸多面体的欧拉公式（Euler's Formula）：设 $\chi=v-e+f$ ，其中 $v$ 是顶点个数，$e$ 是棱的个数，$f$ 是面的个数（vertice, edge, face），则 $\chi=2$。称 $\chi$ 为欧拉示性数（Euler Characteristic）

另一个例子：仍然取一个凸多面体，但在上面挖掉小立方体，如下图所示：

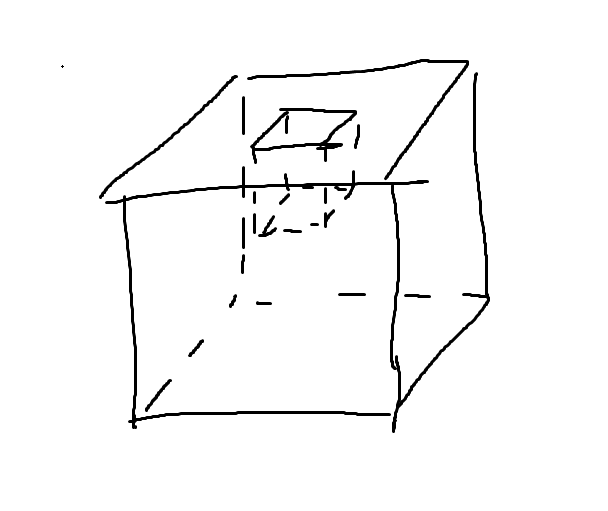
在这种情况下，上半面不能再称之为面（不再单连通），需要多加一条棱如下图所示：

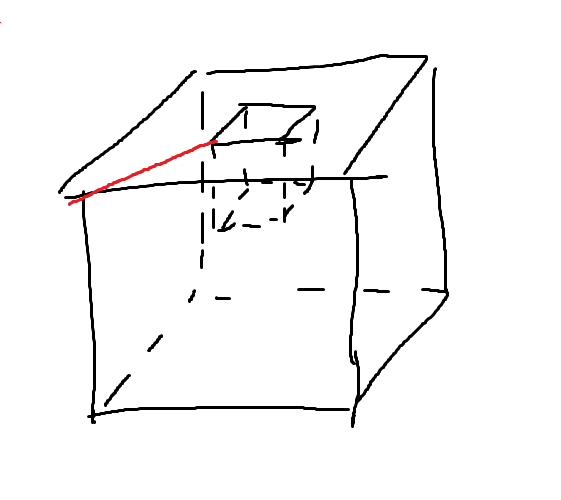
在增加一条棱后，计算此时的欧拉示性数有 $\chi=2$.

进一步地：

仍然对大的立方体做操作，如图所示：

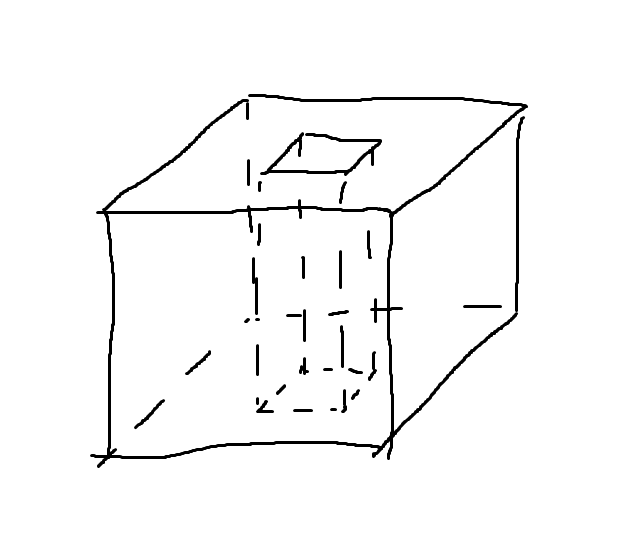
我们做类似的操作切面：

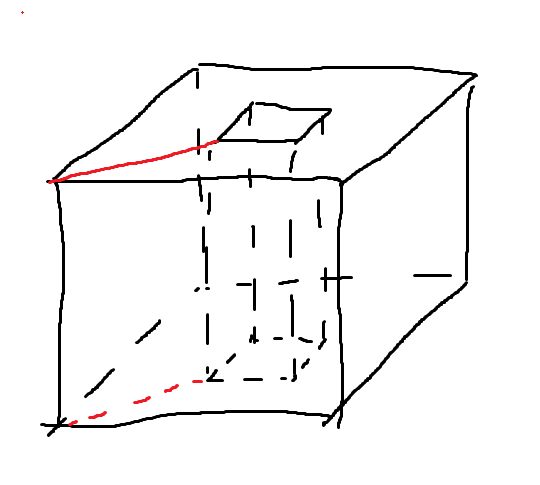
然而此时的 $\chi=0$，不再为 $2$ 了。（为什么？最后一个图形无法通过连续形变变成球面，只能变成环面（Torus=:$T$））

将来我们会证明关于欧拉示性数的事实：$\chi(S^2)=2$；$\chi(T)=0$

更一般地，令 $\sum_g$ 为形如下图的曲面：

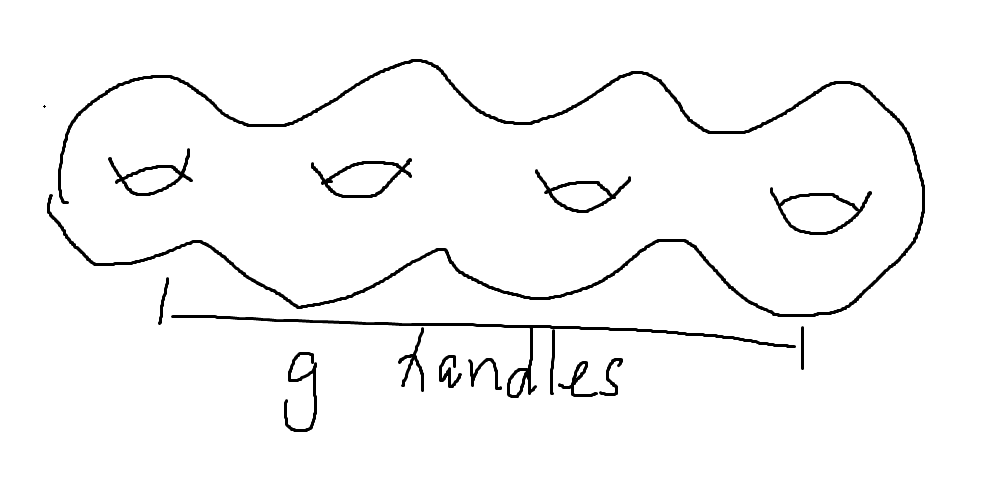
那么有 $\chi(\Sigma_g)=2-2g$.

于是有下述结论：欧拉示性数 $\chi$ 是一个拓扑不变量（Topological Invariant），拓扑不变量也将是这门课程研究的重点。

所谓拓扑不变量指的是：
- 其被连续的形状变化所保持。
- 拓扑不变量可以是数字，也可以是更复杂的代数结构，例如群或环。
- 拓扑不变量是拓扑学这门课程主要研究的对象。
连续映射
- 数学分析对连续映射的定义
  
  $f:\mathbb R^m\to \mathbb R^n$
  
  定义：映射 $f$ 被称为是在 $x\in \mathbb{R}^m$ 连续的，如果有 $\forall \varepsilon>0,\exists \delta>0$，使得若 $|x'-x|<\delta$，则 $|f(x')-f(x)|<\varepsilon$。
  
  如果 $f$ 在 $\mathbb R^m$ 处处连续，则称 $f$ 是连续函数。
- 度量 (Metric)
  
  回顾欧氏空间中在 $R^n $ 上的 $|\cdot |$，它诱导了连续性。
- 度量空间 (Metric Space)
  
  定义：集合 $X$ 被称为是一个度量空间，如果存在映射 $d:X\times X\to \mathbb R$，满足下面几个公理
  - $d(x_1,x_2)=0$ 当且仅当 $x_1=x_2$；
  - $d(x_1,x_2)=d(x_2,x_1)$（对称性）；
  - $d(x_1,x_3)\leq d(x_1,x_2)+d(x_2,x_3)$（三角不等式）；
  $\forall x_1,x_2,x_3\in X$，则称 $d$ 是一个度量，$(X,d)$ 是一个度量空间。
  
  注：由三条公理可以推出距离的非负性：令 $x_1=x_3$，有 $d(x_1,x_3)\leq 2 d(x_1,x_2)$，从而 $d(x_1,x_2)\geq 0$.
- 基础的度量空间例子
  - $\forall x_1=(x_1^1,\cdots,x_1^n),x_2=(x_2^1,\cdots,x_2^n)\in \mathbb R^n$，令 $d(x_1,x_2)=\sqrt{\sum_{i=1}^n(x_1^i-x_2^i)^2}$，则 $(\mathbb R^n,d)$ 是一个度量空间（最熟悉的欧式空间）
  - 更一般地，考虑令 $p\geq 1$，令 $d_p(x_1,x_2)=(\sum_{i=1}^n|x_1^i-x_2^i|^p)^{1/p}$，则 $(\mathbb R^n,d_p)$ 也是一个度量空间
  - 有度量空间 $(X,d)$，考虑子集 $Y\subset X$，则 $(Y,d|_{Y})$ 是一个度量空间
- 度量空间连续性的定义
  
  令 $f:X\to Y$ 度量空间间的映射，定义：
  
  称 $f$ 在点 $x\in X$ 处是连续的，如果 $\forall \varepsilon>0,\exists\delta>0$，使得 $d(f(x),f(x'))<\varepsilon$ 若 $d(x,x')<\delta$.
  
  称 $f$ 是连续的如果 $f$ 对于每一个 $x\in X$ 都是连续的。
- 引入：球的概念
  
  对于 $\varepsilon>0$ 以及任意的 $x\in X$，记 $B(x,\varepsilon):=\{y\in X\mid d(x,y)<\varepsilon\}$，称该集合为一个球，球心为 $x$，半径为 $\varepsilon$。
  
  用以改进连续性：$f$ 是 $x$ 是连续的等价于 $\forall\varepsilon>0,\exists \delta>0$，使得 $f(B(x,\delta))\subset B(f(x),\varepsilon)$.
- 定义：开集 (Open Set)
  
  定义 $X$ 是一个度量空间（今后度量空间略去 $d$），一个集合 $U\subset X$ 称为是开集，若 $\forall x\in U$，$\exists\varepsilon>0$，使得 $B(x,\varepsilon)\subset U$.
  
  与此同时，$\forall x\in U$，我们将 $U$ 称作 $x$ 的一个邻域 (Neighborhood)。
  
  事实：$\forall x\in X,\varepsilon>0$，则 $B(x,\varepsilon)$ 一定是开集。
- 定理 (开集)
  - 1. 任取一个指标集 $I$（可以为无限集），并集 $\bigcup_{i\in I}U_i$ 是 $X$ 中开集若 $U_i$ $\forall i\in I$ 都是开集.（开集的无限并是开）
  - 1. 取交集 $\bigcap_{i=1}^n U_i$ 仍然是开集若 $U_i\ \forall i=1,2,\cdots,n$ 都是开集.（开集的有限交是开）
  - 1. 全空间 $X$ 与空集 $\varnothing$ 都是开集.
  证明：
  - 1. 任取 $x\in \bigcup_{i\in I}U_i$，则 $x\in U_i$ 对于某个特定的 $i$，于是 $\exists B(x,\varepsilon)\subset U_i$，因而 $B(x,\varepsilon)\subset \bigcup_{i\in I}U_i$.
  - 1. $\forall x\in \bigcap_{i=1}^n U_i$，则 $x\in U_i, \forall i$，则 $\exists B(x,\varepsilon_i)\subset U_i$，因而 $B(x,\min_i{\varepsilon_i})\subset \bigcap_{i\in I}U_i$.
  - 1. 显然。
  注：如果取任意交集 $\bigcap_{i\in I} U_i$，一般情况下，该交集可以不是开集（其中 $U_i$ 皆为开集）。
  
  例如令 $U_i=\mathbb R \setminus \{\cfrac{1}{i}\}$，取交集 $\bigcap_{i=1}^\infty U_i=\mathbb R\setminus \{1,\cfrac{1}{2},\cdots\}$，该集合不再是 $\mathbb R$ 里的开集。（对于 $0$，不存在一个球使其包含在该集合中）
- 定义：闭集 (Close Set)
  
  一个集合 $F\subset X$ 被称为是闭 (Close)的，若 $X\setminus F$ 是开集。
- 关键定理 (连续性)
  
  令 $f:X\to Y$ 其中 $X,Y$ 是度量空间，则 $f$ 是连续映射当且仅当 $f^{-1}(U)$ 在 $X$ 中是开的，$\forall U\subset Y$ 开集。
  
  证明：
  
  $(\Rightarrow)$：考虑 $\forall x\in f^{-1}(U)$，我们选取 $B(f(x),\varepsilon)\subset U$，由于 $f$ 是连续的，有 $\exists \delta$ 使得 $f(B(x,\delta))\subset B(f(x),\varepsilon)\subset U$.
  
  换言之，$B(x,\delta)\subset f^{-1}(U)$，于是 $f^{-1}(U)$ 是开集。
  
  $(\Leftarrow)$：考虑 $\forall x\in X$，考虑小球 $B(f(x),\varepsilon)\subset Y$，于是 $f^{-1}(B(f(x),\varepsilon))\subset X$ 是开集。
  
  于是 $\exists \delta>0$，使得 $B(x,\delta)\subset f^{-1}(B(f(x),\varepsilon))$，于是 $f(B(x,\delta))\subset B(f(x),\varepsilon)$，于是 $f$ 是连续函数。
- 定义：拓扑空间 (Topological Space)
  
  一个集合 $X$ 被称为是拓扑空间，若存在 $X$ 的子集族 $\tau$，将该子集族中的集合称之为开集，使得：
  - $X,\varnothing\in \tau$
  - $\forall$ 指标集 $I$，若 $\forall i\in I,U_i\in \tau$，则 $\bigcup_{i\in I}U_i\in \tau$
  - $U_i\in\tau,\forall i=1,\cdots,n$，则 $\bigcap_{i=1}^n U_i\in \tau$
  则称 $X$ 是一个拓扑空间，称 $\tau$ 为 $X$ 上的一个拓扑。
- 例子
  - 度量空间是特殊的拓扑空间：若 $(X,d)$ 是一个度量空间，则 $d$ 一定诱导了一个 $X$ 上的拓扑。
  - （子空间拓扑）若 $Y$ 是 $X$ 的子集，$\tau$ 是 $X$ 上的一个拓扑，则 $\tau$ 可以诱导一个 $Y$ 上的拓扑 $\tau|_Y$：
    
    $\forall V\subset Y$，我们称 $V$ 是 $Y$ 里的开集，若 $V$ 可以被写成如下的形式：$U\cap Y$，其中 $U\in \tau$.
    
    可以验证 $(Y,\tau|_Y)$ 是一个拓扑空间。将这个拓扑空间称为 $(X,\tau)$ 的子空间。
- 定义：连续映射
  
  令 $f:X\to Y$ 是一个拓扑空间间的映射，$f$ 被称为连续映射，如果 $\forall U\subset Y$ 开集，$f^{-1}(U)$ 是 $X$ 中开集。
  
  由此推出拓扑范畴：拓扑空间与拓扑空间的连续映射。

*一个可能不那么典型的例子（拓扑可以非常丰富）

通常地，$\mathbb R$ 上的欧式度量会诱导 $\mathbb R$ 上的拓扑；继续取子空间，则其可以诱导一个 $\mathbb Q$ 上的拓扑。

我们换一种度量的观点：令 $p$ 是一个素数，对于非零有理数 $a=p^m\cfrac{b}{c}$，其中 $b,c$ 与 $p$ 互素。定义 $p\text{-adic}$ 测量 (p-adic evaluation)：$v_p:\mathbb Q\to\mathbb Z\cup\{\infty\}$，$v_p(a)=m$，$v_p(0)=\infty$.

于是：

$v_p(a)=\infty$ 当且仅当 $v_p(a)=0$
$v_p(ab)=v_p(a)+v_p(b)$

于是定义 $p\text{-adic}$ 绝对值：$||\cdot||_p$ 为 $||a||_p=p-v_p(a)$

定义 $d(a,b):=||a-b||_p$ 称为一个 $p\text{-adic}$ 度量（p-adic metric），这会诱导 $p\text{-adic}$ 拓扑。

02. 闭集与连续映射

对闭集的研究

回忆：闭集的定义

一个集合 $A\subset X$ 是闭集当 $X\setminus A$ 是开集。
一些例子

$A=\{(x,y)\mid x^2+y^2=1\}\subseteq \mathbb R^2$ （此后，若不加特殊说明，空间皆使用欧氏拓扑）

它是一个闭集。

$A=\{(x,y)\mid x^2+y^2\leq 1\}\subseteq \mathbb R^2$

它也是一个闭集。

$A=\{(x,y)\mid x^2+y^2=1,y>0\}\subseteq \mathbb R^2$

它不是开集，也不是闭集。
极限点 (limit point) 的定义

定义：令 $A\subset X$，$p\in X$，$p$ 是集合 $A$ 的极限点 (limit point) 如果其任意一个邻域都包含了 $A-\{p\}$ 中至少一个点。

例子：
- 令 $X=\mathbb R$，欧氏拓扑，令 $A=\{\cfrac{1}{n}\mid n=1,2,3,\cdots\}$，则 $A$ 有唯一一个极限点 $0$.
- 令 $X=\mathbb R$，$A=[0,1)$，则 $\forall p\in A$，$p$ 是 $A$ 的一个极限点，与此同时 $1$ 也是 $A$ 的极限点。
- 令 $X=\mathbb R$，$A=\mathbb Q$，则 $\forall p\in X$ 都是 $A$ 的极限点。
- 令 $X=\mathbb C$，在 $\mathbb C$ 上定义 Zariski Topology，定义 $X$ 的一个子集是开集，如果它的补集是有限集或全空间 $X$.
  
  考虑 $f(t)\in \mathbb C[t]$ 是一个复系数单变量多项式，即 $f(t)$ 可以写成如下形式：$a(t-a_1)\cdots(t-a_n)$. 其中 $a_1,\cdots,a_n\in \mathbb C$。
  
  一个集合 $A\subset X$ 是闭集，当且仅当 $A$ 是有限集或 $A$ 是全空间 $X$，这等价于 $A$ 是某一个多项式的零点集。这即为 Zariski Topology 的定义动机。
  
  我们来考察极限点。若集合 $A$ 是有限集，那么 $A$ 没有极限点；若集合 $A$ 是无限集，则任意 $p\in X$ 都是 $A$ 的极限点。
  
  (*)更多地，我们还可以考虑 Zariski Topology 在 $\mathbb C^n$ 时的情形。
  
  一个集合 $A\subseteq \mathbb C^n$ 是闭集，如果 $A$ 是某一些多项式的零点 $f_1,f_2,\cdots,f_m\in \mathbb C[t_1,\cdots,t_n]$.
闭集一般性的定义

定理：一个集合是闭集，当且仅当它包含了自己的所有极限点。

证明：

$(\Rightarrow)$：令 $A\subset X$ 是一个闭集，根据定义，$X\setminus A$ 是一个开集。于是 $\forall p\in X\setminus A$，有 $X\setminus A$ 是 $p$ 的邻域，且该邻域与 $A$ 不交。于是 $p$ 不是 $A$ 的极限点。

$(\Leftarrow)$：令 $p\in X\setminus A$，因为 $p$ 不是 $A$ 的极限点，$\exists$ 邻域 $U_p$，使得 $U_p\subset X\setminus A$，因而 $X\setminus A=\bigcup_{p\in X\setminus A} U_p$ 是开集，因此 $A$ 是一个闭集。
闭包 (closure) 的定义

定义：从集合 $A$ 出发，将 $A$ 本身与它所有的极限点并起来，将这称作集合 $A$ 的闭包，记作 $\bar A$.

定理：$A$ 的闭包是包含 $A$ 的最小闭集。
- 对定理中“最小”的解释
  
  有两种不同的（等价的）表达方式。
  - $\bar A=\bigcap_{B\supset A, B\text{ is closed}} B$
  - $\bar A$ 是闭集，且对于 $\forall B\supset A$ 且 $B$ 为闭集，都有 $A\subset\bar A\subset B$.
证明：

首先证明 $\bar A$ 是一个闭集。

$\forall p\in X\setminus \bar A$，$p$ 一定不是 $A$ 的极限点，于是 $\exists$ 邻域 $U_p$ 使得 $U_p\cap A=\varnothing$.

另一方面，$\forall q\in U_p$，有 $U_p$ 也是 $q$ 的邻域，因此 $q$ 不是 $A$ 的极限点。因此 $U_p\cap \bar A=\varnothing$.

因此 $U_p\subset X\setminus \bar A$，因此 $X\setminus \bar A=\bigcup_{p\in X\setminus \bar A}U_p$，因此 $X\setminus \bar A$ 是开集，因此 $\bar A$ 是闭集。

接着我们来证明最小性。

若 $B$ 是一个闭集且 $A\subset B$，则有 $\forall$ $A$ 的极限点也是 $B$ 的极限点。因为 $B$ 是闭集，这些极限点都落在其中，于是 $B$ 包含了所有 $A$ 的极限点。因此 $\bar A\subset B$.

推论：若 $A\subset X$，则 $A$ 是闭集当且仅当 $A=\bar A$.
稠密 (dense) 的定义

定义：$A\subset X$ 被称为是稠密的，如果 $\bar A=X$.

例子：$\mathbb{Q}\subseteq\mathbb{R}$ 是稠密的。
内部点 (interior point) 的定义

定义：$x\subset A$ 被称作一个内部点当 $\exists$ $x$ 的邻域 $U$ 使得 $U\subseteq A$.

记 $\mathring A=\{x\in A\mid x \text{ 是内部点}\}$.

例子：

令 $A=\{(x,y)\mid x^2+y^2\leq 1\}\subseteq \mathbb R^2$，则 $\mathring A=\{(x,y)\mid x^2+y^2<1\}\subseteq \mathbb R^2$
边界点 (frontier point / boundary point) 的定义

定义：$x\in X$ 被称为 $A$ 的边界点（请注意定义域），如果 $x$ 既不是 $A$ 的内部点也不是 $X\setminus A$ 的内部点。

例子：

$A_1=\{(x,y)\mid x^2+y^2\leq1\}\subseteq \mathbb R^2$，若定义 $C=\{(x,y)\mid x^2+y^2=1\}$，则 $C$ 就是 $A_1$ 边界点的集合。

$A_2=\{(x,y)\mid x^2+y^2<1\}\subseteq \mathbb R^2$，仍如上定义 $C$，则 $C$ 也是 $A_2$ 边界点的集合。

（$A$ 的边界点未必包含于 $A$ 中）

$0,1$ 都是下面集合的边界点：$[0,1)\subseteq \mathbb{R}$.
拓扑基 (basis / base) 的定义

定义：令 $\beta$ 是一个由某一些 $X$ 中开集构成的集族，假设 $X$ 中的每一个开集都可以表示为 $\beta$ 中成员的并，则称 $\beta$ 是 $X$ 的一组基。把 $\beta$ 中的元素称作基础开集。

例子：

$X$ 是度量空间，则 $\beta:=\{B(x,\varepsilon)\mid x\in X,\varepsilon>0\}$ 是 $X$ 的一组拓扑基。

定理：令 $X$ 是一个集合，令 $\beta$ 是 $X$ 中集族且 $\beta$ 不为空，假设 $\bigcup_{B\in\beta}B=X$ 且 $\forall B_1,B_2\in \beta$，$\forall x\in B_1\cap B_2$，$\exists B_{3}^x\in \beta$，使得 $x\in B_{3}^x$ 且 $B_{3}^x\subset B_1\cap B_2$，则我们可以定义 $X$ 中开集为 $\beta$ 中成员的任意并，则这个定义给出了 $X$ 上的一个拓扑。

证明：$U_i=\bigcup_j B_{ij}$，$B_{ij}\in \beta$，$\bigcup_i U_i=\bigcup_{ij}B_{ij}$，因此为开；

$U_1=\bigcup_{i}B_{1i}$，$U_2=\bigcup_{j}B_{2j}$，$B_{1i}B_{2j}\in \beta$，则 $U_1\cap U_2=\bigcup_{ij}(B_{1i}\cap B_{2j})$ ，因此只需要证明 $\forall B_1,B_2\in\beta$，有 $B_1\cap B_2$ 为开集。证明：$\forall x\in B_1\cap B_2$，$\exists B_{3}^x$ 使得 $x\in B_{3}^x$，有 $B_{3}^x\subset B_1\cap B_2$，因此 $\bigcup_{x\in B_1\cap B_2} B_{3}^x=B_1\cap B$ 是开集.

显然 $X,\varnothing$ 都是开集。综上这构成拓扑。

对连续映射的研究

回忆：连续映射

$f:X\to Y$ 是连续映射，当且仅当开集的原像也是开集。
连续映射的复合

定理：若有映射 $f:X\to Y$ 与映射 $g:Y\to Z$，若两个映射都是连续映射，则 $g\circ f$ 仍然是连续映射。

证明：根据定义，任取 $U\subset Z$ 为开集，根据连续性，有 $g^{-1}(U)$ 在 $Y$ 中是开集，进一步其在 $f^{-1}(g^{-1}(U))$ 在 $X$ 中是开集。因此得出结论。
限制到子空间的连续性

定理：令 $f:X\to Y$ 是连续映射，取子空间 $A\subseteq X$ 采用子空间拓扑，则 $f|_A:A\to Y$ 仍然是连续映射。

证明：令 $U\subset Y$ 是一个开集，因此 $f^{-1}(U)$ 是 $X$ 中开集，则 $(f|_A)^{-1}(U)=A\cap f^{-1}(U)$，其为 $A$ 中开集。因此得出结论
连续性的等价叙述

定理：下面的叙述是等价的：
1. $f:X\to Y$ 是连续映射；
2. 若 $\beta$ 是 $Y$ 的拓扑基，基础开集的原像还是开集；
3. $f(\bar A)\subset \overline{f(A)}, \forall A\subset X$
4. $\overline{f^{-1}(B)}\subset f^{-1}(\bar B),\forall B\subset Y$.
5. $f^{-1}(A)$ 总是一个闭集，$\forall$ 闭集 $A\subset Y$.
证明：

$(1)\Rightarrow (2)$ 显然成立；

$(2)\Rightarrow(3)$：$f(A)\subset \overline{f(A)}$ 是显然的。令 $x\in \bar A\setminus A$。假设 $f(x)\not\in f(A)$，令 $U$ 是一个 $f(x)$ 在 $Y$ 中邻域，可以找到一个基础开集 $B$ 使得 $f(x)\in B\subset U$.

由于 $f^{-1}(B)$ 是开集且 $x\in f^{-1}(B),x\in \bar A\setminus A$，有 $f^{-1}(B)\cap A\neq \varnothing$，于是 $f(A)\cap B\neq \varnothing$，于是 $f(A)\cap U\neq\varnothing$。

介于 $U$ 的任意性，于是 $f(x)$ 是 $f(A)$ 的极限点，于是得出结论。

$(3)\Rightarrow (4)$：$f(\overline{f^{-1}(B)})\subset \overline{f(f^{-1}(B))}\subset \overline B$，因此 $\overline{f^{-1}(B)}\subset f^{-1}(\bar B)$。

$(4)\Rightarrow (5)$：令 $B\subset Y$ 是闭集，则 $B=\bar B$，于是 $\overline{f^{-1}(B)}\subset f^{-1}(\bar B)=f^{-1}(B)$，因此 $f^{-1}(B)=\overline{f^{-1}(B)}$，因此 $f^{-1}(B)$ 是闭集。

$(5)\Rightarrow(1)$：显然。

03. 同胚、距离与度量空间

对连续映射的进一步研究

同胚 (Homeomorphism) 的定义

称 $f:X\to Y$ 是同胚，如果 $f$ 是连续，且存在逆映射：$g:Y\to X$ 使得 $g$ 也是连续映射，且 $f\circ g=id_Y,g\circ f=id_X$.

同胚就是拓扑范畴中的同构。

注：如果 $f:X\to Y$ 是一个连续映射，并且这个映射是一个双射，一般情况下 $f$ 不是一个同胚。（拓扑范畴不能以以前的逻辑进行考虑）

例如：从半开半闭的线段映射到圆周，逆映射并不是一个连续映射。

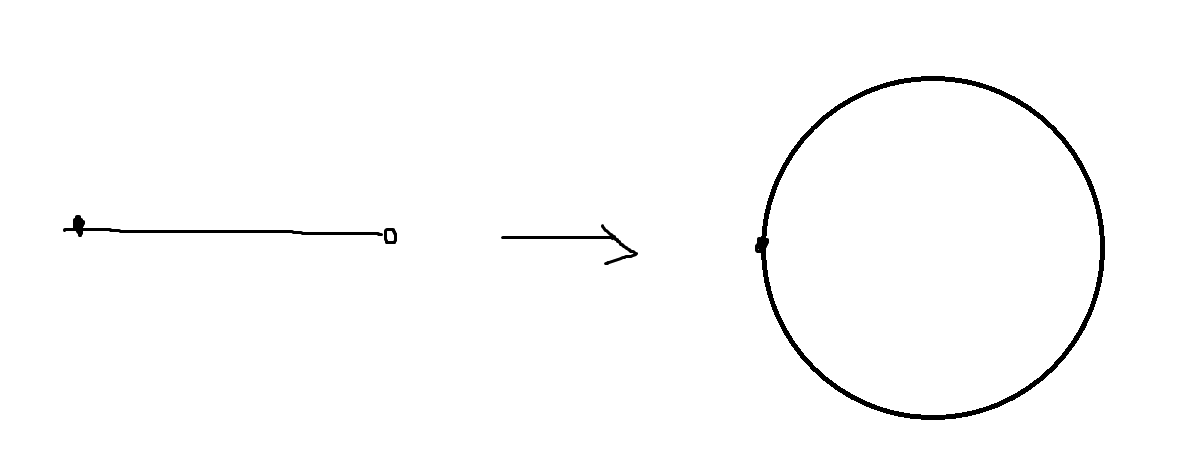
$[0,1)\to S'=\{(x,y)\mid x^2+y^2=1\}, x\to (\cos 2\pi x,\sin 2\pi x)$
连续映射的局部性质 (Local formulation of continuity)
1. $f:X\to Y$ 是一个连续映射，如果 $X$ 可以被一些开集 $U_\alpha$ 覆盖，即 $X=\bigcup_\alpha U_\alpha$，使得 $f|_{U_\alpha}$ 是连续的。
2. $f:X\to Y$ 是一个连续映射，如果 $X$ 可以表示成一些闭集 $F_i$ 的并，即 $X=\bigcup_{i=1}^n F_i$，且 $f|_{F_i}$ 是连续的。
证明：
1. 任取 $V\subset Y$ 是开集，由定义，$f^{-1}(V)=\bigcup_{\alpha} f|_{U_\alpha}^{-1}(V)$，其中 $f|_{U_\alpha}^{-1}(V)$ 是 $U_\alpha$ 中开集. 由于 $U_\alpha$ 是 $X$ 中开集，有 $f|_{U_\alpha}^{-1}(V)$ 也是 $X$ 中开集，于是 $f^{-1}(V)$ 是开集，因此 $f$ 是连续函数。
2. 任取 $V\subset Y$ 是闭集，有定义，$f^{-1}(V)=\bigcup_{i=1}^n f|_{F_i}^{-1}(V)$，其中 $f|_{F_i}^{-1}(V)$ 是 $F_i$ 中闭集. 由于 $F_i$ 是 $X$ 中闭集，有 $f|_{F_i}^{-1}(V)$ 也是 $X$ 中闭集，于是 $f^{-1}(V)$ 是闭集，因此 $f$ 是连续函数。
例子：

考虑分段函数：$f(x)=\begin{cases}x-1&x<0\\x+1&x\geq0\end{cases}$，这自然不是一个连续函数。

然而 $f|_{[0,+\infty)}, f|_{(-\infty,0)}$ 都是连续的，并且 $\mathbb R=[0,+\infty)\cup(-\infty,0)$，因为该覆盖既并非全是开集，又并非全是闭集，故无法套用上述定理。（上述定理的“开”、“闭”是必要的）
拓扑学中的极限 (Limit)

令 $X$ 是一个集合，令 $\beta$ 是一个子集族，使得其满足：
- $\forall B\in\beta,B\neq\varnothing$
- $\forall B_1,B_2\in\beta,\exists B_3\in \beta,s.t. B_3\subset B_1\cap B_2$
则称 $\beta$ 是集合 $X$ 的一组基 (basis)。

定义：设映射 $f:X\to Y$，其中 $X$ 装备了一组基 $\beta$，$Y$ 是一个拓扑空间。考虑点 $p\in Y$，我们将 $p$ 称作是 $f$ 在基 $\beta$ 下的极限，如果 $\forall$ $p$ 的邻域 $V$，$\exists A\in \beta$，使得 $f(A)\subset V$. 记作 $\lim_{\beta} f(x)=p$.

例子：

回忆：在数学分析中我们学过，$\lim_{x\to a} f(x)=p\in \mathbb R$，$f:\mathbb R\setminus\{a\}\to \mathbb R$.

我们令 $X=\mathbb R\setminus \{a\},Y=\mathbb R$. 令 $\beta=\{\mathring U(a)\setminus\set a\mid U(a) \text{ 是 a 的邻域}\}$。

将 $X$ 看成集合，$Y$ 是拓扑空间，$\beta$ 是 $X$ 上的一组基。

有 $\lim_{x\to a}f(x)=p\Leftrightarrow \lim_{\beta} f(x)=p$

另一个例子（较为复杂的情形）：黎曼积分 (Riemann Integral)

令 $I\subset \mathbb R$ 是一段区间，令 $I=\bigcup_{i=1}^n I_i$ 使得 $I_i$ 是区间且任意两个子区间 $I_i,I_j$ 内部没有公共内点，则我们称这组小区间 $\set{I_i}$ 是大区间的分划 (Partition)。

有时我们把一个分划记作 $P$.

给出一个分划，我们将分划中小区间的最大长度记作 $\lambda(P)$.

如果我们在每一个小区间里都固定一个点 $\xi_i\in I_i$，则称我们有了一个带标志点的分划，记作 $(P,\xi)$。

令 $\mathscr{P}$ 为所有带标志点的分划组成的集合，考虑一组基 $\beta$：$\beta:=\set{B_d}_{d>0}$，其中 $B_d:=\set{(P,\xi)\in\mathscr P\mid \lambda(P)\leq d}$.

我们把 $\beta$ 记作 $\lambda(P)\to 0$.

进一步给出下面的定义：令 $f$ 是 $I\to\mathbb R$ 上的函数，$(P,\xi)$ 是一个带标志点的分划，则把下面的求和：$\sigma(f,P,\xi)=\sum_{i=1}^n f(\xi_i)|I_i|$ 称作 $f$ 在 $(P,\xi)$ 上的黎曼和 (Riemann Sum)。

可以将 $\sigma$ 看成是一个 $\mathscr P\to \mathbb R$ 的映射。

定义 $f$ 在 $I$ 上的黎曼积分：$\lim_{\beta} \sigma(f,P,\xi)$ 或者 $\lim_{\lambda(P)\to 0}\sigma(f,P,\xi)$.

如果该极限存在，则我们将其记作 $\int_I f(x)\text{d}x$.

对度量空间的研究

度量空间的扩张/延拓 (Extension Problem)

$X$ 是一个度量空间，$A\subset X$，考虑映射 $f:A\to \mathbb R$，使得 $f$ 是一个连续映射。

扩张问题说的是，是否可以将 $f$ 连续地延拓到全空间 $X$ 上？

事实上，很多时候并不可以。例子：$X=[-\cfrac{\pi}{2},\cfrac{\pi}{2}],A=(-\cfrac{\pi}{2},\cfrac{\pi}{2})$，$f(x):\tan(x)$.

此时无法将 $f$ 连续地延拓至 $X$ 上。
点到集合距离的定义

令 $d$ 是一个 $X$ 上的度量，令 $A\subset X$，$\forall x\in X$ 定义 $d(x,A):=\inf_{a\in A}d(x,a)$.

引理：考虑函数 $x\to d(x,A)$，则该函数是一个连续函数。

证明：$\forall \varepsilon>0$，考虑 $(d(x,A)-\varepsilon,d(x,A)+\varepsilon)$，令 $U=B(x,\cfrac{\varepsilon}{2})$，选取 $a\in A$ 使得 $d(x,a)<d(x,A)+\cfrac{\varepsilon}{2}$.

$\forall y\in U$，有 $d(y,A)\leq d(y,a)\leq d(y,x) + d(x,a)<\cfrac{\varepsilon}{2}+\cfrac{\varepsilon}{2}+d(x,A)=d(x,A)+\varepsilon$.

反过来，还有 $d(x,a)<d(y,a)+\varepsilon$，因而 $d(y,A)\in (d(x,A)-\varepsilon,d(x,A)+\varepsilon)$.

因此 $x\to d(x,A)$ 是连续函数。

引理：$A,B\subset X$ 是闭集且 $A\cap B=\varnothing$，则 $\exists f:X\to \mathbb R$ 是连续函数且 $f|_A=1,f|_B=-1$，$f|_{X\setminus (A\cup B)}\subset(-1,1)$.

证明：对任意的 $x\in X$，假设 $d(x,A)=0$ 且 $x\not \in A$，根据距离的定义，存在序列 $\set{a_n}\subset A$，使得 $\lim_{n\to\infty} d(x,a_n)=0$，因此 $x$ 是一个 $A$ 的极限点. 由于 $A$ 是闭的，一定有 $x\in A$，导出矛盾。

因此，如果 $x\not\in A$，则 $d(x,A)>0$. 类似地，如果 $x\not\in B$，则 $d(x,B)>0$.

如果 $A\neq\varnothing,B\neq\varnothing$，令 $f(x)=\cfrac{d(x,B)-d(x,A)}{d(x,A)+d(x,B)}$，该函数分母一定 $>0$.

显然 $f|_A=1,f|_B=-1$.

如果 $x\in X\setminus (A\cup B)$，则 $d(x,A)>0,d(x,B)>0$，有 $f(x)\in (-1,1)$.

且由前一个引理，$f$ 确实是连续函数。

如果 $B=\varnothing$，则令 $f(x)=\cfrac{1}{d(x,A)+1}$；

如果 $A=\varnothing$，则令 $f(x)=\cfrac{-1}{d(x,B)+1}$；

如果 $A=B=\varnothing$，则令 $f(x)=0$.
扩张定理 (Tietze extension theorem)

令 $X$ 是度量空间，$C\subset X$ 是闭集。若 $f:C\to \mathbb R$ 连续，则 $f$ 可以被连续地延拓到全空间 $X$ 上。

证明：

Step 1. 假设 $f:C\to \mathbb R$ 是一个有界函数，也就是 $\exists M>0$，使得 $|f(x)|\leq M,\forall x\in C$.

令 $A_1:=f^{-1}([\cfrac{M}{3},+\infty)), B_1:=f^{-1}((-\infty,-\cfrac{M}{3}])$，此时 $A_1,B_1$ 是 $C$ 中闭集。

由于 $C$ 是 $X$ 中闭集，有 $A_1,B_1$ 也是 $X$ 中闭集。

由前一个引理，$\exists g_1$ 使得 $g_1:X\to [-\cfrac{M}{3},\cfrac{M}{3}]$，使得 $g_1|_{A_1}=\cfrac{M}{3},g_1|_{B_1}=-\cfrac{M}{3}$

$g_1|_{X\setminus(A_1\cup B_1)}\subset(-\cfrac{M}{3},\cfrac{M}{3})$

于是 $|f(x)-g_1(x)|\leq \cfrac{2}{3}M$ 于 $C$

类似地，考虑 $A_2=(f-g_1)^{-1}([\cfrac{2M}{9},+\infty))$，$B_2$ 类似，

则 $\exists g_2$ 使得 $g_2|_{A_2}=\cfrac{2M}{9},g_2|_{B_2}=\cfrac{-2M}{9}$

并且 $g_2|_{X\setminus(A_2\cup B_2)}\subset (-\cfrac{2M}{9},\cfrac{2M}{9})$，于是 $|f(x)-g_1(x)-g_2(x)|\leq \cfrac{4M}{9}$

继续执行这一过程，即可得到 $g_n:X\to[-\cfrac{2^{n-1}M}{3^{n}},\cfrac{2^{n-1}M}{3^{n}}]$，有 $|f-\sum_{i=1}^n g_i|\leq\cfrac{2^{n}}{3^n}M$ 于 $C$

因此 $\sum_{n=1}^{\infty} g_n(x)$ 在 $X$ 上一致收敛且连续，令 $g(x)=\sum_{n=1}^{\infty} g_n(x)$，这就是一个 $C$ 至 $X$ 的延拓。

Step 2. 由于 $|g(x)|\leq \sum_{i=1}^n |g_i(x)|\leq \sum_{n=1}^{\infty} \cfrac{2^{n-1}}{3^n}M=M$

有 $|g(x)|<M$ 于 $X\setminus C$.

如果 $f$ 是无界的，则选取同胚 $h:\mathbb R\to(-1,1)$. 考察 $h\circ f$，这是一个有界的函数，可以用 Step 1 延拓。

于是 $\exists g$ 使得 $g$ 是 $h\circ f$ 的延拓，且 $|g(x)|<M=1,\forall x\in X$. 于是 $h^{-1}\circ g(x)$ 是 $f$ 的一个延拓。

04. 度量空间的完备化

度量空间的完备化

完备的度量空间 (Complete metric space)
- 柯西序列 (Cauchy Sequence)
  
  令 $(X,d)$ 是一个度量空间，定义序列 $\set{x_n\mid n\geq 1}$ 被称为柯西序列 (Cauchy sequence)，如果 $\forall \varepsilon>0$，$\exists N\in \mathbb N$，使得 $d(x_m,x_n)<\varepsilon,\forall n,m>N$.
- 点列的极限
  
  对点列 $\set{x_n}\in X$，称其收敛于 $a$，如果 $\lim_{n\to\infty}d(x_n,a)=0$，把点 $a$ 称作点列 $\set{x_n}$ 的极限。
- 完备度量空间的概念
  
  一个度量空间 $(X,d)$，称其是完备的如果 $\forall$ 柯西序列 $\set{x_n}$ 都有极限。
- 例子
  
  $\mathbb R$ 赋予欧氏度量后是完备的度量空间。
  
  $\mathbb Q\subseteq \mathbb R$ 不是完备的。
  
  $\mathbb R\setminus\set{0}$ 不是完备的。（考察 $\set{\cfrac{1}{n}}$）
  
  令 $C[a,b]$ 表示所有 $[a,b]$ 区间上连续函数构成的集合，其中 $[a,b]\subset \mathbb R$，我们定义度量 $d(f,g)=\max_{a\leq x\leq b} |f(x)-g(x)|$，则这是一个完备度量空间。
  
  证明：设 $\set{f_n}$ 是一个柯西序列，使得 $\forall \varepsilon>0$，$\exists N\in \mathbb N$，有 $\forall m,n>N$，有 $|f_n(x)-f_m(x)|<\varepsilon$.
  
  固定 $\forall x\in [a,b]$，则 $\set{f_n(x)}$ 是一个 $\mathbb R$ 中的柯西序列，于是 $\exists$ 极限 $f(x)\in\mathbb R$.
  
  $f(x):=\lim_{n\to\infty}f_n(x)$，$x\in [a,b]$.
  
  目标：证明 $f\in C[a,b]$. 我们考察 $f(x+h)-f(x)$，
  
  $f(x+h)-f(x)=f(x+h)-f_n(x+h)+f_n(x+h)-f_n(x+h)-f_n(x)+f_n(x)-f(x)$.
  
  $\forall \varepsilon>0$，$\exists N$，使得 $n>N$，有 $|f(x)-f_n(x)|<\varepsilon$，类似地，我们选取合适的 $h$，可以使得另外两项也 $<\varepsilon$，因而得到 $|f(x+h)-f(x)|<3\varepsilon$，连续。
  
  仍然考虑连续函数空间，定义度量 $d(f,g)=\int_{a}^b |f-g|(x)\text{d}x$，这将不是一个完备的度量空间。
  
  构造 Cauchy 列：$f_n(x)=\begin{cases}-1&a\leq x\leq \cfrac{a+b}{2}-\cfrac{1}{n}\\n(x-\cfrac{a+b}{2})&\cfrac{a+b}{2}-\cfrac{1}{n}\leq x\leq \cfrac{a+b}{2}+\cfrac{1}{n}\\1&\cfrac{a+b}{2}+\cfrac{1}{n}\leq x\leq b\end{cases}$
  
  图：函数图像示例。
  
  可以发现该 Cauchy 列的极限为 $f(x)=\begin{cases}-1&a\leq x<\cfrac{a+b}{2}\\0&x=\cfrac{a+b}{2}\\1&\cfrac{a+b}{2}<x\leq b\end{cases}$
  
  这不可能是一个连续函数（即使由于度量定义导致 $x=\cfrac{a+b}{2}$ 时取值可变）。
度量空间的完备化 (Completion of a metric space)

令 $(X,d)$ 是一个度量空间，我们想要找到一个最小的完备空间，称之为 $(Y,d)$，使得 $X\subset Y$.

例如，$\mathbb Q$ 不是一个完备的度量空间，我们将 $\mathbb R$ 称作其的完备化。

定义：如果 $(X,d)$ 是 $(Y,d)$ 的子空间，$(Y,d)$ 是完备的并且满足 $X$ 在 $Y$ 中是稠密的（$\bar X=Y$），则把 $(Y,d)$ 称作 $(X,d)$ 的完备化。更进一步地，这种完备化在下面的意义下是唯一的。
度量空间间的 Isometry

称两个度量空间 $(X_1,d_1)$, $(X_2,d_2)$ 是 Isometric 的，当 $\exists$ 双射 $f:X_1\to X_2$，使得双射保持度量结构，即 $d_2(f(a),f(b))=d_1(a,b),\forall a,b\in X_1$. 将映射 $f$ 称作一个 isometry.

回忆：Isometry 与此前的同胚有什么不同？ $f$ 是一个 isometry$\Rightarrow$ $\exists g:X_2\to X_1$，使得 $d_1(g(a),g(b))=d_2(a,b),\forall a,b\in X_2$，其中 $f\circ g=id_{X_2},g\circ f=id_{X_1}$.
度量空间完备化的唯一性 (Uniqueness of Completion)

引理：令 $(X,d)$ 是一个度量空间且 $a,b,u,v\in X$，则 $|d(a,b)-d(u,v)|\leq d(a,u)+d(b,v)$。

证明：$d(a,b)\leq d(a,u)+d(u,b)\leq d(a,u)+d(u,v)+d(v,b)$

于是 $d(a,b)-d(u,v)\leq d(a,u)+d(u,v)$

类似地，$d(u,v)\leq d(u,a)+d(a,b)+d(b,v)$

于是 $d(u,v)-d(a,b)\leq d(u,a)+d(b,v)$

得出结论。

定理：如果 $(Y_1,d_1)$ 以及 $(Y_2,d_2)$ 都是 $(X,d)$ 的完备化，则 $(Y_1,d_1)$ 与 $(Y_2,d_2)$ 是 Isometric 的。

证明：$\forall x\in X$，令 $f(x)=x$；$\forall x_1,x_2\in X$，有 $d_2(f(x_1),f(x_2))=d(f(x_1),f(x_2))=d(x_1,x_2)=d_1(x_1,x_2)$.

我们考虑把 $f$ 延拓到 $Y_1$.

令 $y_1\in Y_1\setminus X$，$y_1$ 是 $X$ 的一个极限点，因此存在序列 $\set{x_n}\subset X$，使得 $x_n\to y_1$（$\lim_{n\to\infty} d_1(x_n,y_1)=0$），同时 $\set{x_n}$ 是一个柯西序列。另一方面，由于 $(Y_2,d_2)$ 是一个完备的空间，则 $\set{x_n}$ 在 $Y_2$ 中也有极限 $y_2\in Y_2$.

我们定义 $f(y_1)=y_2$.

$f$ 自然是满射，这是因为 $\forall y_2\in Y_2$，有 $y_2$ 总是 $X$ 的极限点，自然可以对应一个序列 $\set{x_n}\to y_2$ 进而对应一个 $Y_1$ 中点 $y_1$，即有 $f(y_1)=y_2$

接下来我们证明 $f$ 是保度量的，即 $d_2(f(y_1'),f(y_1''))=d_1(y_1',y_1''),\forall y_1',y_1''\in Y_1$.

如果 $y_1',y_1''\in X$，等式是平凡的；

否则，我们能找到 $\set{x_n'},\set{x_n''}$，使得 $x_n'\to y_1',x_n''\to y_1''$.

由刚才的引理，有 $d_1(y_1',y_1'')=\lim_{n\to\infty} d_1(x_n',x_n'')$. 我们记这个式为式 (1)；

同理，令 $y_2'=f(y_1'),y_2''=f(y_1'')$，由 $f$ 的定义有 $x_n'\to y_2',x_n''\to y_2''$ 于 $(Y_2,d_2)$

于是 $d_2(y_2',y_2'')=\lim_{n\to\infty}d_2(x_n',x_n'')$

因此 $d_2(y_2',y_2'')=d_1(y_1',y_1'')$，因此映射 $f$ 保度量。

由于若 $y_1'\neq y_1''$，$d_2(f(y_1'),f(y_1''))=d_1(y_1',y_1'')>0$，因此 $f$ 是单射，因此 $f$ 双射且保度量，因此 $(Y_1,d_1),(Y_2,d_2)$ 是 Isometric 的。
度量空间完备化的存在性 (Existence of Completion)

定理：如果我们将两个 Isometric 的空间等同起来（看成是同一个空间），则所有的度量空间都有完备化。

证明：令 $(X,d_X)$ 是一个度量空间，考虑 $\set{x_n'},\set{x_n''}$ 是两个柯西序列。称这两个柯西序列是等价的如果 $\lim_{n\to\infty}d_X(x_n',x_n'')=0$。可以验证，这样的定义定义了一个等价关系。

令 $S$ 是所有 $X$ 中柯西序列的等价类构成的集合，定义度量 $d$：

考虑 $s',s''\in S$，分别取代表元 $\set{x_n'},\set{x_n''}$，定义 $d(s',s'')=\lim_{n\to\infty} d_X(x_n',x_n'')$. 由之前的引理，该极限存在因为其是一个实数集中的柯西序列，并且该极限确实不依赖于代表元的选取。

于是 $(S,d)$ 确实是一个度量空间。我们希望将 $(X,d_X)$ 嵌入到 $(S,d)$ 中.

考虑嵌入映射：考虑嵌入 $i:x\to\set{x_n=x}$ 常数序列，则 $(X,d_X)$ 与其像 $(i(X),d|_{i(X)})$ 是 isometric 的。

我们证明 $(S,d)$ 是 $(i(X),d|_{i(X)})$ 的完备化：

令 $s\in S,\set{x_n}$ 是 $s$ 的代表元，则 $\set{i(x_n)}$ 是一个 $i(X)$ 中序列。我们有 $d(i(x_n),s)=\lim_{m\to\infty} d_X(x_n,x_m)$

因此 $\lim_{n\to\infty} d(i(x_n),s)=\lim_{n\to\infty}\lim_{m\to\infty} d_X(x_n,x_m)=0$

于是若 $s\not\in i(X)$，则 $s$ 是 $i(X)$ 的极限点。因此 $\overline{(i(X))}=S$

最后，我们只需证明 $S$ 是完备的。

根据定义，找柯西列 $\set{s_n}$，由于 $\overline{i(X)}=S$，我们总可以找到一些 $\xi_n\in i(X),\forall n$，使得 $d(\xi_n,s_n)<\cfrac{1}{n}$. 于是 $\set{\xi_n}$ 是一个柯西列，因为 $d(\xi_n,\xi_m)\leq d(\xi_n,s_m)+d(s_n,s_m)+d(s_m,\xi_m)$.

令 $\xi_n=i(x_n)$，有 $\set{x_n}$ 是柯西序列，则 $\set{x_n}$ 所在的等价类为 $s\in S$.

我们考虑证明 $s_n\to s$.

有 $d(s,s_n)=\lim_{m\to\infty}(\xi_m,s_n)<\lim_{m\to\infty}(d(\xi_m,\xi_n)+\cfrac{1}{n})$

于是 $\lim_{n\to\infty} d(s,s_n)=0$，于是 $(S,d)$ 完备。

05. 紧空间与Hausdorff空间

紧空间 (Compactness)

数学分析时的紧空间
- 闭区间的有限覆盖定理 (Heine-Borel Theorem)
  考察闭区间 $I=[a,b]\subseteq \mathbb R$，考虑开覆盖 $I\subset \bigcup_\alpha U_\alpha$，其中 $U_\alpha$ 是 $\mathbb R$ 中开集。则其中存在有限多个开集 $U_1,U_2,\cdots,U_n\in \set{U_\alpha}$，使得 $I\subset \bigcup_{i=1}^n U_i$.
紧空间 (Compact Space)

令 $X$ 是一个一般拓扑空间，把 $X$ 称作一个紧空间 (Compact)，如果任意一个开覆盖 $X=\bigcup_{\alpha}U_\alpha$，$U_\alpha\subset X$ 为开，则 $\exists U_1,\cdots,U_n\in \set{U_\alpha}$，使得 $X=\bigcup_{i=1}^n U_i$.
紧集 (Compact Set)

$A\subset X$ 是一个子集，把 $A$ 称作是一个紧子集 (Compact Set)，如果 $A$ 装备上子空间拓扑后是紧空间。

运用如上的概念，可以知道先前的有限覆盖定理说的就是：$\mathbb R$ 中的闭区间是紧子集。

最终，我们希望证明下面的主定理：
欧氏空间中的紧集（主定理）

$X\subset \mathbb R^n$ 是一个紧集，当且仅当 $X$ 是一个有界闭集。
紧集的简单性质
- 连续映射保持紧性
  
  考虑连续映射 $f:X\to Y$，如果 $X$ 是紧空间，则 $f(X)$ 是 $Y$ 中的紧子集。
  
  证明：
  
  令 $f(X)\subseteq \bigcup_\alpha V_\alpha$，其中 $V_\alpha$ 是 $Y$ 中开集 $\forall \alpha$. 根据 $f$ 是连续的，有 $f^{-1}(V_\alpha)$ 是开集。
  
  因为 $X$ 是紧空间，且 $X=\bigcup_\alpha f^{-1}(V_\alpha)$，因此 $\exists V_1,\cdots,V_n\in\set{V_\alpha}$，使得 $X=\bigcup_{i=1}^n f^{-1}(V_i)$，进而 $f(X)\subseteq \bigcup_{i=1}^n V_i$.
  
  由于一开始取的覆盖是任意的，我们得到 $f(X)$ 是一个紧集。
- 闭子集保持紧性
  
  $C\subseteq X$ 是一个闭集。则若 $X$ 是一个紧空间，$C$ 是一个紧子集。
  
  证明：
  
  令 $C\subseteq \bigcup_{\alpha} U_\alpha$，其中 $U_\alpha$ 是 $X$ 中开集 $\forall \alpha$. 由于 $C$ 是闭集，则 $X\setminus C$ 是开集。
  
  于是 $X=\bigcup_{\alpha}U_\alpha \cup (X\setminus C)$，这是一个开覆盖，由于 $X$ 是紧的，因此 $\exists U_1,\cdots,U_n\in\set{U_\alpha}$，使得 $X=\bigcup_{i=1}^n U_i\cup (X\setminus C)$.
  
  进而 $C\subseteq \bigcup_{i=1}^n U_i$，于是由取覆盖的任意性，有 $C$ 是一个紧集。
Hausdorff 空间

称拓扑空间 $X$ 是 Hausdorff 空间，如果对于 $\forall x_1,x_2\in X,x_1\neq x_2$，$\exists$ 邻域 $U_1,U_2$，有 $x_1\in U_1,x_2\in U_2$，使得 $U_1\cap U_2=\varnothing$.
- 例子
  
  若 $(X,d)$ 是一个度量空间，则它是一个 Hausdorff 空间。
  
  $\forall x_1\neq x_2\in X$，有 $d(x_1,x_2)=a>0$. 于是 $B(x_1,\cfrac{a}{4})\cap B(x_2,\cfrac{a}{4})=\varnothing$ 且它们分别是 $x_1,x_2$ 的邻域，于是 $(X,d)$ 是 Hausdorff 空间。
  
  考虑 $\mathbb C$ 上的 Zariski Topology （有限补拓扑），则 $\mathbb C$ 不是一个 Hausdorff 空间。
  
  根据定义，$\forall x_1\neq x_2\in\mathbb C$，令 $U_1,U_2$ 是 $x_1,x_2$ 的两个邻域，则 $\mathbb C\setminus U_1$ 与 $\mathbb C\setminus U_2$ 都是有限集，它们不可能无交，$U_1\cap U_2\neq\varnothing$。于是 $\mathbb C$ 上的 Zariski Topology 不是一个 Hausdorff 空间。
- Hausdorff 空间的极限存在则唯一
  
  如果 $f:X\to Y$ 是一个从集合 $X$ 到 Hausdorff 空间 $Y$ 的映射。令 $\beta$ 是 $X$ 的一组基，如果 $\lim_\beta f(x)$ 存在，则极限唯一。
  
  证明：
  
  假设 $\exists y_1\neq y_2\in Y$，使得 $y_1,y_2$ 都是 $f$ 关于基 $\beta$ 的极限。
  
  于是 $\exists V_1$ 与 $V_2$ 是 $y_1$ 与 $y_2$ 的邻域，使得 $V_1\cap V_2=\varnothing$.
  
  根据极限的概念，$\exists B_1,B_2\in \beta$，使得 $f(B_1)\subset V_1,f(B_2)\subset V_2$，进而 $\exists B_3\subset B_1\cap B_2, B_3\in \beta$，使得 $f(B_3)\subset V_1,f(B_3)\subset V_2$ 且 $B_3\neq\varnothing$（由于基的性质），这样的 $B_3$ 不存在，矛盾！
  
  于是极限一定唯一。
- 度量空间点列极限的叙述
  
  令 $X=\set{1,2,3,\cdots}$，$Y$ 是一个 Hausdorff 空间。令 $\beta=\set{\set{n,n+1,n+2,\cdots}\mid n \geq 1}$，则 $\beta$ 是 $X$ 的一组基，记作 $n\to\infty$.
  
  令 $f:X\to Y$ 是一个映射，将 $f(n)$ 记作 $X_n$，则 $\lim_{n\to\infty} X_n:=\lim_{\beta}f(n)$. 若该极限存在，则该极限唯一。
- Hausdorff 空间与紧集
  
  Haudorff 空间中的紧子集为闭集。
  
  证明：令 $X$ 是一个 Hausdorff 空间，令 $A\subseteq X$ 是一个紧子集.
  
  令 $x\in X\setminus A$，对 $\forall z\in A$，$\exists$ 邻域 $x\in U_z$ 与 $z\in V_z$，使得两个邻域不相交。
  
  于是 $A\subseteq \bigcup_{z\in A} V_z$. 由于 $A$ 是一个紧集，$\exists z_1,\cdots,z_n\in A$，使得 $A\subseteq \bigcup_{i=1}^n V_{z_i}$.
  
  令 $U_x=\bigcap_{i=1}^n U_{z_i}$，有 $U_x\cap A=\varnothing$，并且 $U_x$ 是 $x$ 的一个邻域。
  
  于是 $X\setminus A=\bigcup_{x\in X\setminus A} U_x$ 是一个开集，于是 $A$ 是一个闭集。
连续双射与同胚

回忆：若 $f:X\to Y$ 连续双射，然而 $f$ 不一定是一个同胚映射（线段打到圆）。

定理：考虑 $f:X\to Y$ 连续双射，若假设 $X$ 是紧空间，并且 $Y$ 是一个 Hausdorff 空间，则 $f$ 一定是同胚。

证明：任取 $A\subseteq X$ 是闭集，$X$ 是紧的，有 $A$ 也是紧的，于是 $f(A)$ 在 $Y$ 中是紧的，于是 $f(A)$ 在 $Y$ 中是闭集（$Y$ 是 Hausdorff），于是 $f^{-1}$ 是连续映射，于是 $f$ 是同胚。
紧空间中无限集必有极限点

考虑紧空间中的无限集，这个无限集一定有一个极限点。（回忆：有界数列必有收敛子列）

证明：

令 $X$ 是紧空间，令 $S\subseteq X$ 是一个没有极限点的子集。我们接下来证明 $S$ 是一个有限集，即 $|S|<\infty$。

$\forall x\in X$，$\exists$ 邻域 $x\in U_x$，使得 $U_x\cap S=\begin{cases}\varnothing&x\not\in S\\\set{x}&x\in S\end{cases}$

由于 $X$ 是紧的，$\exists x_1,\cdots x_n\in X$，使得 $X=\bigcup_{i=1}^n U_{x_i}$.

由于每个 $U_{x_i}$ 至多包含了 $S$ 中的一个点，有 $S$ 是一个有限集。
主定理的证明，必要条件

若 $A\subseteq \mathbb R^n$，并且 $A$ 是紧的，则 $A$ 是有界闭集。

证明：

$\mathbb R^n$ 是一个 Hausdorff 空间，于是 $A$ 是闭集；

考虑开球族 $B(0,m),m=1,2,3,\cdots$，我们知道 $A\subset \bigcup_{m=1}^{\infty}B(0,m)$，由于 $A$ 是紧集，于是$\exists k$，使得 $A\subset \bigcup_{m=1}^k B(0,m)$.

于是 $A\subset B(0,k)$，于是 $A$ 有界。
紧集与函数极值

考虑映射 $f:X\to\mathbb R$，它是一个连续映射。则若 $X$ 是一个紧空间，则 $f$ 有最大值与最小值（$f$ 有界且 $f$ 可以取到边界）。

证明：

$X$ 是紧空间，于是 $f(X)$ 是 $\mathbb R$ 中紧子集，于是根据主定理的必要性，有 $f(X)$ 是有界闭集。因此 $f$ 是有界函数。

更多地，因为 $f(X)$ 是闭集，$f(X)$ 包含了自身的所有极限点，于是 $f$ 的最大最小值（边界）都可以取到。
Lebesgue 引理 (Lebesgue's Lemma)

令 $X$ 是一个紧的度量空间，令 $X=\bigcup_\alpha U_\alpha$ 是 $X$ 的开覆盖。则 $\exists \delta>0$，将 $\delta$ 称作关于 $X$ 的开覆盖 $\set{U_\alpha}$ 的 Lebesgue 数 (Lebesgue Number)，使得 $\forall X$ 的子集，若其直径小于 $\delta$，则其一定被包含在某一个 $U_\alpha$ 里。（直径 (Diameter)：$A$ 的直径被定义为 $\sup_{x_1,x_2\in A} d(x_1,x_2)$）

证明：

反证法，假设 $\exists A_1,A_2,\cdots$，$A_i\subseteq X$，使得 $A_i$ 的直径 $\xrightarrow{i\to\infty} 0$，且 $A_i$ 均不被包含在任意一个 $U_\alpha$ 中。

$\forall i$，选取 $x_i\in A_i$. 考虑点列 $\set{x_i}$.

若该点列是一个有限集，则 $\exists k_1<k_2<k_3<\cdots$，使得 $x_{k_1}=x_{k_2}=\cdots$. 令 $p=x_{k_1}$.

否则，$\set{x_i}$ 是一个无限集，其一定有一个极限点，记作 $p$.

不管是哪种情况，总有 $\exists \alpha,p\in U_\alpha$. 于是 $\exists \varepsilon>0$，使得 $B(p,\varepsilon)\subset U_\alpha$.

我们选取足够大的 $N$，使得 $A_N$ 的直径小于 $\cfrac{\varepsilon}{2}$ 并且 $x_N\in B(p,\cfrac{\varepsilon}{2})$.

然而在此种情况下 $\forall x\in A_N$，$d(x,p)\leq d(x,x_N)+d(x_N,p)<\varepsilon$.

于是 $A_N\subset B(p,\varepsilon)\subseteq U_\alpha$，矛盾！
乘积拓扑 (Product Topology)

$X$ 和 $Y$ 是两个拓扑空间，问：能否在 $X\times Y$ 上定义一个自然的拓扑结构？

考察 $U\times V$，其中 $U$ 是 $X$ 中开集，$V$ 是 $Y$ 中开集，我们可以将 $U\times V$ 定义为 $X\times Y$ 中的开集吗？答案是不行的，因为 $U_1\times V_1 \cup U_2\times V_2$ 未必能长成乘积的形式。

例子：$\mathbb R^2=\mathbb{R\times R}$. $U\subset \mathbb R^2$ 为开圆盘，其自然不形如 $V_1\times V_2$，其中 $V_1,V_2$ 是 $\mathbb R$ 中开集，但 $U$ 是开集。（在这里，$U$ 可以是开圆盘）

然而，若设 $\beta=\set{U\times V\mid U,V\subset \mathbb R,U,V \text{开}}$，有 $\beta$ 可以是 $\mathbb R^2$ 的一组拓扑基。

我们来引出一个一般的乘积拓扑概念：

令 $X,Y$ 是拓扑空间，令 $\beta=\set{U\times V\mid U\subset X,V\subset Y,\text{开集}}$. 我们在 $X\times Y$ 上装备拓扑，使得其以 $\beta$ 作为一组基，这样装备的拓扑称作是乘积拓扑 (Product Topology).

装备了乘积拓扑的乘积空间 $X\times Y$ 称作是乘积空间 (Product Space).

注：

良定义的证明：$U_1\times V_1\cap U_2\times V_2=(U_1\cap U_2)\times (V_1\cap V_2)\in \beta$. 于是 $\beta$ 确实可以定义一个拓扑。

回忆：令 $X$ 是一个集合，令 $\beta$ 是 $X$ 中集族且 $\beta$ 不为空，假设 $\bigcup_{B\in\beta}B=X$ 且 $\forall B_1,B_2\in \beta$，$\forall x\in B_1\cap B_2$，$\exists B_{3}^{x}\in \beta$，使得 $x\in B_{3}^x$ 且 $B_{3}^x\subset B_1\cap B_2$，则我们可以定义 $X$ 中开集为 $\beta$ 中成员的任意并，则这个定义给出了 $X$ 上的一个拓扑。
- 乘积空间的投影映射
  
  考虑 $X\times Y$，其自然会诱导两个投影映射 $p_1:X\times Y\to X, p_2:X\times Y\to Y$.
  
  其中 $p_1(x,y)=x,p_2(x,y)=y$，我们将 $p_1,p_2$ 称为投影映射。
- 乘积拓扑关于投影的最小性
  
  乘积拓扑是使得 $p_1,p_2$ 是连续映射的最小拓扑。（最小：包含开集数量“最小”）
  
  证明：
  
  首先证明，如果我们装备了乘积拓扑，则 $p_1,p_2$ 连续。
  
  任取 $U\subset X$ 是开集，则 $p_1^{-1}(U)=U\times Y\subset X\times Y$ 中开集，因此 $p_1$ 是连续的；
  
  类似地 $p_2$ 也是连续的。
  
  反过来，如果我们在 $X\times Y$ 上装备了某一拓扑使得 $p_1,p_2$ 是连续的，则 $p_1^{-1}(U)\cap p_2^{-1}(V)=U\times V$. 这是一个开集若 $U\subset X,V\subset Y$ 是开集。
  
  于是在这个拓扑一定包含了乘积拓扑中的所有基础开集。根据定义，它包含了乘积拓扑中的所有开集，于是乘积拓扑满足这个“最小性”。

06. 乘积拓扑与连通性入门

乘积拓扑 (Product Topology)

定义

$X\times Y$ 上定义乘积拓扑，我们找到 $\beta=\set{U\times V\mid U\subseteq X, V\subseteq Y, U, V\text{ open}}$，则令 $\beta$ 作为拓扑基，这给出了乘积拓扑。

投影映射：

$p_1:X\times Y\to X, p_2:X\times Y\to Y$.

其中 $p_1(x,y)=x,p_2(x,y)=y$，我们将 $p_1,p_2$ 称为投影映射。

我们已经证明了投影映射是连续的，且乘积拓扑是使得投影映射连续的最小拓扑。
像为乘积拓扑映射的连续性

映射 $f:Z\to X\times Y$ （今后若不做特殊说明，则默认 $X\times Y$ 装备乘积拓扑），映射是连续映射当且仅当 $p_1\circ f$ 与 $p_2\circ f$ 都是连续映射。

证明：

$(\Rightarrow)$: 由于 $p_1,p_2,f$ 都是连续的，自然映射的复合也是连续的。

$(\Leftarrow)$: 由连续的定义，取 $U\times V\subset X\times Y$，使得这是一个基础开集。（回忆，如果所有基础开集的原像都是开集，则映射是连续的）

我们考察 $f^{-1}(U\times V)=(p_1\circ f)^{-1}(U)\cap (p_2\circ f)^{-1}(V)$，这自然是一个开集，因此 $f$ 是连续的。
乘积拓扑保持 Hausdorff

若 $X,Y\neq\varnothing$ 是两个拓扑空间，则 $X\times Y$ 是 Hausdorff 的当且仅当 $X,Y$ 都是 Hausdorff 的。

证明： $(\Rightarrow)$: 任取 $x_1\neq x_2\in X$，我们选取 $y\in Y$，于是存在邻域 $(x_1,y)\in U_1\times V_1,(x_2,y)\in U_2\times V_2$ 两个邻域，使得 $(U_1\times V_1)\cap (U_2\times V_2)=\varnothing$（任何开集都可以写成基础开集的并形式，因此一定能取出基础开集）。

由于 $y\in V_1\cap V_2$，我们有 $U_1\cap U_2=\varnothing$，因此 $X$ 是 Hausdorff，类似地 $Y$ 也是 Hausdorff.

$(\Leftarrow)$: 我们令 $(x_1,y_1)\neq(x_2,y_2)$，不妨设 $x_1\neq x_2$，则 $\exists U_1,U_2$ 是 $x_1,x_2$ 邻域，使得 $U_1\cap U_2=\varnothing$.

于是 $U_1\times Y$ 与 $U_2\times Y$ 是 $(x_1,y_1)$ 以及 $(x_2,y_2)$ 的邻域，且它们的交为空。于是 $X\times Y$ 是 Hausdorff.
验证紧性可只取基础开集

令 $\beta$ 是 $X$ 的一个拓扑基，则 $X$ 是一个紧空间，当且仅当对于任意的开覆盖 $X=\bigcup_{\alpha}B_\alpha$，其中 $B_\alpha$ 都是基础开集，都 $\exists B_1,\cdots,B_n\in \set{B_\alpha}$，使得 $X=\bigcup_{i=1}^n B_i$.

证明：只需要验证右推左

$(\Leftarrow)$: 令 $X=\bigcup_{\alpha} U_\alpha$ 是一个任意开覆盖，则 $\forall \alpha$，$U_\alpha=\bigcup_{\gamma\in I_\alpha} B_\gamma$，其中 $B_\gamma\in \beta$，$I_\alpha$ 为指标集。

于是 $X=\bigcup_\alpha\bigcup_{\gamma\in I_\alpha}B_\gamma$.

于是 $\exists B_1,\cdots,B_n\in \beta$，使得 $X=\bigcup_{i=1}^n B_i$.

我们选取 $U_i$ 使得 $B_i\subset U_i$，于是 $X=\bigcup_{i=1}^n U_i$.

于是 $X$ 是紧的。
乘积拓扑保持紧性

令 $X,Y\neq\varnothing$，则 $X\times Y$ 是紧的当且仅当 $X,Y$ 都是紧的。（注：不是空集是必要的，否则任何集合乘空集都是紧集，上面同）

证明：

$(\Rightarrow)$: 令 $p_1:X\times Y\to X,p_2:X\times Y\to Y$ 是投影映射，则 $X=p_1(X\times Y)$，$Y=p_2(X\times Y)$.

我们知道 $p_1,p_2$ 是连续映射，$X\times Y$ 是紧的，自然有 $X,Y$ 都是紧的。

$(\Leftarrow)$: 令 $X\times Y=\bigcup_{\alpha} U_\alpha\times V_\alpha$ 开覆盖。

$\forall x\in X$，考虑 $p_2|_{\set x\times Y}=\set x\times Y\to Y$，这是一个同胚映射，因此 $\set x\times Y$ 是一个紧空间。

于是 $\exists U_1^x\times V_1^x,\cdots,U_{n_x}^x\times V_{n_x}^x\in \set{U_\alpha\times V_\alpha}$，使得 $\set x\times Y\subseteq\bigcup_{i=1}^{n_x} U_i^x\times V_i^x$.

令 $U^x=\bigcap_{i=1}^n U_i^x$，于是 $U^x\times Y\subseteq \bigcup_{i=1}^{n_x} U_i^x\times V_i^x$.

我们对所有 $x\in X$ 找 $U^x$，则 $X=\bigcup_x U^x$.

由于 $X$ 是紧的，于是 $\exists x_1,\cdots,x_n\in X$，使得 $X=\bigcup_{i=1}^n U^{x_i}$.

于是 $X\times Y=\bigcup_{i=1}^{n}U^{x_i}\times Y$.

于是 $X\times Y=\bigcup_{i=1}^n\bigcup_{j=1}^{n_{x_i}} U_j^{x_i}\times V_j^{x_i}$，于是 $X\times Y$ 为紧集。
主定理的证明，充分条件

回忆主定理：$X\subset \mathbb R^n$ 是一个紧集，当且仅当 $X$ 是一个有界闭集。

充分条件：若 $X\subset \mathbb R^n$，且 $X$ 是有界闭集，则 $X$ 是一个紧集。

证明：由于 $X$ 是有界的，因此 $\exists M>0$，使得 $X\subseteq [-M,M]^n$.

由闭区间的有限覆盖定理，$[-M,M]$ 是紧集；由乘积拓扑保持紧性，有 $[-M,M]^n$ 也是紧集。

由于 $X$ 是闭集，于是 $X\subseteq [-M,M]^n$ 是闭集；由于闭子集保持紧性，有 $X$ 在 $[-M,M]^n$ 是紧集，其在 $\mathbb R^n$ 中也是紧集。
*无穷乘积 (Infinite Product)

考虑集合的乘积 $\prod_{i\in I}X_i$，$|I|$ 可以是 $\infty$.

问题：如何在 $\prod_{i\in I}X_i$ 上面定义乘积拓扑？
- 箱拓扑 (Box Topology)
  
  想法1：是否可以按照有限的情形推广构造？
  
  令 $\beta=\set{\prod_{i\in I}U_i\mid U_i\subset X_i\text{ open}}$，$\beta$ 确实可以定义一个拓扑，使得 $\beta$ 是一个拓扑基。
  
  这样构造出的拓扑我们称之为箱拓扑 (Box Topology).
- 乘积拓扑 (Product Topology)
  
  想法2：我们只在有限多的分量中取开集会如何？
  
  令 $\beta=\set{U_{i_1}\times U_{i_2}\times\cdots\times U_{i_k}\times \prod_{i\in I\setminus\set{i_1,i_2,\cdots,i_k}}\mid k\geq 0,i_1,\cdots,i_k\in I,U_{i_j}\subset X_{i_j}\text{ open}}$，可以验证 $\beta$ 也定义了一个拓扑，使得 $\beta$ 是一个拓扑基。
  
  我们将这个拓扑称为无穷乘积情况下的乘积拓扑 (Product Topology).
- 两种拓扑的差异
  
  当 $|I|<\infty$，两个拓扑完全等价。
  
  我们会有如下定理：
  - 若 $X_i$ 均为 Hausdorff 空间，则 $\prod_{i\in I}X_i$ 在箱拓扑和乘积拓扑下都是 Hausdorff 空间。
  - 令 $f:Y\to \prod_{i\in I} X_i$，令 $\prod_{i\in I} X_i$ 装备上乘积拓扑，则 $f$ 是连续的当且仅当 $f$ 的每一个分量都是连续的（$\pi_i \circ f$ 均为连续，$\pi_i:\prod_{i\in I} X_i\to X_i$）。
    
    注：如果我们此时装备了箱拓扑，并且假设每一个分量 $\pi_i\circ f$ 都是连续映射，则一般情况下 $f$ 可以不是连续映射。
    
    例如：令 $I=\mathbb N$，令 $X_i=\mathbb R$，$Y=\mathbb R$. 定义映射 $f:\mathbb R\to \prod_{i\in \mathbb N}\mathbb R$，$f(x)=(x,x,x,\cdots)$. 此时有 $\pi_i\circ f=id$，因此每个分量都是连续映射.
    
    然而，找开集 $U=(-1,1)\times (-\cfrac{1}{2},\cfrac{1}{2})\times (-\cfrac{1}{3},\cfrac{1}{3})\times \cdots$，这在箱拓扑中是开集（在乘积拓扑中不是）。而 $f^{-1}(U)=\set{0}$，这不是开集，因此 $f$ 不是连续映射。
  - 吉洪诺夫定理 (Tychonoff Theorem)
    
    若 $X_i$ 是紧集，则 $\prod_{i\in I}X_i$ 在乘积拓扑下也是紧的。
    
    注：在箱拓扑下这个结论是错误的。

连通性 (Connectedness)

两种关于连通性的观点
- 集合划分观点
  
  $X$ 被称为是连通的，当且仅当若 $X=A\cup B$ 且 $A,B\neq \varnothing$，则 $\bar A\cap B\neq\varnothing$ 或 $A\cap \bar B\neq\varnothing$.
  
  如图，在这种情况下，中间的“线”会在某个集合取闭包后被两个集合同时包含。
- 道路连通观点
  
  令 $I=[0,1]$ 区间，$X$ 是连通的当且仅当 $\forall p,q\in X$，$\exists$ 连续映射 $f:[0,1]\to X$，使得 $f(0)=p,f(1)=q$.
- 两种观点的整理
  
  最终，我们会将第一种观点称作连通性 (Connectedness)，将第二种观点称作 道路连通性 (Path-Connectedness)。
  
  我们将会证明道路连通性$\Rightarrow$连通性，但一般情况下，连通性$\not\Rightarrow$道路连通性。
连通性的定义 (Connectedness)

拓扑空间 $X$ 被称为是连通的，如果 $\forall A,B\neq \varnothing$，使得 $X=A\cup B$，总有 $A\cap \bar B\neq \varnothing$ 或 $\bar B\cap A\neq\varnothing$.
连通性的等价条件

下面几个关于连通性的条件是等价的：
- $(1)$ $X$ 是连通的（定义）；
- $(2)$ $X$ 中既开又闭的集合只有 $X$ 与 $\varnothing$；
- $(3)$ $X$ 不能被表示为两个非空开集的不交并。
证明：

$(1)\Rightarrow(2)$: 任取 $A\in X$ 是既开又闭的，取 $B=X\setminus A$，自然 $B$ 也是既开又闭的。有 $A=\bar A,B=\bar B$，且 $\bar A\cap B=A\cap \bar B=\varnothing$，$X=A\cup B$.

此时由 $(1)$，总有 $A=\varnothing$ 或者 $B=\varnothing$，因此 $A=X$ 或 $A=\varnothing$.

$(2)\Rightarrow(3)$: 令 $X=A\cup B$，其中 $A,B$ 为开集且 $A=X\setminus B$.

此时 $A,B$ 也都是闭集，由于 $(2)$，有 $\set{A,B}=\set{X,\varnothing}$，因此得出结论。

$(3)\Rightarrow(1)$: 令 $X=A\cup B$，其中 $A,B\neq\varnothing$.

假设 $\bar A\cap B=\varnothing=A\cap \bar B$，因此 $A\cap B=\varnothing$ 且 $X=A\sqcup B=\bar A\sqcup B=A\sqcup \bar B$，于是 $A=\bar A,B=\bar B$. （注：$A\sqcup B$ 表示 $A$ 与 $B$ 的不交并）

于是 $A,B$ 又分别是开集，由于 $(3)$，矛盾！
实数轴是连通的

$\mathbb R$ 是连通的。

证明：假设 $\mathbb R=A\cup B$ 且 $\bar A\cap B=A\cap\bar B=\varnothing$，则有 $A\cap B=\varnothing$.

假设 $A,B\neq \varnothing$，选取 $a\in A,b\in B$，不妨设 $a<b$.

考虑集合 $X=\set{x\in A\mid x<b}$，令 $s$ 是 $X$ 的上确界。

如果 $s\in A$，有 $s=\max X$，且 $s<b$，此时 $(s,b]\subseteq B$，于是 $s\in \bar B\cap A$，与假设矛盾；

如果 $s\in B$，有 $s\not\in A$，但 $s=\sup X$，于是 $s\in \bar A\cap B$，与假设矛盾。

综上，假设不成立，有 $\mathbb R$ 是连通的。
连续映射保持连通性

考虑 $f:X\to Y$ 连续映射，且 $X$ 是连通的，则像 $f(X)$ 也是连通的。

证明：令 $f(X)=A\cup B$，其中 $A,B$ 是 $f(X)$ 中开集且 $A\cap B=\varnothing$.

此时有 $X=f^{-1}(A)\cup f^{-1}(B)$，自然有 $f^{-1}(A),f^{-1}(B)$ 是 $X$ 中开集且 $f^{-1}(A)\cap f^{-1}(B)=\varnothing$.

于是有 $f^{-1}(A)=\varnothing$ 或 $f^{-1}(B)=\varnothing$，于是 $A=\varnothing$ 或 $B=\varnothing$，因此 $f(X)$ 是连通的。

我们有如下的自然推论：令 $h:X\to Y$ 为同胚，则 $X$ 是连通的当且仅当 $Y$ 是连通的。
取闭包保持连通性

令 $X$ 是一个拓扑空间，$Z\subseteq X$ 且稠密。则若 $Z$ 是连通的，则 $X$ 是连通的。

证明：令 $\varnothing \neq A\subseteq X$ 且既开又闭，由于 $\bar Z=X$ 且 $A$ 是开集，我们有 $Z\cap A\neq \varnothing$.

于是有 $Z\cap A$ 是 $Z$ 中既开又闭的集合且是非空的，由连通性，有 $Z\cap A=Z$，于是 $Z\subset A$.

于是 $X=\bar X\subset \bar A=A$，于是 $X=A$，于是 $X$ 连通。

07. 连通性与道路连通性

连通性 (Connectedness)

回顾：闭包维持连通性

若 $Z\subseteq X$ 是稠密的且 $Z$ 是连通的，则 $X$ 是连通的
介于连通集合与其闭包间的集合也连通

若 $Z\subseteq X$，$Z$ 是连通的且 $Z\subseteq Y\subseteq \overline Z$，则 $Y$ 是连通的。特别地，若取 $Y=\overline Z$，即有 $\overline{Z}$ 连通。

证明：在 $Y$ 中取 $Z$ 的闭包即为 $Y$，由闭包维持连通性立得。
$\mathbb{R}$ 中的连通集合为区间

$\varnothing\neq X\subseteq\mathbb{R}$，则 $X$ 是连通的当且仅当 $X$ 是区间。

证明：$(\Rightarrow):$ 假设 $X$ 不是一个区间，则 $\exists p\in \mathbb{R}\setminus X$，使得 $\exists a,b\in X$，有 $a<p<b$.

令 $A=\set{x\in X\mid x < p}$，令 $B=\set{x\in X\mid x>p}$，由刚刚的性质，我们知道这两个集合非空，并且 $X=A\sqcup B$ （$X=A\cup B, A\cap B=\varnothing$）。

我们接下来证明 $A,B$ 均为开集。$\forall x\in A$，$\exists \varepsilon>0$，使得 $x+\varepsilon<p$，于是 $(-\infty, x+\varepsilon)\cap X$ 就是 $x$ 在 $X$ 中邻域，且这个邻域位于 $A$ 中，于是 $A$ 在 $X$ 中为开集。

类似地，我们可以说明 $B$ 在 $X$ 中也为开集，如此我们得到矛盾，$X$ 不是连通。

$(\Leftarrow):$ 考虑开区间 $(a,b)$，其中 $a<b$. 开区间同胚于 $\mathbb{R}$，由于 $\mathbb{R}$ 连通，因此 $(a,b)$ 自然为连通集。

考虑闭区间 $[a,b]$，有 $[a,b]=\overline{(a,b)}$，由上面定理有 $[a,b]$ 连通。

考虑半开半闭区间 $(a,b]$，有 $(a,b)\subseteq (a,b]\subseteq \overline{(a,b)}$，因此 $(a,b]$ 连通。

同理 $[a,b)$ 也连通。

因此区间为连通的。
并集与连通性

Q：考虑两个连通集合 $A,B$ 的并集 $A\cup B$，问 $A\cup B$ 是否连通？

如果不加限制，显然答案是否定的。例如两个不交的圆盘。如何加以限制使得并集也是连通的？
- 相互分离的定义 (Separated)
  
  考虑 $A,B\subseteq X$，我们称 $A,B$ 是相互分离 (separated)的，若 $\overline{A}\cap\overline{B}=\varnothing$.
- 不相互分离集合的并连通
  
  考虑空间 $X=\bigcup_{\alpha} A_\alpha$，其中 $\forall \alpha,A_\alpha$ 是连通的。假设 $\not\exists \alpha_1,\alpha_2$，使得 $A_{\alpha_1}$ 与 $A_{\alpha_2}$ 是分离的（即任意两个成员都不是相互分离的），则 $X$ 是连通的。
  
  证明：
  
  令 $B\subseteq X$ 是既开又闭的集合。由于 $A_\alpha$ 是连通的，$B\cap A_\alpha=\varnothing$ 或 $A_\alpha$. （这是因为 $B\cap A_\alpha$ 是 $A_\alpha$ 中既开又闭的集合）
  
  若 $B\cap A_\alpha=\varnothing,\forall \alpha$，则 $B=\varnothing$.
  
  若 $\exists A_{\alpha_0}\in\set{A_\alpha}$，使得 $B\cap A_{\alpha_0}=A_{\alpha_0}$，于是 $A_{\alpha_0}\subseteq B$.
  
  如果 $\exists A_{\alpha_1}\in\set{A_\alpha}$，使得 $B\cap A_{\alpha_1}=\varnothing$：则由于 $B$ 是一个闭集，有 $\overline{A_{\alpha_0}}\subseteq B$；另一方面，$X\setminus B$ 也是闭集，有 $\overline{A_{\alpha_1}}\subseteq X\setminus B$。于是 $\overline{A_{\alpha_0}}\cap \overline{A_{\alpha_1}}=\varnothing$，矛盾！
  
  因此，$\forall \alpha$，有 $B\cap A_\alpha=A_\alpha$，于是 $B=X$.
  
  进而，$X$ 中既开又闭的集合只有 $X$ 与 $\varnothing$，$X$ 为连通。
- 交集不为空的连通集合族的并连通
  
  如果 $X=\bigcup_{\alpha}A_\alpha$，其中 $\forall \alpha, A_\alpha$ 连通。如果 $\bigcap_{\alpha} A_\alpha\neq\varnothing$，则 $X$ 是连通的。
  
  证明：由上面定理立得。
- 注：取交操作的连通性
  
  若 $A,B\subseteq X$，其中 $A,B$ 都是连通集。问：$A\cap B$ 是否是连通集？
  
  事实上，$A\cap B$ 一般也不是连通集。
  
  如下图：
乘积集合保持连通性

令 $X,Y$ 是非空空间，则 $X\times Y$ 是连通的当且仅当 $X,Y$ 都是连通的。

证明：

$(\Rightarrow):$ 令 $p_1,p_2$ 是两个投影映射，则 $X=p_1(X\times Y)$，根据连续映射保持连通性，有 $X$ 连通；类似有 $Y$ 连通。

$(\Leftarrow):$ $\forall x\in X$，根据 $\set{x}\times Y$ 与 $Y$ 同胚，$Y$ 是连通的，故有 $\set{x}\times Y$ 是连通的。

类似地，$\forall y\in Y$，$X\times \set{y}$ 是连通的。

$(x,y)\in (\set{x}\times Y)\cap (X\times \set{y})$，如果我们定义 $A(x,y):=(\set{x}\times Y)\cup(X\times \set{y})$，有 $A(x,y)$ 是连通的。

我们考虑 $(x',y')\in X\times Y$，考虑 $A(x',y')$，有 $A(x',y')\cap A(x,y)\neq\varnothing$.

因为 $X\times Y=\bigcup_{x\in X,y\in Y}A(x,y)$，这些集合两两不分离。由于先前的定理，有 $X\times Y$ 也是连通的。
$\mathbb{R}^n=\mathbb{R\times R\times\cdots\times R}$ 是连通的

由上面立得。
连通分支的定义 (Connected Components)

对于 $\forall x,y\in X$，定义等价关系 $x\sim y$：$x\sim y$ 如果 $\exists A\subseteq X$，$A$ 是连通的且 $x,y\in A$.

这样定义的等价关系将诱导 $X$ 上的一个等价类，等价类就被称作是 $X$ 的连通分支 (Connected Components)。
- 注：连通分支具有极大性
  
  一个连通分支一定是一个极大的连通子集。
  
  ”极大性“是易于理解的，我们来简单看看连通分支为什么是连通集：令 $A$ 是一个连通分支，我们选择任意的 $x_0\in A$，则 $\forall x\in X$，$\exists B_x$ 连通集合，使得 $x,x_0\in B_x$.
  
  于是 $A=\bigcup_{x\in A} B_x$，因此它是连通的。
- 注：上述关系确实是等价关系
  
  自反性、对称性：这是自然的；
  
  传递性：若 $x\sim y,y\sim z$，则 $\exists A,B$ 连通集，使得 $x,y\in A,y,z\in B$，从而由于 $A\cap B\supset\set{y}\neq \varnothing$，故 $A\cup B$ 连通，故 $x\sim z$.
连通分支是分离的闭集

连通分支是闭集且任意两个不同的连通分支一定是相互分离的。

证明：

闭集：如果 $A\subset X$ 是一个连通分支，有 $A$ 是连通的。于是 $\overline{A}$ 也是连通的。又因为 $A$ 是极大的连通集合，有 $A=\overline{A}$，换言之 $A$ 是闭集。

相互分离：假设 $\exists B$，$B$ 是另一个连通分支，假设 $A,B$ 不是相互分离的。由于 $\overline{A}\cap\overline{B}\neq\varnothing$，有 $A\cup B$ 也是连通集合，这与极大性矛盾。
举例：连通分支

$\mathbb{R}\setminus \set{0}$ 有两个连通分支 $(-\infty,0)$ 与 $(0,+\infty)$。这两个连通分支在 $\mathbb{R}\setminus \set{0}$ 都是既开又闭的。

若 $X$ 只有有限多个连通分支，则这些连通分支均是既开又闭的集合。

考虑有理数集 $\mathbb{Q}$，$\forall x\in \mathbb{Q}$，有 $\set{x}$ 是 $\mathbb{Q}$ 的连通分支。与此同时，$\set{x}$ 在 $\mathbb{Q}$ 中是闭集而不是开集。

令 $X=\set{\cfrac{1}{n}\mid n\geq 1}\cup \set{0}$，则 $\forall x\in X$，有 $\set{x}$ 是连通分支，则 $\set{\cfrac{1}{n}}$ 是既开又闭的，但 $\set{0}$ 只是闭集不是开集。

道路连通 (Path-Connectedness)

道路的定义 (Path)

拓扑空间 $X$ 中的道路 (Path)为一个连续映射 $\gamma:[0,1]\to X$. 将 $\gamma(0)$ 与 $\gamma(1)$ 分别叫做道路的起点 (Beginning Point)以及终点(End Point)。

我们也称 $\gamma$ 是一个连接(join) $\gamma(0)$ 和 $\gamma(1)$ 的道路。
道路连通空间 (Path-Connected Space)

我们称一个空间 $X$ 是道路连通 (Path-Connected)的，如果任意两个点都可以被一个道路连接。
道路连通蕴含连通性

一个道路连通空间 $X$ 一定是连通的。

证明：假设 $X$ 是道路连通的，令 $\varnothing\neq A\subset X$ 使得 $A$ 既开又闭；假设 $A\neq X$.

选取 $x\in A,y\in X\setminus A$，我们可以找到道路 $\gamma$ 连接 $x$ 与 $y$.

考虑 $\gamma^{-1}(A)$，它一定是 $[0,1]$ 中既开又闭的集合，且 $\gamma^{-1}(A)\neq\varnothing,\gamma^{-1}(A)\neq [0,1]$，这与 $[0,1]$ 区间连通矛盾。

因此 $X$ 中既开又闭的集合只有 $X$ 与 $\varnothing$，于是 $X$ 是连通的。
道路连通分支 (Path-Connected Components)

我们可以定义等价关系 $\forall x,y\in X$，定义 $x\sim y$ 若 $\exists$ 道路 $\gamma$ 使得 $\gamma$ 连接了 $x$ 和 $y$.

我们把对应的等价类称作是 $X$ 的道路连通分支 (Path-Connected Components).
- 注：该关系确实是等价关系
  
  自反性：令 $\gamma:[0,1]\to X$，使得 $\gamma(t)=x,\forall t\in [0,1]$，故 $x\sim x$.
  
  对称性：若 $x\sim y$，有 $\exists \gamma$ 道路，使得 $\gamma(0)=x,\gamma(1)=y$，则令 $\alpha:[0,1]\to X,\alpha(t)=\gamma(1-t)$，有 $\alpha$ 连接了 $y,x$，故 $y\sim x$.
  
  传递性：若 $x\sim y,y\sim z$，$\exists \gamma_1,\gamma_2$ 道路，使得 $\gamma_1(0)=x,\gamma_1(1)=y,\gamma_2(0)=y,\gamma_2(1)=z$.
  
  令 $\gamma_3:[0,1]\to X$，$\gamma_3(t)=\begin{cases}\gamma_1(2t)&0\leq t\leq \cfrac{1}{2}\\\gamma_2(2t-1)&\cfrac{1}{2}\leq t\leq 1\end{cases}$.
  
  容易验证 $\gamma_3$ 是连续的（$[0,\cfrac{1}{2}],[\cfrac{1}{2},1]$ 组成了 $[0,1]$ 的闭覆盖，由连续映射的局部性，整体也是连续的）且连接了 $x,z$，故 $x\sim z$.
  
  注：连续映射的局部性：$f:X\to Y$ 是一个连续映射，如果 $X$ 可以表示成一些闭集 $F_i$ 的并，即 $X=\bigcup_{i=1}^n F_i$，且 $f|_{F_i}$ 是连续的。
欧氏空间 $\mathbb{R}^n$ 中连通开集为道路连通

考虑欧氏空间 $\mathbb{R}^n$ 中的一个连通开集，该开集一定是道路连通的。

证明：

令 $X\subset \mathbb{R}^n$ 是一个连通开集。我们固定 $x\in X$，令 $A=\set{y\in X\mid y\text{ 与 }x\text{ 间可以被连接道路}}$；$B=\set{y\in X\mid y\text{ 与 }x\text{ 间不能被连接道路}}$。

因此 $A\cap B=\varnothing$，且 $X=A\cup B$，且 $A\neq\varnothing$。

我们接下来证明 $A,B$ 是开集。$\forall y\in A$，我们总可以选取小球 $B(y,\varepsilon)$，使得 $B(y,\varepsilon)\subseteq X$.

因此 $\forall z\in B(y,\varepsilon)$，总可以将 $z,y$ 间连接一条直线，从而 $z$ 与 $y$ 道路连通。

从而 $z$ 可以与 $x$ 连接道路，于是 $z\in A$.

于是 $A$ 是开集。

类似地，$\forall y\in B$，我们选取小球 $B(y,\varepsilon)\subseteq X$. $\forall z\in B(y,\varepsilon)$，则 $z$ 可以与 $y$ 之间连接一条线段。

于是 $z$ 与 $x$ 之间一定不存在道路，否则 $y$ 与 $x$ 道路连通。于是 $z\in B$.

于是 $B$ 是开集。

于是 $X$ 可以被写成开集 $A,B$ 的不交并，由于 $A$ 不为空，$X$ 连通，有 $B$ 为空。于是 $X$ 道路连通。
反例：连通但不道路连通的集合（拓扑学家的正弦曲线，Topologist's Sine Curve）

令 $Y=\set{(0,y)\in \mathbb{R}^2\mid -1\leq y\leq 1}$，$Z=\set{(x,\sin\cfrac{\pi}{x})\in \mathbb{R}^2\mid 0<x\leq 1}$

我们考察 $X=Y\cup Z$.

注意到 $Z$ 是连通的，由于 $Z=f((0,1])$. $f(x)=(x,\sin \cfrac{\pi}{x})$ 是一个连续函数，因此 $Z$ 也是连通的，并且 $Z$ 是道路连通的；

与此同时，不难注意到 $Y$ 也是道路连通的，然而 $X=Y\cup Z$ 并非道路连通。

进一步地，考察集合 $Z$，有 $X=\overline{Z}$，有 $X$ 也是连通，如此我们给出了一个反例。

注意到 $Z$ 和 $Y$ 即为 $X$ 的道路连通分支，这也告诉我们道路连通分支未必是闭集。

08. 粘合空间

粘合空间 (Identification Spaces)

一些简单的例子

考虑一个圆柱面。$x^2+y^2=1,0\leq z\leq 1,(x,y,z)\in\mathbb{R}^3$

这是圆柱面嵌入到欧氏空间的定义。

考虑将矩形粘合到一起，这也形成了一个圆柱面。

两个圆柱面呈现出什么样的关系呢？我们来研究它们的拓扑结构。不妨来考察圆柱面里的开集，在拉回矩形后就是矩形中的一个小圆形。这意味着圆柱面里的开集在拉回到矩形后仍然是一个开集。

接下来我们考察另一个例子：环面 (Torus)。$X\subseteq \mathbb{R}^3$

能从矩形中构造出环面吗？当然可以。

像是把圆柱面的两头粘在了一起，确实得出了环面。

我们还是来考虑拓扑结构，如下图所示。

此图给出了特殊点的对应关系。（对不起！红绿色盲）

跟圆柱的情形类似，环面的开集拉回矩形后也是开集。

我们将会看到越来越复杂的例子，这会逐渐体现粘合观点的优越性。

我们来看下一个例子：

图中是一根莫比乌斯带 (Mobius Strip)。$X\subseteq \mathbb{R}^3$.

这个图形也可以从矩形粘合得来：

下图给出了它们拓扑结构的关系：

需要注意粘合方法导致两侧半圆不“水平”。

接着来看一个更复杂的例子：

可以考虑先粘上下两边，这得到了一个圆柱面。

粘合左右两边变得没有那么好想象了，下面有一个示意图：

这被称作克莱因瓶 (Klein Bottle)，这个物体不能嵌入欧氏空间。（这个物体事实上可以嵌入四维空间）

最后我们再来看一个例子：

这个物体的示意图变得不那么好画了，但该空间非常重要，我们将它称为 $\mathbb{R}P^2$ 拓扑，实射影平面 (Real Projective Plane).

应该怎么更好地理解它呢？不妨把矩形看作圆盘。

考察圆盘 $B=\set{(x,y)\mid x^2+y^2\leq 1}$

圆周 $S^1=\partial B=\set{(x,y)\mid x^2+y^2=1}$

如何理解上述定义呢？上面的粘合操作等价于，我们将所有的对径点 $P$ 与 $-P$ 粘合起来 $\forall P\in S^1$.

从代数几何视角上看，前两个空间（圆柱、圆环）是可定向曲面，而最后三个空间（莫比乌斯带、克莱因瓶、实射影平面）都是不可定向的。

直观上看，一个可定向的空间可以分出“里面”与“外面”的概念。
粘合拓扑与粘合空间的定义 (Identification Topology / Space)

令 $X$ 是一个拓扑空间，且 $X=\bigsqcup_{i\in I}P_i$ 给出了 $X$ 的一个分划（集合的不交并）。令 $Y=\set{P_i\mid i\in I}$，令 $\pi:X\to Y$，其中 $\pi(x)=P_i\text{ if } x\in P_i$ .

我们在 $Y$ 上装备拓扑，使得 $U\subseteq Y$ 是开集当且仅当 $\pi^{-1}(U)$ 在 $X$ 中是开集。我们将 $Y$ 上的拓扑称为是粘合拓扑 (Identification Topology)，将 $Y$ 称为对应于分划 $\bigsqcup_{i\in I}P_i$ 的粘合空间 (Identification Space)。
以粘合空间重述上面例子

例：考察将矩形粘合成为圆柱面。

将矩形参数化：$X=\set{(x,y)\mid 0\leq x\leq 1,0\leq y\leq 1}$, $Y=\text{圆柱}$.

则 $Y$ 中的点对应 $\set{(x,y)}$ 单点 $(0<x<1)$ 或 $\set{(0,y),(1,y)}$ 这一子集 $(0\leq y\leq 1)$（直观上看，此时点落在“粘合线”上。
粘合空间的泛型 (Universal Property of Identification Space)

令 $Y$ 是一个粘合空间，$\pi:X\to Y$ 是一个粘合映射。令 $Z$ 是另一个拓扑空间。则映射 $f:Y\to Z$ 是连续的，当且仅当 $f\circ \pi:X\to Z$ 是连续的。

如图所示，中间的圆圈形箭头意味着这是一张“交换图表”。

证明：

根据粘合空间的定义，$U\subseteq Z$ 是开集，考虑 $f^{-1}(U)\subseteq Y$，这个集合是开集当且仅当 $\pi^{-1}\circ f^{-1}(U)=(f\circ \pi)^{-1}(U)$ 在 $X$ 中是开集，故定理成立。

这个定理意味着，尽管 $Y$ 经过粘合后往往是个相当复杂的空间，为了判断连续性，我们可以将点“拉回” $X$ 中再去判断。
粘合映射 (Identification Map)

令 $f:X\to Y$ 是一个连续满射。假设 $U\subseteq Y$ 是开的当且仅当 $f^{-1}(U)\subset X$ 是开的，则我们称 $f$ 是一个粘合映射 (Identification Map)。
- 注：由粘合映射导出粘合空间
  
  考虑 $X=\bigsqcup_{y\in Y}f^{-1}(y)$，令 $Y_\star$ 是一个对应于这个分划的粘合空间。于是考虑映射 $h:Y_\star\to Y$，$h(\set{f^{-1}(y)})=y$.
  
  有 $h$ 是一个双射，根据先前粘合映射的定义，我们有 $h$ 是一个同胚。并且我们有一个交换图表：
粘合映射的刻画

令 $f:X\to Y$ 是连续满射，若 $f$ 把 $X$ 中开集映射为 $Y$ 中开集 (开映射，Open Map)，或者 $f$ 把 $X$ 中闭集映射为 $Y$ 中闭集 (闭映射，Close Map)，则 $f$ 是一个粘合映射。

证明：

若 $f$ 是开映射，令 $U$ 是 $Y$ 中集合使得 $f^{-1}(U)\subseteq X$ 是开集。由于 $f$ 是一个满射，于是 $f(f^{-1}(U))=U$，于是 $U$ 是 $Y$ 中开集。于是 $U$ 在 $Y$ 中是开集当且仅当 $f^{-1}(U)$ 在 $X$ 中是开集。故 $f$ 确实是粘合映射。

若 $f$ 是闭映射，证明是类似的。
- 定理的推论
  
  考虑映射 $f:X\to Y$ 是连续满射，假设 $X$ 是紧空间，假设 $Y$ 是 Hausdorff 空间，则 $f$ 是一个粘合映射。
  
  证明：
  
  令 $A \subseteq X$ 是闭集，有 $A$ 是一个紧集。于是 $f(A)$ 在 $Y$ 中也是紧集，由于 $Y$ 是 Hausdorff 空间，因此 $f(A)$ 在 $Y$ 中是闭集，因此 $f$ 是一个闭映射。
  
  于是 $f$ 是粘合映射。
连续映射局部性质的推广 (Generalizatio of local formulation of continuity)

回忆：连续映射的局部刻画：
1. $f:X\to Y$ 是一个连续映射，如果 $X$ 可以被一些开集 $U_\alpha$ 覆盖，即 $X=\bigcup_\alpha U_\alpha$，使得 $f|_{U_\alpha}$ 是连续的。
2. $f:X\to Y$ 是一个连续映射，如果 $X$ 可以表示成一些闭集 $F_i$ 的并，即 $X=\bigcup_{i=1}^n F_i$，且 $f|_{F_i}$ 是连续的。
有了粘合映射的概念后，我们可以如下推广此定理：

令 $X=\bigcup_{\alpha\in I} X_\alpha$，令 $\tilde X=\bigsqcup_{\alpha\in I}X_\alpha$

这事实上是将重复元素”复制”了一份，或者可以记作 $\tilde X=\set{(x,\alpha)\mid \alpha\in I,x\in X_\alpha}$.

在 $\tilde X$ 中装备拓扑：$U\subseteq \tilde X$ 是开集，当且仅当 $U\cap X_{\alpha}$ 是开的，$\forall \alpha$。在这里定义的后半段，$U$ 中的“被复制出的”点又被视为相同点了，或者可以把 $X_\alpha$ 视为 $\set{(x,\alpha)\mid x\in X_\alpha}$。

从而我们定义出了一个新的拓扑空间。

我们令 $j:\tilde X\to X$ 是一个 Canonical Map（$j|_{X_\alpha}:X_{\alpha}\text{ 嵌入映射 }X$），则有如下定理：

考虑映射 $f:X\to Y$ 使得 $f|_{X_\alpha}$ 是连续的，假设 $j:\tilde X\to X$ 是一个粘合映射，则 $f$ 是一个连续映射。

证明：

由于 $j$ 是粘合映射，$f$ 是连续的当且仅当 $f\circ j$ 是连续的。这当且仅当 $f\circ j|_{X_\alpha}$ 是连续的，由上述拓扑空间开集的定义易知其成立。
- 注：定理推广的方式
  考虑 $X=\bigcup_{\alpha} U_\alpha$ 开或 $X=\bigcup_{i=1}^n F_i$ 闭，则 $j:\tilde X\to X$ 都是粘合映射（$j$ 是开映射或闭映射）
粘合映射的例子
- 闭圆盘的粘合
  
  考虑圆盘 Disk $B^2=\set{(x,y)\mid x^2+y^2\leq 1}$，$S^1=\set{(x,y)\mid x^2+y^2=1}$.
  
  考虑粘合映射 $B^2\to X$ 使得该映射把边界圆周 $S^1$ 粘合成了一个点。$X=\set{(x,y)\mid x^2+y^2<1}\cup\set{S^1}$.
  
  我们将 $X$ 记作 $B^2/S^1$（商空间），则 $X$ 同胚于球面 $S^2=\set{(x,y,z)\mid x^2+y^2+z^2=1}$.
  
  更一般地，考虑 $B^n/S^{n-1}$，这是一个粘合空间使得它将边界球面粘合成了一个点（$B^n=\set{x\in \mathbb{R}^n\mid |x|\leq 1},B^n\supseteq S^{n-1}=\set{x\in \mathbb{R}^{n}\mid |x|=1}$），则该空间同胚于 $S^n$.
  
  提示：考虑集合 $B^n\setminus S^{n-1}$，该集合同胚于 $\mathbb{R}^n$. 又考虑 $S^n\setminus \set{p_t}$，其中 $p_t$ 是 $S^n$ 中任意一点，那么这个集合也同胚于 $\mathbb{R}^n$. （球极投影）也就是 $B^n\setminus S^{n-1}\cong \mathbb{R}^n\cong S^n\setminus \set{p_t}$.
- 射影空间 (Projective Space)
  
  我们给出三种构造来构造 $n$ 维的实射影空间 $\mathbb R P^n$，今天我们现在只介绍其中两种：
  
  令 $S^n=\set{x\in \mathbb R^{n+1}\mid |x|=1}\subseteq \mathbb{R}^{n+1}$ 是单位球面，将 $\mathbb{R}P^n$ 定义为粘合空间，它粘合了球面上所有的对径点（也就是把所有 $x,-x,\forall x\in S^n$ 进行粘合）。
  
  以这种方法构造的粘合空间称作 $\mathbb{R}P^n$（$\mathbb{R}P^n=\set{S^n \text{ 中对径点点对构成的集合}}$）。
  
  将 $\mathbb RP^n$ 定义为粘合空间，定义 $\mathbb{R}^{n+1}\setminus\set{0}$ 的一个粘合，我们将所有在同一条通过原点直线上的点粘合在一起，将这个空间称作实射影空间。
  
  如图所示：

09. 拓扑群与矩阵拓扑群

实射影空间 (Real Project Space)

三种构造方法
1. 通过将 $x$ 与 $-x$ 粘在一起构造一个粘合空间，$\forall x\in S^n$；
2. $\mathbb{R}^{n+1}\setminus\set{0}$ 中所有在过原点的同一直线上的点粘合在一起构造一个粘合空间；
3. 令 $B^n$ 是 $n$ 维的单位球，考虑其边界球面，将其对径点粘合在一起，也能构造出实射影空间。（上节课一开始介绍的构造方法）
方法 3 的解释：图中图形同胚于一个 $n+1$ 维半球面，黄色区域可以看成是半球的赤道。

可以看成是上下半球面先粘合，再粘合赤道的对径点。因此方法 3 从直观上看是与方法 1 等价的。
第二种构造方法的推广：复射影平面

注意到第二种构造方法事实上在 $\mathbb{C}^n$ 中也适用，我们将其称之为 $\mathbb{C}P^n$.

考虑粘合空间：$\mathbb{C}^{n+1}\setminus\set{0}$ 中将所有落在同一一维包含原点的线性子空间中的点粘合在一起，则这构成了一个粘合空间，这就构造出了 $\mathbb{C}P^n$.

粘合空间的构造

锥的构造 (Cone)

令 $X$ 是一个拓扑空间，令 $I=[0,1]$. 令 $CX=(X\times I) / (X\times \set{1})$ 是粘合空间，在这个空间中将子空间 $X\times \set{1}$ 粘合成一点，我们将 $CX$ 称作一个锥 (Cone).
Suspension

令 $X$ 是一个拓扑空间，$I=[0,1]$. $SX$ 是将 $X\times I$ 中 $X\times \set{0}$ 与 $X\times \set{1}$ 分别粘合后形成的粘合空间。这被称之为 Suspension.
Wedge Sum

令 $X$ 和 $Y$ 是两个拓扑空间。令 $x_0\in X,y_0\in Y$，在 $X\sqcup Y$ 中进行粘合，将 $x_0$ 与 $y_0$ 粘合成一个单点，所得到的空间称之为 $X$ 与 $Y$ 的 Wedge Sum，记作 $X\vee Y$.
Attaching Maps

令 $A\subset Y$ 是一个子空间，$f:A\to X$ 是一个连续映射。我们如此构造一个粘合空间：考虑粘合空间，在 $X\sqcup Y$ 中进行粘合，粘合的方式为将 $a$ 与 $f(a)$ 粘合起来，$\forall a\in A$.

这样得出的空间记作 $X\cup_{f} Y$，将 $f$ 称作 Attaching Map.
映射锥 (Mapping Cones)

令 $f:X\to Y$ 是一个映射，映射锥 (Mapping Cone) 即为 $C_f=Y\cup_f CX$. 具体来说，我们将 $X\times \set{0}\subseteq (X\times I) / (X\times \set{1})=CX$ 看作一个子空间并用 $f$ 将其映射至 $Y$. 接着应用 Attaching Map 将两个空间粘合在一起。

拓扑群 (Topological Group)

回忆：群

令 $G$ 是一个群，则我们可以给出两个结构映射：乘法：$m:G\times G\to G$（有时记为 $(g_1,g_2)\to g_1\cdot g_2$）；取逆：$i:G\to G$（记作 $g^{-1}$）.

该两种运算满足一些性质。
定义：拓扑群 (Topological Group)

定义：一个拓扑群 $G$ 既是一个 Hausdorff 的拓扑空间，也是一个群结构，使得两个结构映射 $m$ 与 $i$ 均为连续映射，则我们称其为一个拓扑群 (Topological Group)
拓扑群的基本概念
- 拓扑群的同构 (Isomorphism)
  
  令 $G_1,G_2$ 是两个拓扑群，一个映射 $f:G_1\to G_2$ 被称为是一个同构 (Isomorphism)若 $f$ 是一个同胚且 $f$ 是群之间的同构。
- 子群 (Subgroup)
  
  令 $G$ 是一个拓扑群，考虑 $H\subseteq G$ 是一个子群，我们将 $H$ 装备上 $G$ 的子空间拓扑后，$H$ 也是一个拓扑群，称为 $G$ 的一个子群 (Subgroup).
常见的拓扑群

向量空间 $(\mathbb{R}^n,+)$ 在欧氏拓扑下构成一个拓扑群。

考虑 $S^1=\set{e^{2\pi i\theta}\mid 0\leq \theta<1}$，则 $S^1$ 在乘法下形成一个拓扑群。

令 $T$ 是环面，则若将环面理解为 $T=S^1\times S^1$，则 $T$ 也是拓扑群。

$GL(n,\mathbb{R})$ (可逆矩阵群)、$SL(n,\mathbb{R})$ (行列式为 $1$ 矩阵群)、$O(n)$ (正交矩阵群)、 $SO(n)$ (行列式为 1 的正交矩阵群) 都构成拓扑群（这将在之后展开研究）。
拓扑群的对称性：左平移映射与右平移映射

令 $G$ 是一个拓扑群，选取任意 $x\in G$，定义映射 $L_x:G\to G$ 为 $L_x(g)=x\cdot g$. 我们将这个映射称为左平移映射。

我们容易发现 $L_x$ 是一个双射，且 $L_x$ 需要是一个连续映射（这是连续映射的复合：$G\to G\times G\xrightarrow{m} G:g\to (x,g)\to x\cdot g$）。

并且我们会发现 $L_{x^{-1}}$ 也是连续的并且 $L_x^{-1}=L_{x^{-1}}$，因此 $L_x$ 是一个同胚。（事实上，$L_{x_1x_2}=L_{x_1}\circ L_{x_2}$，$L_e=id_G$）

这告诉我们拓扑群具有高度对称性，我们可以通过同胚映射将任意一个点映射到任意另一个点。

我们也可以定义出右平移映射：$R_x:G\to G,$ $R_x(g)=g\cdot x$. 类似地也有右平移也是一个同胚映射，且有 $R_{x_1x_2}=R_{x_2}\circ R_{x_1}$，$R_e=id_G$.
拓扑群中包含单位元的连通分支是正规子群

令 $G$ 是一个拓扑群，令 $K$ 是 $G$ 中一个连通分支，使得恒等元 $e\in K$。则 $K$ 是 $G$ 中一个闭的正规子群。

回忆：正规子群的定义：若 $H\leq G$，有 $\forall g\in G$, $gH=Hg$，则称 $H$ 是 $G$ 的一个正规子群，记作 $H\vartriangleleft G$.

正规子群的判别：$\forall g\in G,g^{-1}Hg\subset H\Rightarrow H\vartriangleleft G$.

证明：

因为 $K$ 是连通分支，因此 $K$ 是闭集。

$\forall x\in K$，考察 $Kx^{-1}=R_{x^{-1}}(K)$，这是一个连通集合，并且该集合一定会包含恒等元 $e$（这是因为 $x\in K$）. 因此 $Kx^{-1}\subseteq K$ （由于 $K$ 的极大性）.因此 $K$ 确实是 $G$ 的子群。

来验证正规性：$\forall g\in G$，考察 $gKg^{-1}$，这即是 $R_{g^{-1}}\circ L_{g}(K)$. 不难发现这个集合连通且包含了单元元 $e$，因此 $gKg^{-1}\subseteq K$，因此 $K$ 是 $G$ 的正规子群。
连通拓扑群中包含单位元的邻域形成生成元

考虑一个连通的拓扑群 $G$ 与任意一个恒等元 $e$ 的邻域，则该邻域包含的元素形成了一组 $G$ 的生成元。

证明：

令 $e\in U\subseteq G$，其中 $U$ 为开。令 $K=<U>$.

$\forall g\in K$，$gU=L_g(U)\subseteq K$. 由于 $L_g$ 是一个同胚，有 $L_g(U)$ 是一个 $g$ 的邻域。因此 $K$ 是一个开集。

考察 $\forall g\in G\setminus K$，考虑 $gU$，假设 $gU\cap K\neq \varnothing$，则令 $h\in gU\cap K$，$\exists g'\in U$，有 $gg'=h$. 于是 $g=hg'^{-1}\in K$，矛盾。

因而 $gU$ 是 $g$ 的邻域且 $gU\subseteq G\setminus K$，因此 $G\setminus K$ 是开集。

由于 $K$ 是非空集合，$K$ 与 $G\setminus K$ 均为开集，$G$ 为连通而 $G=K\sqcup (G\setminus K)$，有 $G\setminus K=\varnothing$. 因此 $K=G=<U>$.

矩阵群 (Matrix Groups)

常见的矩阵集合
- $Mat_{n\times n}(\mathbb{R})$ 性质研究
  
  $Mat_{n\times n}(\mathbb{R})=\set{n\times n \text{实矩阵}}\cong \mathbb{R}^{n^2}$，其在加法下构成群而在乘法下不是群。
- $GL(n,\mathbb{R})$ （一般线性群）性质的研究
  
  $GL(n,\mathbb{R})=\set{M\in Mat_{n\times n}(\mathbb{R})\mid \det M\neq 0}\subseteq \mathbb{R}^{n^2}$，且是一个开集。
  
  我们来研究一下它的性质。
  
  首先看乘法：
  
  $Mat_{n\times n}(\mathbb{R})\times Mat_{n\times n}(\mathbb{R})\xrightarrow{m} Mat_{n\times n}(\mathbb{R})$ 定义为矩阵乘法，则 $m$ 是连续映射。
  
  因此我们将该乘法限制在开子集 $GL(n,\mathbb{R})$ 上所得到的限制映射也是连续映射。
  
  接着看取逆：
  
  $GL(n,\mathbb{R})\xrightarrow{i} GL(n,\mathbb{R})$ 是取逆映射，由于 $M^{-1}=\cfrac{M^{\star}}{\det M}$，其中 $M^\star$ 是伴随矩阵，伴随是一个连续映射；行列式也是一个连续映射，因此 $i$ 也是一个连续映射。
  
  综上，一般线性群 $GL(n,\mathbb{R})$ 确实是一个拓扑群。
  
  在我们得到一个拓扑群之后，我们通常会研究如下问题：
  - 该拓扑群是否是紧的？答案是否定的，因为 $GL(n,\mathbb{R})$ 是一个欧氏空间的子集，它既不是闭集也不是有界的，故自然不是紧集。
  - 该拓扑群是否是连通的？答案也是否定的，行列式的正负显然至少将 $GL(n,\mathbb{R})$ 切分为了两部分，因此不是连通集合。（$\det:Mat_{n\times n}(\mathbb{R})\to \mathbb{R}$ 是一个连续映射，但 $\det(GL(n,\mathbb{R}))=\mathbb{R}\setminus \set{0}$，该集合不连通，因此 $GL(n,\mathbb{R})$ 也不是连通）
  - 该拓扑群的连通分支是什么？事实上，令 $A=\set{M\in GL(n,\mathbb{R})\mid \det A>0},B=\set{M\in GL(n,\mathbb{R})\mid \det B<0}$，则有 $A,B$ 就是 $GL(n,\mathbb{R})$ 的连通分支。
    
    证明留作练习。提示：由于 $A,B$ 都是欧氏空间中开子集，我们不妨证明 $A,B$ 是道路连通。
    
    我们对矩阵做 $LU$ 分解，其中 $L$ 是下三角阵，$U$ 是上三角阵，我们对 $L$ 与 $U$ 分别移动为对角矩阵，就可以构造一条任意矩阵到对角阵的道路。
    
    对于对角阵，不失一般性地，我们可以通过 $\begin{pmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{pmatrix}$ 构造一个 $\text{diag}(1,1)\to\text{diag}(-1,-1)$ 的连续变换。
- $SL(n,\mathbb{R})$ 性质研究
  
  特殊线性群 $SL(n,\mathbb{R})=\set{M\in GL(n,\mathbb{R})\mid \det M=1}$. 这是一个 $GL(n,\mathbb{R})$ 的子群，故也是一个拓扑群。
  
  上面我们已经说明了它自然是一个拓扑群。
  - 该拓扑群是否是紧的？答案是否定的，尽管它是闭集，但它不是一个有界集合。
  - 该拓扑群是否是连通的？答案是肯定的，它确实是一个连通空间。证明方法：考虑映射 $f:A=\set{M\in GL(n,\mathbb{R})\mid \det M>0}\to SL(n,\mathbb{R})$，$f(M)=\cfrac{M}{(\det M)^{1/n}}$，于是 $f$ 是连续的，由于 $A$ 是连通的，因此 $f(A)=SL(n,\mathbb{R})$ 是连通的。
- 正交矩阵群性质研究
  
  正交矩阵群 $O(n)=\set{M\in GL(n,\mathbb{R})\mid M^TM=I}$，特殊正交矩阵群 $SO(n)=\set{M\in O(n)\mid \det M=1}$. 它们自然也是拓扑群（分别为 $GL(n,\mathbb{R})$ 与 $SL(n,\mathbb{R})$ 的子群）。
  - 正交矩阵群 $O(n)$ 与特殊正交矩阵群 $SO(n)$ 是紧的
    
    正交矩阵群 $O(n)$ 与特殊正交矩阵群 $SO(n)$ 是紧的。
    
    证明：令 $A=(a_{ij})\in O(n)$，则 $A^T A=I$.
    
    于是 $\sum_{j=1}^n a_{ij}a_{kj}=\begin{cases}1&i=k\\0&i\neq k\end{cases}$，令 $f_{ik}:Mat_{n\times n}(\mathbb{R})\to \mathbb{R}$，其中 $f_{ik}(A)=\sum_{j=1}^n a_{ij}a_{jk}$，则 $f$ 是连续映射，且 $f_{ik}^{-1}(0)$ 与 $f^{-1}_{ik}(1)$ 是闭集，因此 $O(n)=\bigcap_{i,k=1,i\neq k}^{n} f_{ik}^{-1}(0) \cap \bigcap_{i=1}^n f_{ii}^{-1}(1)$ 为闭集。
    
    由于$\sum_{j=1}^n |a_{ij}|^2=1,\forall i$，因此 $|a_{ij}|\leq 1$，因此 $O(n)$ 有界。
    
    因此 $O(n)$ 是紧集，类似地有 $SO(n)=O(n)\cap \det^{-1}(1)$ 是紧集。

10. 群作用与商空间

群作用与商空间

抽象代数中的群作用与商空间

群作用

设 $G$ 是一个群，$X$ 是一个集合，我们定义 $G$-作用（记作 $G\curvearrowright X$）：$G\times X\to X$，$(g,x)\to g\cdot x$.

这个作用需要满足 $(hg)\cdot x=h\cdot (g\cdot x)$，且 $e\cdot x=x,\forall x\in G,\forall g,h\in G$.

商群

$X/G=\set{\text{所有 }G\text{ 轨道}}$，轨道的定义为 $x,y\in X$，称 $x,y$ 落在同一轨道上若 $\exists g\in G$ 使得 $x=gy$.
拓扑群的群作用 (Group Action)

令 $G$ 是一个拓扑群，令 $X$ 是一个拓扑空间。一个 $G$-作用是一个映射 $G\times X\xrightarrow{f} X,(g,x)\to g\cdot x$.

该映射 $f$ 需要满足下述性质：
- $f$ 需要是一个连续映射；
- $(hg)\cdot x=h(g\cdot x)$，$\forall x\in X,\forall g,h\in G$
- $e\cdot x=x$，$\forall x\in X$.
拓扑群的商空间 (Quotient Space)

$\forall x,y\in X$，定义一个等价关系：$x\sim y$ 若 $\exists g\in G$ 使得 $x=gy$.

我们首先验证等价关系：

自反性：$x=e\cdot x$；

对称性：$x\sim y$，于是 $\exists g\in G$，使得 $x=gy$，一定有 $y=g^{-1}x$，因此 $y\sim x$；

传递性：$x\sim y,y\sim z$，则 $\exists gh\in G$，使得 $x=gy,y=hz$，于是 $x=g(hz)=(gh)z$，因此 $x\sim z$.

因此这确实是一个等价关系

如此有 $\sim$ 给出了 $X$ 的一个划分 (Partition)，我们将划分中的每一个子集称之为 $G$-轨道 ($G$-orbit).

令 $X/G$ 是对应于 $\sim$ 给出分划的粘合空间，我们将 $X/G$ 称作是商空间 (Quotient Space)，有时我们也称其为轨道空间 (Orbit Space).
商空间的例子
- 环面 Torus
  
  回忆：曾经我们通过矩形对边粘合构成了环面。
  
  现在我们来看如何用商空间观点构造环面。我们固定 $v_1,v_2\in \mathbb{R}^2$，使得 $v_1\not\parallel v_2$.
  
  令 $\Lambda=\mathbb{Z}\cdot v_1 \oplus \mathbb{Z}\cdot v_2\cong \mathbb{Z}^2$，$\Lambda\subseteq \mathbb{R}^2$，这被称作一个格点 (Lattice).
  
  如图是一个 Lattice 的例子，其中 $v_1$ 位于 $x$ 轴。
  
  我们在 $\mathbb{R}^2$ 上定义一个 $\Lambda$-作用，作用的方式为：$(mv_1,nv_2)\cdot(x,y)=(x,y)+mv_1+nv_2$. 这有时也被称为平移作用。
  
  我们考虑商空间 $\mathbb{R^2}/\Lambda$，则该商空间同胚于一个环面。
  
  注意如图中平行四边形，其对边按照相同方向粘合到了一起。
  - *Additional Topic: 黎曼曲面 (Riemann Surface)
    
    我们将 $\Lambda$ 看作 $\mathbb{C}$ 中的一个子集，$\Lambda=\mathbb{Z}\cdot 1\oplus \mathbb{Z}\cdot \tau$，$\tau\in H=\set{z\in \mathbb{C}\mid \text{Im} z>0}$.
    
    那么 $\mathbb{C}/\Lambda$ 还有一个从 $\mathbb{C}$ 诱导的复结构，这个曲面被称作是一个黎曼曲面 (Riemann Surface)。
    
    此外，该曲面亏格 (Genus)是 $1$，这还是一个椭圆曲线。（回忆：复分析讲到的 $\wp$ 函数）
    
    $\text{d}z$ 在 $\mathbb{C}/\Lambda$ 上是一个全纯微分，有 $\int_A \text{d}z=1,\int_B \text{d}z=\tau$.
    
    这意味着，对于不同的 $\tau$，我们可以得到不同的复结构，这与先前环面的拓扑结构于 $\tau$ 无关不同。
    
    事实上，令 $SL(2,\mathbb{Z})\curvearrowright H$，我们定义 $\begin{pmatrix}a&b\\c&d\end{pmatrix} \tau=\cfrac{a\tau+b}{c\tau+d}$，这被称作莫比乌斯变换。那么 $H/SL(2,\mathbb{Z})$ 给出了环面上所有复结构可能的参数空间（模空间 Modulus Space），$\tau\in H/SL(2,\mathbb{Z})$ 一一对应于环面上所有的复结构。
    
    这个参数空间长成什么样呢？
- 射影空间 (Projective Space)
  
  令 $S^n\subseteq \mathbb{R}^{n+1}$ 是单位球面，考虑二元群 $\mathbb{Z}/2\mathbb{Z}=\set{-1,1}$，其中 $-1$ 是生成元，$1$ 是恒等元，群运算定义为恒等运算。定义二元群作用在 $S^n$ 上，其中 $(-1)\cdot x:=-x$.
  
  则 $S^n/(\mathbb{Z}/2\mathbb{Z})=\mathbb{R}P^n$ 得到了实射影空间。
  
  考虑另一种构造：
  
  令 $\mathbb{R}^\star=\mathbb{R}\setminus \set{0}$，我们有 $\mathbb{R}^\star$ 在乘法下成群。我们定义一个群作用 $\mathbb{R}^\star\curvearrowright \mathbb{R}^{n+1}\setminus \set{0}$：$\lambda \cdot(x_1,\cdots,x_{n+1}):=(\lambda x_1,\cdots,\lambda x_{n+1})$，其中 $(x_1,\cdots,x_{n+1})\in \mathbb{R}^{n+1}\setminus \set{0}$.
  
  则 $(\mathbb{R}^{n+1}\setminus \set{0})/\mathbb{R}^{\star}=\mathbb{R}P^n$ 就是实射影空间。
  
  这引出了射影空间上齐次坐标 (Homogeneous Coordinate)的概念：$\mathbb{R}P^n=\set{[x_1:\cdots:x_{n+1}]\mid (x_1,\cdots,x_{n+1})\in \mathbb{R}^{n+1}\setminus\set{0}}$
  
  其中 $[x_1:\cdots:x_{n+1}]=[\lambda x_1:\cdots :\lambda x_{n+1}],\forall \lambda\neq 0$.
  
  在有了齐次坐标之后，我们还能引入如下概念：
  - 典范图册 Canonical Chart
    
    $\mathbb{R}P^n$ 中存在有 $n+1$ 个元素的典范图册 (Canonical Charts)，令 $U_i\subseteq \mathbb{R}P^n$，其中 $U_i=\set{[x_1:\cdots:x_{n+1}]\in \mathbb{R}P^n \mid x_i\neq 0}\subseteq^{\text{open}} \mathbb{R}P^n$，则我们可以将这中坐标写成 $[x_1,\cdots,x_i,\cdots,x_{n+1}]=[\cfrac{x_1}{x_i}:\cdots:1:\cdots:\cfrac{x_{n+1}}{x_i}]$.
    
    此时有 $U_i$ 同胚于 $\mathbb{R}^n$，这是由于在固定 $x_i$ 为 $1$ 后，其余元素已经没有所谓的“自由度”了。与此同时，$\set{U_i}_{i=1}^{n+1}$ 是一个射影空间 $\mathbb{R}P^n$ 的开覆盖。（因此，$\mathbb{R}P^n$ 是一个流形）
  对于复射影空间，$\mathbb{C}^\star:=\mathbb{C}\setminus\set{0}$，我们定义群作用 $\mathbb{C}^\star \curvearrowright \mathbb{C}^{n+1}\setminus\set{0}:\lambda(x_1,\cdots,x_{n+1})=(\lambda x_1,\cdots,\lambda x_{n+1})$.
  
  在这个群作用下我们得到了复射影空间 $\mathbb{C}P^n$，也能定义齐次坐标和典范图册：$U_i=\set{[x_1:\cdots:x_{n+1}]\in\mathbb{C}P^n\mid x_i\neq 0}\subseteq^{\text{open}} \mathbb{C}P^n$.
  
  也有 $U_i$ 同胚于 $\mathbb{C}^n$，且 $U_i$ 形成了 $\mathbb{C}P^n$ 的开覆盖。（因此，$\mathbb{C}P^n$ 是一个复流形）
  - *Additional Topic: $\mathbb{C}P^n$ 上的 Zariski Topology
    
    定义 $\mathbb{C}P^n$ 上的另一种拓扑，称作 Zariski Topology。
    
    一个多项式 $f(x_1,\cdots,x_{n+1})$ 被称作是一个齐次多项式 (Homogeneous)，如果 $f(\lambda x_1,\cdots,\lambda x_{n+1})=\lambda^d f(x_1,\cdots,x_{n+1})$，其中 $d\in \mathbb{Z}_{\geq 0}$，被称为是齐次多项式的次数 (Degree)。
    
    我们如此定义 Zariski Topology：一个子集 $F\subset \mathbb{C}P^n$ 是闭集，若 $F$ 是某一些 $\mathbb{C}[x_1,\cdots,x_{n+1}]$ 中齐次多项式的公共零点。这被称为是射影空间的 Zariski Topology.
    
    小练习：事实上，我们定义 $U_i=\set{[x_1:\cdots:x_{n+1}]\in \mathbb{C}P^n\mid x_i\neq 0}\subset \mathbb{C}P^n$，我们在 $\mathbb{C}P^n$ 上装备 Zariski Topology，考虑 $U_i$ 上的子空间拓扑，则有 $U_i$ 同胚于装备了 Zariski Topology 的 $\mathbb{C}^n$。
    
    提示：$\set{[x_1,\cdots,x_{n+1}]\in \mathbb{C}P^n\mid f(x_1,\cdots,x_{n+1})=0}\cap U_{n+1}$，$f$ 齐次可以被写成 $\set{(x_1,\cdots,x_n)\in \mathbb{C}^n\mid g(x_1,\cdots,x_n)=f(x_1,\cdots,x_n,1)=0}$.
- 子群作用
  
  令 $G$ 是一个拓扑群，$H$ 是 $G$ 的子群。那么存在作用 $H\curvearrowright G$：$h\cdot g=h\cdot g$（其中右边是群 $G$ 中乘法，左边是作用的符号），$h\in H,g\in G$.
  
  可以验证 $G/H$ 是所有右陪集组成的集合 $=\set{Hg\mid g\in G}$。
- 矩阵群的作用
  
  考虑矩阵群 $O(n)$（正交矩阵群）的作用，$O(n)\curvearrowright S^{n-1}\subseteq \mathbb{R}^n$. 这个群作用是传递的 (Transitive)（回忆：传递指的是 $\forall x\in S^{n-1}$，这个点所在的轨道是全空间），或者说 $\forall x,y\in S^{n-1}$，$x,y$ 在同一个 $O(n)$-轨道中，也就是 $\exists A\in O(n)$，使得 $Ax=y$.
  
  证明：
  
  $\forall x_1\in S^{n-1}$，将其延拓为一组 $\mathbb{R}^n$ 的标准正交基 $x_1,\cdots, x_{n}$.
  
  类似地 $\forall y_1\in S^{n-1}$，也可以将其延拓为一组 $\mathbb{R}^n$ 的标准正交基 $y_1,\cdots,y_n$.
  
  那么存在正交矩阵 $A\in O(n)$，使得 $(Ax_1,\cdots,Ax_n)=(y_1,\cdots,y_n)$.
  
  于是 $Ax_1=y_1$.
  
  考虑一个嵌入映射：$O(n-1)\to O(n)$：$B\to\begin{pmatrix}1&0\\0&B\end{pmatrix}$，并且在这个嵌入下，$O(n-1)$ 可以看作是 $O(n)$ 的一个子群。
  
  现在令 $e_1=\begin{pmatrix}1\\0\\\vdots\\0\end{pmatrix},\cdots,e_n=\begin{pmatrix}0\\0\\\vdots\\1\end{pmatrix}$ 是一组 $\mathbb{R}^n$ 的标准基，
  
  我们有 $Ae_1=e_1$ $\Leftrightarrow$ $A=\begin{pmatrix}1&0\\0&B\end{pmatrix},B\in O(n-1)$.
  
  于是我们把 $O(n-1)\subseteq O(n)$ 称作 $e_1$ 的稳定化子 (Stabilizer)。
  
  我们令 $\pi:O(n)\to S^{n-1}:A\to Ae_1$，我们有 $\pi$ 是连续的且是满射（因为 $O(n)\curvearrowright S^{n-1}$ 是传递的）。
  
  由于 $O(n)$ 是紧的，$S^{n-1}$ 是 Hausdorff，因此 $\pi$ 是粘合映射。
  
  我们考虑这个粘合映射对应的分划：这个分划即为所有的左陪集 $\set{AO(n-1)\mid A\in O(n)}$.
  
  因此如果我们取商群 $O(n)/O(n-1)$，这个群同胚于 $S^{n-1}$.
  
  类似地，可以考虑嵌入 $SO(n-1)\to SO(n)$，我们可以得到 $SO(n)/SO(n-1)$ 同胚于 $S^{n-1}$.
构造商空间的粘合映射一定是开映射

令 $G$ 作用于 $X$ 上，若考虑粘合映射 $\pi:X\to X/G$，则该粘合映射一定是开映射，也就是说，$\forall$ 开集 $U\subseteq X$，有 $\pi(U)$ 是 $X/G$ 中开集。

证明：取开集 $U$， $\pi(U)\subseteq X/G$，它是开集当且仅当 $\pi^{-1}(\pi(U))$ 是开集。

我们考虑证明如下事实：$\pi^{-1}(\pi(U))$ 总可以写成 $\bigcup_{g\in G}g\cdot U$.

$\forall x\in \bigcup_{g\in G}g\cdot U$，$\exists g\in G,y\in U$，使得 $x=gy$，于是 $\pi(x)=\pi(y)\in \pi(U)$；

令 $x\in \pi^{-1}\pi(U)$，$\pi(x)\in \pi(U)$，也就是 $\exists y\in U$，使得 $\pi(x)=\pi(y)$，也就是 $\exists g\in G$，使得 $x=gy$.

因此事实得到证明。由于 $U$ 是开集，由于平移映射 $g:X\to X,x\to g\cdot x$ 是一个同胚，有 $gU$ 是一个开集，因此 $\pi^{-1}(\pi(U))=\bigcup_{g\in G}gU$ 是开集。

因此这是一个开映射。

11. 同伦

群作用收尾

回顾：商空间粘合映射

考虑 $G\curvearrowright X$ 给出粘合映射，有 $\pi:X\to X/G$，我们有 $\pi$ 是一个开映射。
整体空间与商空间连通性的关系

考虑群作用 $G\curvearrowright X$，$X/G$ 与群 $G$ 都是连通的，则 $X$ 是连通的。

证明：根据连通性的定义，假设 $X=A\cup B$，使得 $A\cap B=\varnothing$，且 $A,B$ 为非空开集。

我们知道，$\pi:X\to X/G$ 是开映射，因此 $X/G=\pi(A)\cup \pi(B)$，并且 $\pi(A), \pi(B)$ 都是非空开集。因此 $\pi(A)\cap \pi(B)\neq \varnothing$ （$X/G$ 是连通），令 $\pi(x)\in \pi(A)\cap \pi(B)$，则有 $A\cap Gx\neq\varnothing, B\cap Gx\neq \varnothing$. 不仅如此，我们有 $Gx=(A\cap Gx)\sqcup (B\cap Gx)$.

然而，令 $f:G\to X, f(g)=gx$，$f$ 是一个连续映射因为 $f$ 是 $G\to G\times X\to X$ 的复合，两个映射分别是嵌入映射与群作用的结构映射，故 $Gx=f(G)$ 也是连通集合，这与上面 $Gx$ 的定义矛盾。
特殊正交群 $SO(n)$ 是连通的

特殊正交群 $SO(n)$ 是连通的。

证明：归纳法。$SO(1)$ 只有一个单点，故是连通集。

上节课我们讲到 $SO(n+1)/SO(n)\cong S^{n}$，由于 $S^n$ 是连通的，根据归纳假设有 $SO(n)$ 是连通的，根据上面的定理有 $SO(n+1)$ 是连通的。

同伦理论 (Homotopy Theorem)

引入动机
- 为了引入同伦群 (Homotopy Groups)
  
  定义拓扑不变量：同伦群 (Homotopy Groups)，这门课将只会讲授一维同伦群（基本群, Fundamental Group）。
- 引入同伦等价 (Homotopy Equivalences)
  
  为了引入一个比同胚稍弱的等价关系，将复杂的空间等价为简单的空间。
同伦 (Homotopy)

让我们先来看几个例子：

如图，圆周打到球面上能“缩”成一点。

如图，圆周打到环面上有时能“缩”成一点（绿圈），有时不能（橙圈）。这意味着环面与球面在一定意义下是不同的。

又如：考虑如下情形：

球面在 $\mathbb{R}^3$ 中能收缩为一点，但不能在 $S^2$ 中缩成一点。

同理，$S^n$ 在 $\mathbb{R}^{n+1}$ 可以缩成一点，但不能在 $S^n$ 中缩成一点。

我们应该怎样表示映射的“收缩”呢？来看下面的定义。
- 同伦的定义 (Homotopic)
  
  令 $f,g$ 为 $X\to Y$ 连续映射，则 $f$ 与 $g$ 同伦 (Homotopic) 若 $\exists$ 连续映射 $F:X\times I\to Y$，其中 $I=[0,1]$，使得 $F(x,0)=f(x),F(x,1)=g(x),\forall x\in X$.
  
  记作 $f\underset{F}{\simeq}g$
  
  从直观上看，这即是
- 相对同伦的定义 (Relative Homotopic)
  
  若 $\exists A\subset X$ 使得 $f|_A=g|_A$，若 $\exists F:X\times I\to Y$ 使得 $F(x,0)=f(x); F(x,1)=g(x),\forall x\in X$，且 $F(x,t)=f(x),\forall x\in A,t\in [0,1]$，称 $f$ 与 $g$ 相对于子空间 $A$ 同伦. 记作 $f\underset{F}{\simeq}g\text{ rel } A$.
  
  直观上看，这意味着 $A$ 里面的点在同伦时始终保持不动。
- 例子：直线同伦 (Straight-Line Homotopy)
  
  令 $C\subset \mathbb{R}^n$ 是一个凸集（Convex Set，即为 $\forall x,y\in C$，有 $\forall t\in [0,1]$，$tx+(1-t)y\in C$），令 $f,g:X\to C$ 是任意两个连续映射，则有 $f\simeq g$.
  
  证明：令 $F(x,t)=(1-t)f(x)+tg(x)$，则有 $f\underset{F}{\simeq} g$.
- 同伦是一个等价关系
  
  引理：对所有 $X\to Y$ 的连续映射，同伦是一个等价关系。
  
  证明：自反性 $f\simeq f$：$F(x,t)=f(x),\forall x\in X,t\in I$ 即得；
  
  对称性 $f\underset{F}{\simeq} g\Rightarrow g\simeq f$：令 $G(x,t)=F(x,1-t),\forall x\in X,t\in I$，则有 $G$ 是连续的且 $G(x,0)=g(x), G(x,1)=f(x)$，于是 $g\underset{G}{\simeq} f$.
  
  传递性：$f\underset{F}{\simeq} g,g\underset{G}{\simeq} h\Rightarrow f\simeq h$：定义 $H(x,t)=\begin{cases}F(x,2t)&0\leq t\leq \frac{1}{2}\\G(x,2t-1)&\frac{1}{2}\leq t\leq 1\end{cases}$
  
  于是有 $f\underset{H}{\simeq} h$.
  
  注：相对同伦也是一个等价关系。这里略去不再证明。
- 复合映射间的同伦（同伦被复合保持）
  
  如图所示，若 $f\underset{F}{\simeq} g\text{ rel } A$，则 $h\circ f\underset{h\circ F}{\simeq} h\circ g\text{ rel } A$.
  
  如图所示，若 $g\underset{G}{\simeq} h\text{ rel } B$，则 $g\circ f\underset{G(f(x),t)}{\simeq} h\circ f\text{ rel } f^{-1}(B)$.
  
  证明：
  
  先看上面的式子。$F:X\times I\to Y$，有 $F(x,0)=f(x),F(x,1)=g(x),\forall x\in A$，并且 $F(x,t)=f(x),\forall x\in A,t\in I$. 于是 $h\circ F(x,0)=h\circ f(x), h\circ F(x,1)=h\circ g(x)$.
  
  不仅如此，$h\circ F(x,t)=h\circ f(x),\forall x\in A,t\in I$，由于 $h\circ F$ 确实连续，于是 $h\circ f\underset{h\circ f}{\simeq} h\circ g\text{ rel } A$.
  
  再看下面的式子。有 $G(y,0)=g(y), G(y,1)=h(y),\forall y\in Y$. 且 $G(y,t)=g(y),\forall y\in B$ 于是 $G(f(x),0) = g(f(x)), G(f(x),1)=h(f(x))$. 另外 $G(f(x),t)=g(f(x)),\forall x\in f^{-1}(B)$. 类似地即有 $g\circ f\underset{G(f(x),t)}{\simeq} h\circ f\text{ rel } f^{-1}(B)$.
基本群 (Fundamental Group)

考虑道路 $\gamma:[0,1]\to X$ 使得 $\gamma(0)=\gamma(1)$ （注：这种情况等价于给出 $S^1\to X$），我们将这样的道路称作是 $X$ 中环路 (Loop)。

我们在 $X$ 中选择一个标志点 (Base Point) $p\in X$，考虑集合：$X$ 中所有环路，使得 $\gamma(0)=\gamma(1)=p$ 或者说这些环路的基础点为 $p$。令 $A=\set{0,1}\subseteq[0,1]$，则相对 $A$ 同伦的关系是一个等价关系，我们记一个环路 $\gamma$ 所在的等价类为 $<\gamma>$.

我们来定义乘法：令 $\alpha,\beta$ 为两个基础点为 $p$ 的环路，令 $\alpha\cdot \beta:[0,1]\to X$，形如下图所示：

我们定义乘积为 $\alpha\cdot\beta(t)=\begin{cases}\alpha(2t)&0\leq t<\cfrac{1}{2}\\\beta(2t-1)&\cfrac{1}{2}\leq t\leq 1\end{cases}$.

问题：这个乘法是否满足严格的结合律？

然而并不是。$(\alpha\cdot \beta)\cdot\gamma(t)=\begin{cases}\alpha(4t)&0\leq t<1/4\\\beta(4t-1)&1/4\leq t<1/2\\\gamma(2t-1)&1/2\leq t\leq 1\end{cases}$

但 $\alpha\cdot(\beta\cdot\gamma)(t)=\begin{cases}\alpha(2t)&0\leq t<1/2\\\beta(4t-2)&1/2\leq t<3/4\\\gamma(4t-3)&3/4\leq t\leq 1\end{cases}$

这两个映射“环绕的速度”是不相同的。

为了改进这一点，我们不再考虑道路自己，而是考虑道路的同伦类，即 $<a>\cdot <\beta>:=<a\cdot \beta>$ 上的运算。

如此，我们需要解决如下几个问题：
1. 验证定义是良定的；
事实上，定义确实是良定的：令 $\alpha'\underset{F}{\simeq} \alpha\text{ rel }\set{0,1}, \beta'\underset{G}{\simeq} \beta\text{ rel }\set{0,1}$，则令 $H(s,t)=\begin{cases}F(2s,t)&0\leq s\leq 1/2\\G(2s-1,t)&1/2\leq s\leq 1\end{cases}$

从而 $\alpha'\cdot \beta'\underset{H}{\simeq} \alpha\cdot\beta$.
1. 验证如下定理：
考虑所有基本点为 $p$ 的 $X$ 中环路同伦类组成的集合，这个集合构成了一个群，群的乘法为 $<\alpha>\cdot<\beta>=<\alpha\cdot\beta>$.

证明：

结合律：

即要证明，$(\alpha\cdot\beta)\cdot\gamma\simeq\alpha\cdot(\beta\cdot\gamma) \text{ rel }\set{0,1}$.

考虑 $f:[0,1]\to [0,1]$，有 $f(s)=\begin{cases}2s&0\leq s\leq 1/4\\s+1/4&1/4\leq s\leq 1/2\\\cfrac{s+1}{2}&1/2\leq s\leq 1\end{cases}$

这是对 $[0,1]$ 的重新参数化，且 $(\alpha\cdot\beta)\cdot\gamma = (\alpha\cdot(\beta\cdot\gamma))\circ f$

我们做出如下的声称：$f$ 同伦于 $id: [0,1]\to [0,1]\text{ rel }\set{0,1}$.

令 $F(s,t)=\begin{cases}(2-t)s&0\leq s\leq 1/4\\s+1/4-t/4&1/4\leq s\leq 1/2\\(1/2+t/2)s+1/2-t/2&1/2\leq s\leq 1\end{cases}$，于是 $f\underset{F}{\simeq} id\text{ rel }\set{0,1}$.

于是 $(\alpha\cdot\beta)\cdot\gamma=(\alpha\cdot(\beta\cdot\gamma))\circ f\simeq (\alpha\cdot (\beta\cdot\gamma))\circ id= \alpha\cdot(\beta\cdot \gamma)\text{ rel }\set{0,1}$.

恒等元：

令 $e(t)=p,\forall t\in [0,1]$，则考察 $f$，有 $f(s)=\begin{cases}0&0\leq s\leq 1/2\\2s-1&1/2\leq s\leq 1\end{cases}$

此时有 $e\cdot \alpha=\alpha\circ f$.

同理可以构造出 $f$ 同伦于 $id$.

因此 $e\cdot\alpha=\alpha\circ f\simeq \alpha\circ id=\alpha\text{ rel }\set{0,1}$.

也就是 $<e>\cdot<\alpha>=<\alpha>$.

类似地 $<\alpha>\cdot<e>=<\alpha>$.

逆元：

令 $\alpha^{-1}(s)=\alpha(1-s),0\leq s\leq 1$.

首先验证良定义：若 $\alpha\underset{F}\simeq \beta$，则 $\alpha^{-1}\underset{G}\simeq\beta^{-1}$，其中 $G(s,t)=F(1-s,t)$，因此 $<\alpha>^{-1}$ 不依赖于代表元的选取。

令 $f:I\to I$，有 $f(s)=\begin{cases}2s&0\leq s\leq 1/2\\2-2s&1/2\leq s\leq 1\end{cases}$.

则 $\alpha\cdot\alpha^{-1}=\alpha \circ f$.

可以证明 $f\simeq g\text{ rel }\set{0,1}$，有 $g(s)=0,\forall 0\leq s\leq 1$.

因此 $\alpha\cdot\alpha^{-1}=\alpha\circ f\simeq \alpha\circ g=e\text{ rel }\set{0,1}$.

类似地，$\alpha^{-1}\cdot\alpha\simeq e\text{ rel }\set{0,1}$.

因而 $<\alpha^{-1}>=<\alpha>^{-1}$.

我们将这个群称作 $X$ 关于基点 $p$ 处的基本群 (Fundamental Group)，记作 $\pi_1(X,p)$. $\forall <\gamma(t)>\in \pi_1(X,p)$，它是一些环路的等价类，且 $\gamma(t)$ 都落在包含点 $p$ 的道路连通分支中。

因此，当我们研究基本群时，我们总可以假设 $X$ 是道路连通的。

注：为什么是 $\pi_1$？

实际上我们可以定义一般的同伦群：我们令 $S^n$ 是 $n$ 维球面，我们可以固定 $s_0\in S^n$，考虑所有的同伦类，该同伦是相对于 $s_0$ 的同伦，所有这样的同伦类（$S^n\xrightarrow{\gamma}X,\gamma(s_0)=p$）也可以构成群，记作 $\pi_n$，$n$ 维同伦群。（本课只研究 $n=1$ 情形）

12. 基本群

基本群

回忆：基本群的定义

$\pi_1(X,p)=\set{<\gamma>\mid \gamma\text{ loop at } p}$，其中 $\gamma$ 是一个基础点为 $p$ 的环路。
- 注：基本群定义的推广
  
  对基本群的定义我们有如下的推广：令 $\gamma_1,\gamma_2\in X$ 是两个道路，使得 $\gamma_1(1)=\gamma_2(0)$，我们还可以令 $\gamma_1\cdot \gamma_2(s)=\begin{cases}\gamma_1(2s)&0\leq s\leq 1/2\\\gamma_2(2s-1)&1/2\leq s\leq 1\end{cases}$，这是 $\gamma_1$ 与 $\gamma_2$ 的拼接。
  
  如果我们如此操作则可以得到下述性质：
  - 若 $\gamma_1\simeq \gamma_1'\text{ rel }\set{0,1},\gamma_2\simeq\gamma_2'\text{ rel }\set{0,1}$，则 $\gamma_1\cdot \gamma_2\simeq \gamma_1'\cdot\gamma_2'\text{ rel }\set{0,1}$.
  - 若 $\gamma_1(1)=\gamma_2(0), \gamma_2(1)=\gamma_3(0)$，则 $\gamma_1\cdot(\gamma_2\cdot\gamma_3)\simeq (\gamma_1\cdot\gamma_2)\cdot\gamma_3\text{ rel }\set{0,1}$.
  - 令 $\gamma^{-1}(s)=\gamma(1-s)$，则 $\gamma\cdot\gamma^{-1}\simeq \text{constant path at } \gamma(0)\text{ rel }\set{0,1}$，且 $\gamma^{-1}\cdot\gamma\simeq \text{constant path at }\gamma(1)\text{ rel }\set{0,1}$.
  不难注意到这些性质与我们定义基本群时类似。
问：令 $X$ 是道路连通空间，问 $\pi_1(X,p)$ 是否依赖于 $p$ 的选取？
$\pi_1$ 群的结构与 $p$ 的选取无关

令 $X$ 是道路连通，则任取两个点 $p,q\in X$，$\pi_1(X,p)$ 与 $\pi_1(X,q)$ 是同构的。我们将同构类记作 $\pi_1(X)$.

证明：

选取道路 $\gamma$ 连接 $p$ 与 $q$，定义一个映射 $\gamma_\star:\pi_1(X,p)\to\pi_1(X,q)$, 有 $<\alpha>\to <\gamma^{-1}\cdot\alpha\cdot\gamma>$

由注的第一条，我们有 $\gamma_\star$ 是良定义的；

由注的第二、第三条，有 $\begin{aligned}\gamma_\star(<\alpha>\cdot<\beta>)&=<\gamma^{-1}\cdot \alpha\cdot\beta\cdot\gamma>=<\gamma^{-1}\alpha\gamma \gamma^{-1}\beta\gamma>\\&=<\gamma^{-1}\alpha\gamma><\gamma^{-1}\beta\gamma>=\gamma_\star(\alpha)\cdot\gamma_\star(\beta)\end{aligned}$（式中省略了一些乘号）

因此 $\gamma_\star$ 是一个群同态；

那么 $\gamma_\star$ 是否是群同构呢？由第三条，我们知道 $(\gamma^{-1})_\star$ 是 $\gamma_\star$ 的逆，因此正反映射都是群同态，$\gamma_\star$ 是群同构。
- 连续映射诱导基本群群同态
  
  思考：拓扑空间 $X$对应了一个 $\pi_1$ 群，若 $f:X\to Y$ 连续映射，该映射是否诱导 $\pi_1$ 群之间的同态呢？
  
  事实上，令 $p\in X$，$f(p)=q\in Y$，$\alpha:[0,1]\to X$ 是一个环路，考虑 $f\circ \alpha$，则这得到了 $Y$ 中一个基本点为 $q$ 的环路。
  
  如果 $\alpha\simeq\alpha_1\text{ rel }\set{0,1}$，自然有 $f\circ\alpha\simeq f\circ\alpha_1\text{ rel }\set{0,1}$.
  
  因此我们得到映射，记作 $f_\star:\pi_1(X,p)\to\pi_1(Y,q)$，$<\alpha>\to<f\circ\alpha>$.
  
  我们验证它是群同态：
  
  $f_\star(<\alpha><\beta>)=f_\star(<\alpha\cdot\beta>)=<(f\circ\alpha)(f\circ\beta)>=f_\star(<\alpha>)f_\star(<\beta>)$.
  
  其自然是一个群同态。
连续映射诱导群同态映射的基本性质

令 $f:X\to Y$，$g:Y\to Z$ 是两个连续映射，则 $(g\circ f)_\star=g_\star\circ f_\star$，$(id_X)_\star=id_{\pi_1(X)}$。

证明：

$(g\circ f)_\star(<\alpha>)=<g\circ f\circ\alpha>=g_\star(<f\circ \alpha>)=g_\star\circ f_\star(\alpha)$.

$(id_{X})_\star(<\alpha>)=<id_X\circ\alpha>=<\alpha>$.
同胚映射诱导基本群的同构映射

若 $f:X\to Y$ 是一个同胚映射，则 $f_\star$ 是一个群同构。

证明：考虑 $X\xrightarrow{f} Y\xrightarrow{f^{-1}} X$，$Y\xrightarrow{f^{-1}}X\xrightarrow{f}Y$.

于是 $(f^{-1})_\star\circ f_\star=(f^{-1}\circ f)_\star=(id_X)_\star=id_{\pi_1(X)}$, $f_\star\circ (f^{-1})_\star=(f\circ f^{-1})_\star=(id_Y)_\star=id_{\pi_1(Y)}$.

自然，$f_\star$ 是一个同构。
基本群是拓扑不变量

根据上面的定理，我们可以看出 $\pi_1(X)$ 确实是一个拓扑不变量。（由于同胚映射保持基本群同构）
- 注：基本群定义出的函子 (Functor)
  
  事实上，在先前的构造中，我们构造了一个叫做函子 (Functor) 的结构 $\pi_1$，它给出了一个从所有带有基本点(base point)的拓扑空间到群范畴的对应。
  
  如果给定一个拓扑空间 $X$ 以及一个 base point $p$，我们得到了一个 $\pi_1(X,p)$ 的对应。
  
  若给出 $f:(X,p)\to (Y,q)$，则这被对应到了 $f_\star:\pi_1(X,p)\to \pi_1(Y,q)$.
  
  并且该对应满足 $(g\circ f)_\star=g_\star\circ f_\star$，$(id_X)_\star=id_{\pi_1(X,p)}$.
  
  （回忆：拓扑学范畴研究的是对象与态射）
基本群的例子
- $\mathbb{R}^n$ 中凸集的基本群
  
  设 $C\subset \mathbb{R}^n$，则 $\pi_1(C)=\set{e}$. （任意给一条环路，环路可以通过直线同伦达到恒等映射）
  
  我们也称这种情况为单连通 (simply-connected)，即称拓扑空间 $X$ 为单连通的，若 $X$ 中的基本群为平凡群 $\set{e}$。
- 圆周 $S^1$ 的基本群
  
  令 $S^1=\set{e^{2\pi i\theta}\mid 0\leq \theta<1}$.
  
  若道路不转圈，则其跟恒等道路同伦；
  
  还可以注意到顺时针转 $k$ 圈的道路彼此同伦。
  
  我们猜想：$\pi_1(S^1)=\mathbb{Z}$.
  
  令 $\pi:\mathbb{R}\to S^1$，$x\to e^{2\pi ix}$.
  
  $\forall n\in\mathbb{Z}$，考虑道路：$\gamma_n(s)=ns$，$s\in [0,1]$.
  
  考虑 $\pi\circ\gamma_n$，则它是一个 $S^1$ 上的环路，基本点为 $1\in S^1$。形象地看，这是一个这样的映射：
  
  那么 $\pi\circ\gamma_n$ 就是沿着 $S^1$ 转 $n$ 圈的道路。
  
  我们期望证明下面的定理：令 $\phi:\mathbb{Z}\to \pi_1(S^1,1)$，$\phi(n):=<\pi\circ\gamma_n>$，则 $\phi$ 是一个群同构。
  - 一个基本的观察
    因为 $\mathbb{R}$ 是一个凸集，令 $\gamma:[0,1]\to\mathbb{R}$，使得 $\gamma(0)=0,\gamma(1)=n$，则 $\gamma\simeq \gamma_n\text{ rel }\set{0,1}$，由直线同伦给出。
  我们首先证明下面的引理：
  - $\phi$ 是一个群同态
    
    $\phi$ 是一个群同态。
    
    证明：
    
    我们想要证明 $\phi(m+n)=\phi(m)\cdot \phi(n),\forall m,n\in \mathbb{Z}$.
    
    令 $\sigma:[0,1]\to\mathbb{R}$，$\sigma(s)=\gamma_n(s)+m$. 我们有 $\pi\circ\sigma=\pi\circ\gamma_n$.
    
    并且，$(\gamma_m\cdot\sigma)(0)=0$，$(\gamma_m\cdot\sigma)(1)=m+n$.
    
    因此，$\phi(m+n)=<\pi\circ \gamma_{m+n}>=<\pi\circ(\gamma_m\cdot\sigma)>$，最后一个等号由上面的观察给出。
    
    于是这又可以写成 $<(\pi\circ\gamma_m)\cdot(\pi\circ\sigma)>=<(\pi\circ\gamma_m)\cdot(\pi\circ\gamma_n)>=\phi(m)\cdot\phi(n)$.
    
    因此这是一个群同态。
  - 道路提升引理 (Path-lifting Lemma)
    
    考虑道路 $\sigma:[0,1]\to S^1$，使得 $\sigma(0)=1$。那么 $\exists!\tilde\sigma:[0,1]\to \mathbb{R}$（存在且唯一），使得 $\tilde\sigma(0)=0$ 且 $\pi\circ\tilde\sigma=\sigma$.
    
    此时我们将 $\tilde\sigma$ 称为 $\sigma$ 的一个提升 (Lift)。
    
    直观来看，这就是在说
    
    如图所示的道路对应是唯一的。（这也能从直观上解释为什么引理是正确的）
    
    证明：
    
    令 $U=S^1\setminus\set{-1}$，$V=S^1\setminus\set{1}$.
    
    有 $\set{U,V}$ 是 $S^1$ 的开覆盖，并且 $\pi|_{(n-1/2,n+1/2)}:(n-1/2,n+1/2)\to U$ 同胚；$\pi|_{(n,n+1)}:(n,n+1)\to V$ 同胚（$\forall n\in \mathbb{Z}$）。
    
    由于 $[0,1]$ 是一个紧度量空间，根据 Lebesgue 引理，$\exists 0=t_0<t_1<\cdots<t_n=1$，有 $[t_i,t_{i+1}]\subset \sigma^{-1}(U)$ 或 $\sigma^{-1}(V)$.
    
    （
    
    回忆：
    
    Lebesgue 引理 (Lebesgue's Lemma)
    
    令 $X$ 是一个紧的度量空间，令 $X=\bigcup_\alpha U_\alpha$ 是 $X$ 的开覆盖。则 $\exists \delta>0$，将 $\delta$ 称作关于 $X$ 的开覆盖 $\set{U_\alpha}$ 的 Lebesgue 数 (Lebesgue Number)，使得 $\forall X$ 的子集，若其直径小于 $\delta$，则其一定被包含在某一个 $U_\alpha$ 里。
    
    ）
    
    因为 $\sigma(0)=1\not\in V$，有 $\sigma([0,t_1])\subset U$. 令 $f=(\pi|_{(-1/2,1/2)})^{-1}$，令 $\tilde\sigma(s)=f\circ \sigma(s),0\leq s\leq t_1$，于是 $\pi\circ\tilde\sigma(s)=\sigma(s)$.
    
    假设我们已经在 $[0,t_k]$ 上定义好了 $\tilde\sigma$，我们将其延拓到 $[0,t_{k+1}]$ 上。
    
    若 $\sigma([t_k,t_{k+1}])\subset U$，假设 $\sigma([t_k,t_{k+1}])\subset(n-1/2,n+1/2),n\in \mathbb{Z}$.
    
    那么令 $g:=(\pi|_{(n-1/2,n+1/2)})^{-1}$，令 $\tilde\sigma(s)=g\circ\sigma(s),t_k\leq s\leq t_{k+1}$，于是 $\pi\circ\tilde\sigma=\sigma,0\leq s\leq t_{k+1}$.
    
    若 $\sigma([t_k,t_{k+1}])\subset V$，假设 $\sigma([t_k,t_{k+1}])\subset (n,n+1),n\in \mathbb{Z}$，于是令 $h:=(\pi|_{n,n+1})^{-1}$，令 $\tilde\sigma(s)=h\circ\sigma(s),t_k\leq s\leq t_{k+1}$，于是 $\pi\circ\tilde\sigma=\sigma,0\leq s\leq t_{k+1}$.
    
    由归纳法，我们总可以将 $\sigma$ 提升为 $\tilde\sigma$.
    
    唯一性由每一步提升的唯一性即得。
  - 同伦提升引理 (Homotopy-lifting Lemma)
    
    若考虑同伦 $F:I\times I\to S^1$ 连续映射，使得 $F(0,t)=F(1,t)=1,\forall 0\leq t\leq 1$，即该同伦保持 $\set{0,1}$ 不动。
    
    则 $\exists! \tilde F:I\times I\to \mathbb{R}$，使得 $\pi\circ \tilde F= F$（提升条件），$\tilde F(0,t)=0, \forall 0\leq t\leq 1$（初始条件）。
    
    证明：
    
    证明的思路与道路提升引理类似。
    
    由于 $I\times I$ 也是一个紧的度量空间，由于 Lebesgue 引理，$\exists 0=s_0<s_1<\cdots<s_m=1,0=t_1<t_2<\cdots<t_k=1$，使得 $[s_i,s_{i+1}]\times[t_j,t_{j+1}]\subset F^{-1}(U)$ 或 $F^{-1}(V)$，其中 $U=S^1\setminus\set{-1}$，$V\in S^1\setminus\set{1}$.
    
    由于 $F(\set{0}\times [0,t_1])=1\not\in V$，则令 $f=(\pi|_{(-1/2,1/2)})^{-1}$，令 $\tilde F(s,t)=f\circ F(s,t), \forall s,t\in [0,s_1]\times [0,t_1]$.
    
    之后的证明，可以对两个指标做归纳法，于是 $\exists!\tilde F$ 使得 $\pi\circ\tilde F=F$，且 $\tilde F(0,t)=0,\forall 0\leq t\leq 1$.
  在有了上述两个引理后，我们现在可以证明 $\pi_1(S^1,1)\cong \mathbb{Z}$ 了，即 $\phi:\mathbb{Z}\to \pi_1(S^1,1),\phi(n)=<\pi\circ\gamma_n>$ 是一个群同构。
  
  证明：
  
  根据我们的引理，这是一个群同态。我们只需要证明单、满射。
  
  满射：由道路提升引理，我们可以看出 $\phi$ 是一个满射。
  
  单射：假设 $\phi(n)=e\in \pi_1(S^1,1)$，则由定义 $\exists F:I\times I\to S^1$，使得 $F(s,0)$ 是常数道路，$F(s,1)=\pi\circ\gamma_n(s)$，其中 $F(0,t)=F(1,t)=1\in S^1,\forall t$.
  
  由同伦提升引理，$\exists\tilde F:I\times I\to \mathbb{R}$，由 $\pi\circ \tilde F=F,\tilde F(0,t)=0$.
  
  考虑子空间 $A=I\times \set{0}\cup \set{0}\times I\cup \set{1}\times I$，$A$ 形如：
  
  根据定义，我们有 $F(A)=\set{1}\subseteq S^1$.
  
  由于 $\pi\circ \tilde F=F$，于是 $\tilde F(A)\subseteq\mathbb{Z}$。
  
  由于 $A$ 是连通的，有 $\tilde F(A)=\set{m}$，对于某个整数 $m$.
  
  由于 $\tilde F(0,t)=0$，有 $\tilde F(A)=\set{0}$.
  
  由于 $\tilde F(s,1)$ 是 $\pi\circ\gamma_n$ 的提升，根据道路提升的唯一性，有 $\tilde F(s,1)=\gamma_n$，于是 $n=\gamma_n(1)=\tilde F(1,1)=0$.
  
  于是 $\phi$ 是单射。

13. 基本群与同伦等价

圆周的基本群

回忆：圆周的基本群

$\pi_1(S^1)\cong \mathbb{Z}$.
应用：Brouwer 不动点定理 (Brouwer Fixed-Point Theorem)

考虑单位球 $B$，其维数为任意，考虑一个连续映射 $f:B\to B$，那么一定 $\exists x\in B$ 使得 $f(x)=x$.

证明：

我们这里只证明 $\text{dim}\leq 2$ 的情形，通常情况以后会学到。

首先看 $\text{dim}=1$ 的情形。

$B=[-1,1]\subset \mathbb{R}$. 这就是在说 $f:[-1,1]\to[-1,1]$ 连续，该映射有不动点。

考虑下图，

这就是在说橙色的函数图像与绿色对角线有交点。

假设 $f(x)\neq x$, $\forall x\in I$，那么令 $A=\set{x\in I\mid f(x)<x}$，$B=\set{x\in I\mid f(x)>x}$，那么有 $I=A\sqcup B$.

由于 $f(-1)\neq -1$，有 $f(-1)>-1$，且 $f(1)\neq 1$，有 $f(1)<1$.

因此 $A\neq \varnothing, B\neq \varnothing$.

我们考察 $A,B$ 集合的开闭性。令 $g(x)=f(x)-x$，有 $g:[-1,1]\to \mathbb{R}$ 且 $g$ 是连续映射。

于是 $A=g^{-1}(-\infty,0), B=g^{-1}(0,+\infty)$. 从而 $A,B$ 均为开集，这将连通的 $[-1,1]$ 区间分解为了两个非空开集的不交并，矛盾！

接着考察 $\text{dim}=2$ 的情形。

令 $D=\set{(x,y)\mid x^2+y^2\leq 1}$，这是一个二维的球。假设 $\exists f:D\to D$ 连续且 $\forall x\in D,f(x)\neq x$.

那么 $\forall x\in D$，考虑射线 $(f(x),x)$，延长直到射线与圆周 $S^1\subseteq D$ 相交。将与圆周的交点记作 $g(x)$.

那么 $g(x):D\to S^1$ 映射，如图所示：

由于 $f$ 是连续的，并且 $f(x)\neq x$，因此 $g$ 也是连续的。

并且若将 $g$ 限制在 $S^1$ 上，有 $g$ 是一个恒等映射，即 $g|_{S^1}=id|_{S^1}$。

如果我们考虑嵌入映射：$i:S^1\to D$，那么 $g\circ i:S^1\to D\to S^1$ 是恒等映射。

那么 $(g\circ i)_\star$（连续映射诱导的群同态）$=g_\star\circ i_\star=(id|_{S^1})_\star=id_{\pi_1(S^1)}$.

那么定有 $g_\star$ 是满射，但由于 $\pi_1(S^1)\cong\mathbb{Z}$，$D\subseteq \mathbb{R}^2$ 是一个凸集，这意味着 $\pi_1(D)$ 是一个平凡群 $\set{e}$，因此 $g_\star:\pi_1(D)\to \pi_1(S^1)$ 不可能是一个满射，矛盾。

基本群

单连通空间的判别

考虑 $X$ 中两个开集 $U,V$，使得 $X=U\cup V$. 如果 $U, V$ 都是单连通的（$\pi_1(U)=\pi_1(V)=\set{e}$，事实上，$U,V$ 此时是道路连通的），并假设 $U\cap V$ 是道路连通的，那么 $X$ 是单连通的，也就是 $\pi_1(X)=\set{e}$。

证明：

固定 $p\in U\cap V$，考虑环路 $\alpha:I=[0,1]\to X$ 拥有基础点 $p$.

那么 $I=[0,1]$ 也有一个开覆盖：$\alpha^{-1}(U)\cup \alpha^{-1}(V)$，由于 $I$ 是一个紧的度量空间，由 Lebesgue 引理，$\exists 0=t_0<t_1<\cdots<t_n=1$，使得 $[t_k,t_{k+1}]\subset\alpha^{-1}(U)$ 或 $\alpha^{-1}(V)$.

令 $\alpha_k(s)=\alpha((t_k-t_{k-1})\cdot s+t_{k-1}),s\in [0,1]$ （$\alpha$ 限制在 $[t_{k-1},t_{k}]$ 上），则 $\alpha_k(0)=\alpha(t_{k-1}),\alpha_k(1)=\alpha(t_k)$.

如果 $\alpha(t_k)\in U$，我们连接 $p$ 与 $\alpha(t_k)$，得到道路 $\gamma_k\subset U$.

同理，若 $\alpha(t_k)\in V$，我们连接 $p$ 与 $\alpha(t_k)$，得到道路 $\gamma_k\subset V$.

若 $\alpha(t_k)\in U\cap V$，我们连接 $p$ 与 $\alpha(t_k)$，得到道路 $\gamma_k\subset U\cap V$（由于 $U\cap V$ 道路连通，这可以做到）。

于是有 $\alpha\simeq(\alpha_1\gamma_1^{-1})(\gamma_1\alpha_2\gamma_2^{-1})\cdots(\gamma_{n-1}\alpha_n)\text{ rel}\set{0, 1}$.

如图所示，我们事实上是做了一个环路的分解。

括号中的每个环路都是 $U$ 或 $V$ 中的环路。由于 $U$ 与 $V$ 都是单连通区间，我们有 $\gamma_k\alpha_{k+1}\gamma_{k+1}^{-1}\simeq e\text{ rel}\set{0,1}$.

因此 $\alpha\simeq e\text{ rel}\set{0,1}$.

因此 $X$ 确实是单连通区域，$\pi_1(X)\cong \set{e}$。
高位球面的基本群是平凡群

高维球面 $S^n$ 的基本群是平凡群，即 $\pi_1(S^n)=\set{e}$ 若 $n\geq 2$。

证明：

令 $U=S^n\setminus\set{(1,0,0,\cdots,0)}$，$V=S^n\setminus\set{(-1,0,0,\cdots,0)}$.

我们有 $U,V$ 都是开集，且 $S^n=U\cup V$，有 $U, V$ 同胚于 $\mathbb{R}^n$，因此 $\pi_1(U)=\pi_1(V)=\set{e}$.

考察集合 $U\cap V$，它同胚于 $\mathbb{R}^n\setminus\set{0}$，当 $n\geq 2$ 时这是道路连通的空间。

因此 $\pi_1(S^n)$ 确实是平凡群。

（这个定理也解释了 $U\cap V$ 道路连通的必要性，因为当 $n=1$ 其他条件依然成立，但 $\mathbb{R}^1\setminus\set{0}$ 不是道路连通）
乘积空间的基本群同构于基本群的乘积

$\pi_1(X\times Y)\cong \pi_1(X)\times \pi_1(Y)$.

证明：

选择 $x_0\in X,y_0\in Y$，选 $(x_0,y_0)$ 作为基本点。考察 $p_1,p_2$ 为两个投影映射。

接下来我们构造一个群同态：令映射 $\phi:\pi_1(X\times Y)\to \pi_1(X)\times \pi_1(Y)$.

其中 $<\alpha>\to((p_1)_\star(<\alpha>),(p_2)_\star(<\alpha>))$，$\alpha$ 是 $(x_0,y_0)$ 处的环路。

我们想要验证这是一个同构。我们知道 $\phi$ 是一个群同态，只需验证其为单射、满射。

记 $e\in \pi_1(X\times Y), e_1\in \pi_1(X), e_2\in \pi_1(Y)$ 恒等元。

单射：

如果 $p_1\circ\alpha \underset{F}{\simeq} e_1\text{ rel}\set{0,1}, p_2\circ\alpha\underset{G}{\simeq} e_2\text{ rel}\set{0,1}$

那么 $\alpha\underset{(F,G)}{\simeq} e\text{ rel}\set{0,1}$，于是 $\phi$ 是一个单射。

满射：

令 $\alpha$ 是 $X$ 中环路，令 $\beta$ 是 $Y$ 中环路。

令 $\gamma(s)=(\alpha(s),\beta(s))$，那么有 $\gamma$ 是乘积空间中的环路，并且 $p_1\circ\gamma=\alpha,p_2\circ\gamma=\beta$.

根据定义，$\phi(<\gamma>)=(<\alpha>,<\beta>)$. 因此 $\phi$ 是一个满射。
- 例子：环面的基本群
  
  令 $T$ 是环面，我们知道 $T=S^1\times S^1$.
  
  从而 $\pi_1(T)=\mathbb{Z}^2$.

同伦等价 (Homotopy Equivalence)

回忆：同胚的概念

$X,Y$ 被称为是同胚的，如果 $\exists f:X\to Y,g:Y\to X$ 连续映射，且 $f\circ g=id_Y,g\circ f=id_X$。

注意到同胚的限制非常强，我们可否对这个限制进行放松？
定义：同伦等价 (Homotopy Equivalence)

我们将 $X,Y$ 称作是同伦等价 (Homotopy Equivalent)的，若 $\exists f:X\to Y,g:Y\to X$ 连续映射，且 $g\circ f\simeq id_X,f\circ g\simeq id_Y$.

此时 $f,g$ 被称为是同伦等价 (Homotopy Equivalence)，将 $f,g$ 称为是对方的同伦逆 (Homotopy Inverse).

此时也记作 $X\simeq Y$。

易知，$X\cong Y\Rightarrow X\simeq Y$.
同伦等价的基本性质
- 同伦等价是一个等价关系
  
  同伦等价是等价关系。
  
  证明：
  
  自反性：$id_X:X\to X$ 是一个同伦等价（这事实上是同胚），因此 $X\simeq X$.
  
  对称性：由定义这自然是对称的。
  
  传递性：若 $X\simeq Y,Y\simeq Z$，则 $\exists$ 下面的图表：
  
  其中 $g\circ f\simeq id_X,f\circ g\simeq id_Y$, $\phi\psi\simeq id_Z,\psi\phi\simeq id_Y$.
  
  于是 $g\circ \psi\circ \phi\circ f\simeq g\circ id_Y\circ f=g\circ f\simeq id_X$.
  
  $\phi\circ f\circ g\circ\psi\simeq \phi\circ id_Y\circ\psi=\phi\circ\psi\simeq id_Z$
  
  从而这是一个等价关系。
- 构造同伦等价的一个基本例子：形变收缩 (Deformation Retraction)
  
  $A\subset X$，假设 $\exists F:X\times I\to X$，有 $F(x,0)=x,F(x,1)\in A$，且 $F(x,t)=x$ 若 $x\in A$. 这意味着 $A$ 中的点对 $F$ 是不动点。则我们将 $F$ 称作是一个从 $X$ 到 $A$ 的形变收缩 (Deformation Retraction).
  
  直观上看，将 $F$ 看作一族从 $X$ 到 $X$ 的映射，这族映射从 $X$ 逐渐收缩到 $A$ 并保持 $A$ 中点不动。
  
  事实上，我们会有：$X\simeq A$.
  
  证明：
  
  考虑 $i:A\to X$ 是嵌入映射以及映射 $f(x)=F(x,1): X\to A$。
  
  一方面，我们有 $f\circ i=id_A$。
  
  另一方面，我们有 $i\circ f\underset{F}{\simeq} id_X$. 这是由于左侧为 $F(x,1)$，右侧为 $F(x,0)$，这直接给出了同伦。
- 可缩空间 (Contractable Space)
  
  我们称 $X$ 是可缩的 (Contractable)，若 $id_X$ 与某个常数映射 $p\in X$ 是同伦的。
  
  令 $i:p\to X$ 是嵌入映射，令 $f=c_p:x\to p$，那么 $f\circ i=id_p$，$i\circ f\simeq id_X$，因此 $X\simeq\set{p}$.
  
  换言之，可缩意味着空间在同伦意义上是平凡的。
  
  注：可缩并不意味着存在一个到单点的形变收缩，我们会在将来举例说明这一点。
同伦等价的例子
- 凸集是可缩的
  
  令 $X$ 是欧氏空间 $\mathbb{R}^n$ 中的凸集，则 $X$ 是可缩的。更进一步地，它可以形变收缩到一个点。
  
  证明：令 $x_0=X$，令 $F(x,t)=(1-t)x+tx_0$，则 $F(x,0)=x,F(x,1)=x_0$，这给出了一个 $X$ 上的形变收缩（直线收缩）。
- $\mathbb{R}^n\setminus\set{0}$ 可以形变收缩到 $S^{n-1}$
  
  $\mathbb{R}^n\setminus\set{0}$ 可以形变收缩到 $S^{n-1}$.
  
  证明：
  
  令 $F(x,t)=(1-t)x+t\cfrac{x}{|x|}$，则由于 $x\in \mathbb{R}\setminus\set{0}$，有 $|x|\neq 0$，故 $F$ 是良定义的。
  
  并且 $F(x,0)=x,F(x,1)=\cfrac{x}{|x|}\in S^{n-1}$，且有 $F(x,t)=x,\forall x\in S^{n-1}$.
  
  故这给出了一个形变收缩。
- 对圆柱进行形变收缩
  
  如图所示，可以将圆柱“压缩”成一个圆形。
  
  我们也可以用粘合映射来考察这一点：
  
  注：什么时候粘合与形变压缩可以交换？只要在压缩前后，本来应该粘合在一起的点仍然粘合在一起，本来没有粘合在一起的点仍然没有粘合在一起，那么这两个操作就是可以交换的。需要具体例子具体分析。
- 莫比乌斯带的同伦等价
  
  留作作业：我们将在作业中证明莫比乌斯带是 $\simeq S^1$ 的。

14. 同伦等价：进一步研究

同伦等价

形变收缩的例子
- 去掉一点环面的形变收缩
  
  $X$ 是环面，则 $X\setminus\set{p}\simeq S^1\cup S^1$
  
  考察粘合映射：
  
  如图，所有点都可以往边界上收缩直到边界，最终得到：
  
  从立体上看，这事实上也可以看成是构成环面的两个圆分别收缩：
- 去掉一点实射影平面的形变收缩
  
  $\mathbb{R}P^2\setminus\set{p}\simeq\mathbb{R}P^1=S^1$
  
  同样地，考虑粘合，我们同样可以把所有内部点收缩到边界：
  
  这事实上就是 $S^1/\mathbb{Z}_2=\mathbb{R}P^1=S^1$. 其中 $-1\cdot x = -x$.
同伦映射诱导的基本群同态基本相同

考虑 $f\underset{F}\simeq g:X\to Y$，则 $g_\star:\pi_1(X,p)\to \pi(Y,g(p))$，它等于如下映射的复合：$\pi_1(X,p)\xrightarrow{f_\star}\pi_1(X,f(p))\xrightarrow{\gamma_\star}\pi_1(Y,g(p))$，其中 $\gamma_\star$ 为交换标志点（基本点）的同构，$\gamma$ 是一条道路，$\gamma(s)=F(p,s)$，$\gamma_\star(<\alpha>)=<\gamma^{-1}\cdot\alpha\cdot\gamma>$.

证明：

选取 $\alpha$ 为 $X$ 中的环路，其基本点为 $p$.

我们想要证明，$g\circ\alpha\simeq \gamma^{-1}\cdot(f\circ \alpha)\cdot \gamma\text{ rel}\set{0,1}$.

我们构造映射 $G:I\times I\to Y$，其中 $G(s,t)=F(\alpha(s),t)$.

$G$ 的形状如下所示：

注意到我们想要证明的同伦就是正方形边界上的两条道路同伦。

令 $\beta_1:I\to I\times I$，$\beta_1=\begin{cases}(0,2s)&0\leq s\leq 1/2\\(2s-1,1)&1/2\leq s\leq 1\end{cases}$.

令 $\beta_2:I\to I\times I$，$\beta_2=\begin{cases}(2s,0)&0\leq s\leq 1/2\\(1,2s-1)&1/2\leq s\leq 1\end{cases}$.

由于正方形是一个凸集，并且 $\beta_1$ 与 $\beta_2$ 起点和终点一致，因此 $\beta_1\simeq\beta_2\text{ rel}\set{0,1}$.

因此 $\gamma\cdot(g\circ\alpha)=G\circ\beta_1\simeq G\circ\beta_2=(f\circ\alpha)\cdot\gamma\text{ rel}\set{0,1}$.

从而 $g\circ\alpha\simeq\gamma^{-1}\cdot(f\circ\alpha)\cdot\gamma\text{ rel}\set{0,1}$.

由此我们证明结论。
同伦等价空间的基本群相同（基本群是同伦不变量）

若 $X,Y$ 是同伦等价的空间，则 $\pi_1(X)\cong\pi_1(Y)$.

证明：

令 $f:X\to Y, g:Y\to X$ 是两个互为同伦逆的映射，即 $id_X\underset{F}\simeq g\circ f,id_Y\underset{G}\simeq f\circ g$.

固定 $p=g(q)\in X,q\in Y$，我们想要证明 $f_\star:\pi_1(X,p)\to \pi_1(Y,f(p))$ 是一个群同构。

考虑 $\gamma$ 是 $X$ 里的道路，其中 $\gamma(s)=F(p,s)$，由上面的定理，有 $(g\circ f)_\star=\gamma_\star:\pi_1(X,p)\to \pi_1(X,g\circ f(p))$（$\gamma_\star\circ id_{X\star}= (g\circ f)_\star$）

由于 $(g\circ f)_\star=g_\star\circ f_\star$ 是同构，有 $f_\star$ 是单射。

类似地，有 $(f\circ g)_\star:\pi_1(Y,q)\to \pi_1(Y,f\circ g(q))$ 是群同构，有 $f_\star$ 是一个满射。

因此 $f_\star$ 是一个双射，$f_\star$ 自然是同态，有 $f_\star$ 是同构。
形变收缩保持基本群

令 $A\subset X$ 是 $X$ 的子空间，$\exists$ 从 $X$ 至 $A$ 的形变收缩，则 $\pi_1(X)\cong\pi_1(A)$.

证明：由上面定理立得。
可缩空间的基本群是平凡群

若 $X$ 是可缩的，则 $\pi_1(X)\cong\set{e}$.

证明：由上面定理立得。
形变收缩的基本群

$\mathbb{R}^n\setminus\set{0}\simeq S^{n-1}$，因此 $\pi_1(\mathbb{R}^n\setminus\set{0})=\begin{cases}\mathbb{Z}&n=2\\\set{e}&n\geq 3\end{cases}$.

类似地，圆柱和莫比乌斯带的基本群都是 $\mathbb{Z}$.
可缩空间的基本性质

以下给出关于可缩空间的性质：
- 1. $X$ 是可缩的等价于 $X\simeq\set{p}$；
- 1. 考虑两个映射 $f,g:X\to Y$，其中 $Y$ 是一个可缩空间，则 $f\simeq g$；
- 1. $X$ 是可缩等价于 $id_X\simeq C_p,\forall p\in X$，其中 $C_p$ 是映射至 $p$ 的常数映射。
证明：
$(\Rightarrow)$: 显然；

$(\Leftarrow)$: 设 $X\xrightarrow{f}\set{p},\set{p}\xrightarrow{g}X$，那么 $g\circ f\underset{F}\simeq id_{X}$，于是 $F$ 给出了一个 $id_X$ 到常数映射 $C_q(q=g(p))$ 的同伦收缩，因此 $X$ 是可缩空间。
$f=id_Y\circ f\simeq C_p\circ f$，其中 $p\in Y,C_p$ 为常数映射。

而 $C_p\circ f=C_p\circ g\simeq id_Y\circ g=g$.

因此 $f$ 与 $g$ 同伦。
令 $id_X\simeq C_p$，$\forall x\in X$，由于 $X$ 是可缩空间，根据 (2) 我们有 $C_x\simeq C_p\simeq id_X$.
- 注：可缩与形变收缩到一个点并不等价
  
  令 $X$ 是可缩空间，$p\in X$，那么有可能出现 $\not\exists$ 从 $X$ 到 $\set{p}$ 的形变收缩。
  
  我们考虑如下反例：
  
  令 $X$ 是一个“梳子空间”，这是说 $X=([0,1]\times \set{0})\cup(\bigcup_{n=1}^{\infty}\set{\cfrac{1}{n}}\times[0,1])\cup( \set{0}\times [0,1])$，如下图所示：
  
  令 $p=(0,1)\in X$，则 $\not\exists$ 从 $X$ 至 $\set{p}$ 的形变收缩。
  
  这是易于理解的，因为一个到 $\set{p}$ 的形变收缩 $F:X\times I\to X$ 是一个整体连续的映射，我们考察 $F(-,t)$ 在 $(1,1),(1/2,1),(1/3,1),\cdots$ 的取值，它们是趋于点 $p$ 的，$F(p,t)=1$，这与这些点需要先回到 $x$ 轴上再移动到点 $p$ 矛盾。
Van-Kampen 定理 (Van-Kampen Theorem)

回忆：上节课我们学到，若 $X=U\cup V$ 开覆盖，$\pi_1(U)=\pi_1(V)=\set{e}$，$U\cap V$ 是道路连通，则 $\pi_1(X)=\set{e}$。

这个定理启示我们将 $X$ 分解为更小的空间。我们将进行推广，进而得到 Van-Kampen 定理。首先我们进行代数准备工作：
- 群的自由积 (Free Product of Groups)
  
  $G_1,G_2$ 是两个群，
  
  回忆：在抽象代数中我们学过直积 (Direct Product)，有 $G_1\times G_2=\set{(g_1,g_2)\mid g_1\in G_1,g_2\in G_2}$，乘法定义为 $(g_1,g_2)\cdot(g_1',g_2')=(g_1g_1',g_2g_2')$。
  
  上述定义的直积拥有这样的特点：考虑 $(g_1,e)\cdot(e,g_2)=(g_1,g_2)=(e,g_2)\cdot(g_1,e)$，也就是说直积中部分非平凡乘法是可交换的，就算 $G_1,G_2$ 是不可交换的。直积的定义给乘法的定义加了一些“可交换”的限制。
  
  我们接下来定义自由积 (Free Product)：$G_1\star G_2$.
  
  引入单词 (word)，一个单词是一个序列 $g_1g_2\cdots g_m$，使得 $g_i\in G_1$ 或 $G_2$.
  
  一个单词被称为是约化的 (Reduced)，若：
  - 1. $\forall g_i$，$g_i$ 不是 $G_1$ 或 $G_2$ 的恒等元；
  - 1. $\forall$ 相邻的元素 $g_i$ 与 $g_{i+1}$，有 $g_i,g_{i+1}$ 属于不同的群 $G_1,G_2$. ($g_i\in G_1\Rightarrow g_{i+1}\in G_2$, $g_i\in G_2\Rightarrow g_{i+1}\in G_1$)
  理解上看，约化可以被理解为这个序列在某种意义上是不可简化的，也就是不能去掉单位元，不能把相邻元素乘起来。
  
  我们定义 $G_1\star G_2=\set{\text{约化的单词}}$，定义乘法：$(g_1g_2\cdots g_m)\cdot(h_1h_2\cdots h_n)= (g_1\cdots g_mh_1\cdots h_n) \text{ 约化后的结果}$，我们来解释“约化后的结果”一词的意思：
  
  若 $g_m,h_1$ 属于同一个群，那么我们考虑新的单词 $(g_1\cdots g_{m-1}(g_mh_1)h_2\cdots h_n)$；
  
  此时，若 $g_mh_1=e$，则我们删去 $(g_mh_1)$，即考虑 $(g_1\cdots g_{m-1}h_2\cdots h_n)$ 回到第一步进行约化；
  
  若 $g_mh_1\neq e$，约化结束，得到约化结束的单词。
  
  若 $g_m,h_1$ 属于不同的群，我们不需要进行约化，得到约化结束的单词。
  
  可以说明，经过有限多步之后，我们得到了一个约化后的单词，我们将这个单词称为约化前两个元素的乘积。
  
  定义单位元：空单词；
  
  定义逆元：$(g_1,\cdots g_m)^{-1}=(g_m^{-1}\cdots g_1^{-1})$.
  
  我们可以验证，我们得到了一个群结构 $G_1\star G_2$，将其称作 $G_1$ 与 $G_2$ 的自由积。
  
  进一步推广，我们可以考虑指标集 $I$ 关联的群的自由积：
  
  定义 $\underset{_{\alpha\in I}}{\large\star} G_\alpha$ 为所有约化的单词 $g_1\cdots g_m$ 使得 $g_i\in G_{\alpha_i}$，乘法与逆元同上定义。（需要注意，尽管指标集可以是无限群，但是单词的长度都是有限的）
  
  如果 $G_\alpha\cong \mathbb{Z},\forall \alpha$，则 $\underset{_{\alpha\in I}}{\large\star} G_\alpha$ 称作一个自由群 (Free group)。
  
  对自由积有如下泛性质：
  - 自由积的泛性质 (Universal Property)
    
    $\forall \alpha$，我们都有嵌入映射 $i_\alpha:G_\alpha\to \underset{_{\alpha\in I}}{\large\star} G_\alpha$，其中 $g\to g,g\neq e$，$e\to \text{空单词}$.
    
    假设给定一些群同态 $\varphi_\alpha:G_\alpha\to H,\forall \alpha$，其中 $H$ 是一个固定好的群，那么 $\exists!$ 群同态 $\varphi:\underset{_{\alpha\in I}}{\large\star} G_\alpha\to H$，使得 $\varphi\circ i_\alpha=\varphi_\alpha$. 这即是如下的交换图表：
    
    证明：
    
    令 $g_1\cdots g_m\in \underset{_{\alpha\in I}}{\large\star} G_\alpha$，定义 $\varphi(g_1\cdots g_m):=\varphi_{\alpha_1}(g_1)\cdots \varphi_{\alpha_m}(g_m)$，这便得到了唯一的合理映射。
考虑拓扑空间 $X$，它有一个开覆盖 $\bigcup_\alpha A_\alpha$，若 $\exists x_0\in \bigcap_\alpha A_\alpha$，考虑嵌入 $i_\alpha:A_\alpha\to X$，则有诱导的基本群群同态：$i_{\alpha\star}:\pi_1(A_\alpha,x_0)\to\pi_1(X,x_0)$.

由上面的泛性质，有 $\exists !\phi:\underset{_{\alpha}}{\large\star} \pi_1(A_\alpha,x_0)\to \pi_1(X,x_0)$，使得 $\phi|_{\pi_1(A_\alpha,x_0)}=i_{\alpha\star}$.
- Van-Kampen 定理 (Van-Kampen Theorem)
  
  令 $X=\bigcup_\alpha A_\alpha$ 开覆盖，$\exists x_0\in \bigcap_\alpha A_\alpha$，如果 $A_\alpha$ 以及 $A_\alpha\cap A_\beta$ 是道路连通 $\forall \alpha,\beta$，则考虑 $\phi:\underset{_{\alpha}}{\large\star} \pi_1(A_\alpha,x_0)\to \pi_1(X,x_0)$，它是一个满射；
  
  若进一步假设 $A_\alpha\cap A_\beta\cap A_\gamma$ 也都是道路连通，$\forall \alpha,\beta,\gamma$，则 $\ker \phi$ 是正规子群 $N$，且正规子群 $N$ 由下面这些元素生成：$((i_{\alpha\beta})_\star (w)) ((i_{\beta\alpha})_\star (w))^{-1}$，其中 $i_{\alpha\beta}: A_\alpha\cap A_\beta\to A_\alpha$ 嵌入映射，$i_{\beta\alpha}:A_\beta\cap A_\alpha\to A_\beta$ 嵌入映射，$w$ 是 $A_\alpha\cap A_\beta$ 中环路。
  
  解释：直观上看，$w$ 是 $A_\alpha\cap A_\beta$ 中的环路，这是将环路先看作 $A_\beta$ 中的环路，再将环路看作 $A_\alpha$ 中的环路并相乘，这最终是将这些环路看作 $X$ 中的环路然后相乘。

15. Van-Kampen 定理

Van-Kampen 定理

回忆：Van-Kampen 定理 (Van-Kampen Theorem)

令 $X=\bigcup_\alpha A_\alpha$ 开覆盖，$\exists x_0\in \bigcap_\alpha A_\alpha$，则有：
1. 若 $A_\alpha\cap A_\beta,A_\alpha,A_\beta$ 都是道路连通 $ ,$，则 $\phi:\underset{_{\alpha}}{\large\star}\pi_1(A_\alpha,x_0)\to \pi_1(X,x_0)$ 是一个满射。
2. 若进一步假设 $A_\alpha \cap A_\beta\cap A_\gamma$ 是道路连通，$\forall \alpha,\beta,\gamma$，则 $\ker \phi$ 是一个正规子群 $N$，有 $N$ 由下面这些元素生成：$((i_{\alpha\beta})_\star(w))((i_{\beta\alpha})_\star(w))^{-1}$，其中 $i_{\alpha\beta}$ 与 $i_{\beta\alpha}$ 是嵌入映射，分别表示 $A_\alpha\cap A_\beta$ 嵌入 $A_\alpha$ 与 $A_\beta$。
回忆：单连通的判别定理（Van-Kampen 定理的特例）

令 $X=A_1\cup A_2$，且 $A_1,A_2$ 为单连通，$A_1\cap A_2$ 道路连通。

由 Van-Kampen，有 $\pi_1(A_1,x_0)\star \pi_1(A_2,x_0)\to \pi_1(X,x_0)$ 是一个满射，前两个群是平凡群，因此 $\pi_1(X)$ 是一个平凡群。
例：八字形的基本群

令 $S^1\bigvee S^1=X$ 是两个 $S^1$ 的 Wedge Sum，假设粘合点为 $x_0$.

我们令 $A_1$ $A_2$ 如图取值：

从而 $A_1,A_2$ 开集（不能直接取圆周是因为圆周不是开集），有 $X=A_1\cup A_2$，并且 $A_1\cap A_2$ 是一个可缩空间，因此其为平凡空间。我们有 $A_1\simeq S^1,A_2\simeq S^1$.

由 Van-Kampen 定理，有 $\pi_1(X,x_0)=\pi_1(A_1,x_0)\star \pi_1(A_2,x_0)$，因此 $\pi_1(X,x_0)\simeq \pi_1(S^1)\star \pi_1(S^1)\simeq Z\star Z$.
例：多个空间 Wedge Sum 的基本群

令 $x_\alpha\in X_\alpha,\alpha\in I$，令 $X=\bigvee_\alpha X_\alpha$ 是所有空间的 Wedge Sum，也就是说 $X$ 是 $\bigsqcup_\alpha X_\alpha$ 的粘合空间，其中 $x_\alpha$ 被粘合。

假设 $\forall \alpha$，$\exists$ 邻域 $U_\alpha\subseteq X_\alpha$，使得 $\exists$ 形变收缩 $U_\alpha\to \set {x_\alpha}$，令 $A_\alpha=X_\alpha \bigvee_{\beta\neq\alpha}U_\beta$，则有 $A_\alpha$ 在 $X$ 中是开集，且 $A_\alpha\cap A_\beta=A_\alpha\cap A_\beta\cap A_\gamma=\bigvee_\alpha U_\alpha$，其中 $\alpha\neq\beta$.

我们知道 $\bigvee_\alpha U_\alpha$ 可以形变收缩到 $\set{x_\alpha}$，于是它是一个可缩空间，基本群平凡，于是 $\ker \phi=\set{e}$，于是 $\pi_1(X)\cong \underset{_{\alpha}}{\large\star}\pi_1(X_\alpha)$.
Van-Kampen 定理的证明 (Hatcher)
- Step 1. 证明映射 $\phi$ 是满射
  
  令 $f:I\to X$ 是一个环路，其基本点为 $x_0$. 考虑区间 $[0,1]$ 有一个开覆盖 $\bigcup_\alpha f^{-1}(A_\alpha)$.
  
  由于 $[0,1]$ 是紧的度量空间，根据 Lebesgue 引理，$\exists$ 分划 $0=s_0<s_1<\cdots<s_n=1$，使得对某一个 $\alpha$ 有 $[s_i,s_{i+1}]\subseteq f^{-1}(A_\alpha), \forall i$.
  
  考虑记 $A_i$ 为其包含了 $f([s_{i-1},s_{i}])$ 的 $A_\alpha$，令 $f_i(s)=f((s_i-s_{i-1})s+s_{i-1}),s\in [0,1]$ （考虑中间的一小段道路）。
  
  由于 $f(s_i)\in A_i\cap A_{i+1}$，选择道路 $g_i$ 位于 $A_i\cap A_{i+1}$ 中，其中起点为 $x_0$，终点为 $f(s_i)$ （这是因为开集的交是道路连通），于是 $f\simeq (f_1\cdot g_1^{-1})(g_1 f_2 g_2^{-1})\cdots (g_{n-1}f_n)\text{ rel}\set{0,1}$，于是 $f$ 被分解成了若干个环路的乘积，并且每一个环路都落在某个 $A_i$ 中。
  
  因此，$\phi$ 是一个满射。
- Step 2. 证明 $\ker \phi=N$
  
  我们首先引入分解 (Factorization)的概念：
  
  我们称一个 $[f]\in \pi_1(X,x_0)$ 的分解（注：$[f]$ 即为之前的 $<f>$，即 $f$ 对应的同伦类，后同）为一个乘积 $[f_1][f_2]\cdots [f_k]$ 使得如下成立：
  1. $f_i$ 是某一个 $A_\alpha$ 里的环路，且其基本点位于 $x_0$；
  2. 在 $X$ 中有 $f\simeq f_1f_2\cdots f_k\text{ rel}\set{0,1}$.
  给出一个分解，则我们设 $[f_1]\cdots [f_k]\in \underset{_{\alpha}}{\large\star}\pi_1(A_\alpha,x_0)$，有 $\phi([f_1]\cdots [f_k])=[f]$。
  
  考虑 $[f]$ 的两个分解，两个分解被称为是等价的如果它们可以被如下的操作或者操作的逆联系起来：
  1. 如果 $[f_i]$ 与 $[f_{i+1}]$ 落在同一个 $\pi_1(A_\alpha,x_0)$ 中，则将 $[f_i],[f_{i+1}]$ 组合为 $[f_i \cdot f_{i+1}]$.
  2. 如果 $f_i$ 是 $A_\alpha\cap A_\beta$ 中的环路，则将 $[f_i]\in \pi_1(A_\alpha,x_0)$ 看作 $[f_i]\in \pi_1(A_\beta,x_0)$.
  由 $N$ 的定义，我们知道等价的分解会给出下面这个商群中的相同元素：$Q:=\underset{_{\alpha}}{\large\star}\pi_1(A_\alpha,x_0)/N$. 我们希望证明 $[f]$ 的任意两个分解都是等价的，这意味着 $Q\to \pi_1(X,x_0)$ 是一个单射，换言之 $\ker \phi=N$.
  
  接下来我们来证明这一点：
  
  给出两个分解 $[f]=[f_1]\cdots[f_k]=[f_1']\cdots[f_l']$，有 $f_1\cdots f_k\simeq f_1'\cdots f_l'\text{ rel}\set{0,1}$.
  
  根据同伦的定义，$\exists F:I\times I\to X$ 是一个 $f_1\cdots f_k$ 至 $f_1'\cdots f_l'$ 的同伦。
  
  对正方形的开覆盖 $I\times I\subset \bigcup_\alpha F^{-1}(A_\alpha)$，由于正方形是紧的度量空间，根据 Lebesgue 引理我们有 $\exists 0=s_0<\cdots <s_m=1,0=t_0<\cdots<t_n=1$，使得每一个小矩形 $R_{ij}:=[s_{i-1},s_i]\times [t_{i-1},t_i]\subseteq F^{-1}(A_\alpha)$ 对于某个 $\alpha$.
  
  为了记号的方便，我们记作 $R_{ij}\subseteq F^{-1}(A_{ij})$。
  
  考虑分划 $0=s_0<\cdots<s_m=1$，我们总可以假设这个分划是 $f_1\cdots f_k$ 与 $f_1'\cdots f_l'$ 的加细。同时我们也假设 $n\geq 3$.
  
  我们对分解做一个小的扰动，将 $R_{ij}$ 竖直边做扰动使得正方形中的每一个点都落在至多三个 $R_{ij}$ 中。我们重新将扰动后的矩形记作 $R_1R_2\cdots R_{mn}$.
  
  如图所示，需要注意我们保持最上面和最下面的竖边不动，这也解释了为什么我们要假设 $n\geq 3$.
  
  令 $\gamma_p$ 为将 $R_1\cdots R_p$ 与 $R_{p+1}\cdots R_{mn}$ 分开的道路。
  
  于是 $F\circ \gamma_p$ 是一个 $x_0$ 处的环路。
  
  我们将 $R_p$ 的角称作顶点 (Vertex)，对于每一个使得 $F(v)\neq x_0$ 的顶点我们选取道路 $g_v$ 使得 $g_v$ 连接了 $x_0$ 与 $F(v)$，且 $g_v$ 落在所有包含了 $v$ 的 $R_{p}$ 所对应的 $A_{ij}$ 的交集中（由于我们先前做了扰动，这一定是两个或三个 $A_{ij}$，根据假设，这个交集是道路连通的，所以 $g_v$ 可以取到）。
  
  由此，我们可以从 $F\circ \gamma_p$ 诱导一个分解，将 $g_v^{-1}\cdot g_v$ 加在相邻的顶点间，从而可以得到一个分解（形式上地讲，这比较像是 Step1 中的环路乘积，如下图是一个由 $F\circ \gamma_5$ 诱导的分解）。
  
  此外，$F\circ \gamma_p$ 与 $F\circ \gamma_{p+1}$ 是同伦的，并且该同伦可以仅仅局限于 $R_{p+1}$ 所对应的 $A_{ij}$ 上（如下图），因此 $F\circ \gamma_p$ 与 $F\circ \gamma_{p+1}$ 这两个分解是等价的。
  
  如图所示，$F\circ \gamma_5$ 与 $F\circ \gamma_6$ 只在 $R_6$ 中出现区别，因此它们能在 $R_6$ 对应的 $A_{ij}$ 中定义一个同伦，因此 $F\circ \gamma_5$ 与 $F\circ\gamma_6$ 给出等价的分解。
  
  最后，$F\circ\gamma_0$ 能被分解为等价于 $[f_1]\cdots [f_k]$ 的分解，证明如下：
  
  我们先前已经假设过了 $0=s_0<\cdots<s_m=1$ 是一组关于 $[f_1]\cdots [f_k]$ 的加细分化，因此考虑矩形底边的每一个顶点 $v$，它有两种情形：
  
  第一，若该顶点 $v$ 位于某个 $[f_p]$ 对应的区间内部，此时不妨设 $[f_p]\in \pi_1(A_p)$，则我们取 $g_v$ 落在 $A_p$ 以及所有包含了 $v$ 的矩形 $R_q$ 所对应的 $A_{ij}$ 的交集中。其中 $g_v$ 连接了 $x_0$ 与 $v$。由于 $v$ 在底边上，包含 $v$ 的矩形至多只有两个，所以交集至多只是三个集合的交，由假设我们有该交集道路连通，因此 $g_v$ 是良好定义的；（如下图所示）
  
  第二，若该顶点落于两个 $[f_p]$ 与 $[f_{p+1}]$ 对应的区间交点，此时一定有 $F(v)=x_0$，在构造分解时我们就不需要插入道路 $g_v$.
  
  类似上面从 $F\circ \gamma_p$ 诱导出分解地，我们从 $F\circ \gamma_0$ 诱导出了一个分解。要说明这个分解与 $[f_1]\cdots [f_k]$ 等价，我们只需要说明 $[f_i]$ 对应区间内的那段分解与 $[f_i]$ 是等价的。
  
  这自然成立，因为在我们构造出的分解中，位于 $[f_i]$ 区间内部的每个顶点 $v$ 总有 $g_v\subset A_i$，因此 $[f_i]$ 区间中的所有环路都可以看成是位于 $A_i$ 中的环路，它们的乘积于是是 $[f_i]$。
  
  综上，我们构造出了一个 $F\circ \gamma_0$ 诱导的与 $[f_1]\cdots [f_k]$ 的等价分解。
  
  类似地，我们也可以说明 $F\circ \gamma_{mn}$ 可以诱导一个等价于 $[f_1']\cdots [f_l']$ 的分解。因此由归纳法，由于 $F\circ \gamma_p$ 诱导出的分解等价于 $F\circ \gamma_{p+1}$，$\forall p$，有 $[f_1]\cdots [f_k]$ 等价于 $[f_1']\cdots [f_l']$.
  
  由此，我们完成了对 Van-Kampen 定理的证明。
例：Van-Kampen 定理计算环面基本群

令 $X$ 是一个环面，我们对其作如图分解：

图中的 $A_1,A_2$ 组成了一个环面的开覆盖，且 $A_1\simeq \set{e}$，有 $\pi_1(A_1)=\set{e}$.

$A_2\simeq S^1\bigvee S^1$，有 $\pi_1(A_2)=\mathbb{Z}_a\star \mathbb{Z}_b$.

对 $A_1\cap A_2$，有 $A_1\cap A_2\simeq S^1$，于是 $\pi_1(A_1\cap A_2)=\mathbb{Z}\cdot<\gamma>$，其中 $\gamma$ 为一个生成元。

由 Van-Kampen，考虑映射 $i_{12}:A_1\cap A_2\to A_1$，有 $(i_{12})_\star(<\gamma>)=e\in \pi_1(A_1)$.

考虑映射 $i_{21}:A_1\cap A_2\to A_2$，有 $(i_{12})_\star(<\gamma>)=aba^{-1}b^{-1}\in \pi_1(A_2)$

于是 $\pi_1(X)=<a,b\mid aba^{-1}b^{-1}>\simeq \mathbb{Z}\times \mathbb{Z}$

等价的解释： $\pi_1(X)$ 中有 $aba^{-1}b^{-1}=e$，即有 $ab=ba$.

注：记号 $<>$ 为一个群的表示 (Presentation)，该记号的一般性定义如下：
- 群的表示 (Presentation)
  
  对任意一个群 $G$，我们都可以将其记作 $G=<\text{生成元}\mid \text{关系}>=<g_\alpha\in G,\alpha\in I\mid h_\beta\in \underset{_{\alpha}}{\large\star} \mathbb{Z}_{g_\alpha},\beta\in J>=\underset{_{\alpha}}{\large\star}\mathbb{Z}_{g_\alpha}/N$
  
  其中 $N$ 为 $\set{h_\beta\mid \beta\in J}$ 生成的正规子群。
  
  特殊情况：$<g_\alpha\in G,\alpha\in I\mid \varnothing>=\underset{_{\alpha}}{\large\star}\mathbb{Z}_{g_\alpha}$ 为自由群.
例：Van-Kampen 定理计算克莱因瓶基本群

令 $X=\text{Klein Bottle}$.

同理有 $\pi_1(A_1)=\set{e}$，$A_2\simeq S^1\bigvee S^1$，于是 $\pi_1(A^2)=<a,b\mid\varnothing>$.

由 $\pi_1(A_1\cap A_2)=\mathbb{Z}\cdot<\gamma>$.

考虑嵌入 $(i_{12})_\star(<\gamma>)=e$，且 $(i_{21})_\star(<\gamma>)=aba^{-1}b$.

于是 $\pi_1(X)=<a,b\mid aba^{-1}b>$.

16. 覆叠空间：定义

Van-Kampen 定理计算基本群

例：实射影平面的基本群

令 $X=\mathbb{R}P^2$。

如图，类似之前地，我们有 $\pi_1(A_1)=\set{e}$.

对于 $A_2$，我们可以将其形变收缩至边界，这就是将圆周的对径点粘在一起，所得仍然是圆周，因此 $A_2\simeq S^1$，即 $\pi_1(A_2)=\mathbb{Z}\cdot a$. （$a$ 为 $\pi_1(A_2)$ 中生成元）

即如图：

同时，我们有 $\pi_1(A_1\cap A_2)=\mathbb{Z}\cdot <\gamma>$.

我们有 $(i_{12})_\star(\gamma)=e\in \pi_1(A_1)$，$(i_{21})_\star(\gamma)=a^2$.

从而 $\pi_1(X)=<a\mid a^2>\cong \mathbb{Z}/2\mathbb{Z}$.
例：亏格为 $g$ 可定向闭曲面

令 $X=\Sigma_g$，即亏格为 $g$ 且可定向的闭曲面。这是在说下图：

我们应该怎么粘合出这样一个曲面呢？先看 $g=2$ 的情形：

取一个固定点 $p$，我们可以取出如下圆周：

形式上讲，$A_i$ 是绕着第 $i$ 个洞“竖着”转一圈，$B_i$ 表示“横着”转一圈。

这可以怎么写成粘合形式呢？我们看八边形：

将该八边形粘合后即可得到上面的“两个洞的环面”。

我们可以做推广，对于亏格为 $g$ 的曲面，我们可以得到一个 $4g$ 边形形如：

粘合后，这个 $4g$ 边形的所有顶点即为我们此前固定的 $p$ 点。

由于我们得到了粘合之前的图，我们可以用类似挖洞的方法去计算基本群。

我们有：$\pi_1(X_1)=\set{e}$，$X_2\simeq\bigvee_{i=1}^{2g}S^1$，其中 $2g$ 个圆周即为 $A_i,B_i$，它们的粘合点就是先前固定的 $p$.

不妨记第 $i$ 组圆周为 $a_i,b_i$，从而 $\pi_1(X_2)=<a_1,b_1,\cdots,a_g,b_g\mid \varnothing>\cong \large{\star}_{i=1}^{2g}\mathbb{Z}$.

设 $\pi_1(X_1\cap X_2)=\mathbb{Z}\cdot<\gamma>$，有 $(i_{12})_\star(<\gamma>)=e\in \pi_1(X_1)$，$(i_{21})_\star(<\gamma>)=\prod_{i=1}^{g}a_ib_ia^{-1}_ib^{-1}_i$.

根据 Van-Kampen，有 $\pi_1(X)=<a_1,b_1,\cdots,a_b,b_g\mid \prod_{i=1}^{g}a_ib_ia^{-1}_ib^{-1}_i>$.

因此，当 $g_1\neq g_2$，有 $\pi_1(\Sigma_{g_1})\neq \pi_1(\Sigma_{g_2})$.

因此，$\Sigma_{g_1}$ 与 $\Sigma_{g_2}$ 不是同胚. 这是著名的曲面分类定理。
例：平凡纽结补集的基本群

$S^1=\set{(x,y,0)\in\mathbb{R}^3\mid x^2+y^2=1}$，考察 $X=\mathbb{R}^3\setminus S^1$.

首先有 $X\simeq B\setminus S^1$，其中 $B$ 是一个三维空间里包含了 $S^1$ 的球。

可以注意到，按如图所示方式画圈（想象球形空间里形如磁感线的曲线），只有穿过 $S^1$ 中心的竖线是不闭合的。

我们将这些圈“向外”收缩，收缩完成后就只剩下了球中间的直径以及单位球面。

进一步收缩直径的两个端点，如图所示，我们最终有 $X\simeq S^1\vee S^2$.

因此，$\pi_1(X)=\pi_1(S^2\vee S^1)=\pi_1(S^1)\star \pi_1(S^2)=\mathbb{Z}\star \set{e}=\mathbb{Z}$.

覆叠空间 (Covering Space)

回忆：计算圆周的基本群

我们在计算圆周的基本群时，我们构造了映射 $\pi:\mathbb{R}^1\to S^1$，$\pi(x)=e^{2\pi ix}$.

令 $U=S^1\setminus\set{-1}$，$V=S^1\setminus\set{1}$，有 $\set{U,V}$ 是 $S^1$ 的开覆盖。

我们有 $\pi^{-1}(U)=\bigsqcup_{n\in \mathbb{Z}} (n-1/2,n+1/2)$，$\pi^{-1}(V)=\bigsqcup_{n\in\mathbb{Z}} (n,n+1)$ 并且 $\pi|_{(n-1/2,n+1/2)}$ 诱导了一个 $(n-1/2,n+1/2)$ 与 $U$ 的同胚，$\pi|_{(n,n+1)}$ 诱导了一个 $(n,n+1)$ 与 $V$ 的同胚。

我们用这样形式的开覆盖去计算出了圆周的基本群，接下来我们扩展这个概念。
覆叠空间 (Covering Space)

底空间 $X$ 的覆叠空间 (Covering Space) 是一个空间 $\tilde X$ 以及一个连续映射 $p:\tilde X\to X$ 满足：

$\exists$ 底空间 $X$ 的开覆盖 $\bigcup_\alpha U_\alpha$，使得 $\forall \alpha$，$p^{-1}(U_\alpha)$ 可以表示为开集的不交并 $\bigsqcup_{\beta}V_{\alpha\beta}$，$V_{\alpha\beta}\subseteq \tilde X$ 开集且使得 $p|_{V_{\alpha\beta}}$ 给出了一个 $V_{\alpha\beta}$ 与 $U_\alpha$ 的同胚 $\forall \beta$。

此时我们称 $\tilde X$ 称作是覆叠空间，称 $p$ 是覆叠映射。
例：去心复数域的覆叠空间

令 $p:\mathbb{C}\to\mathbb{C}^\star(\mathbb{C}^\star=\mathbb{C}\setminus \set{0})$， $p(z)=e^z$。

令 $U=\mathbb{C}^\star\setminus \mathbb{R}_{<0}$，$V=\mathbb{C}^\star\setminus\mathbb{R}_{>0}$. 那么有 $U\cup V$ 构成了 $\mathbb{C}^\star$ 的开覆盖，并且：

$p^{-1}(U)=\bigsqcup_n V_{1n}$，其中 $V_{1n}=\set{z\in\mathbb{C}\mid(2n+1)\pi< \text{Im} z<(2n+3)\pi}$.

$p^{-1}(V)=n V{2n} $，其中 $V_{2n}=\set{z\in\mathbb{C}\mid 2n\pi<\text{Im} z<2(n+1)\pi}$.

且 $p|_{V_{1n}}:V_{1n}\to U$ 同胚，$p|_{V_{2n}}:V_{2n}\to V$ 同胚。

于是 $p$ 是覆叠映射。
例：另一个 $S^1$ 的覆叠空间

令 $p:S^1\to S^1$，$p(z)=z^n (n\geq 1)$，那么有 $p$ 是一个覆叠映射。

证明：

令 $U=S^1\setminus\set{-1},V=S^1\setminus\set{1}$.

则 $p^{-1}(U)=\set{e^{i\theta}\mid -\pi/n+(2k\pi)/n<\theta<\pi/n+(2k\pi)/n, 0\leq k\leq n-1}=\bigsqcup_{k=0}^{n-1}V_{1k}$

$p^{-1}(V)=\set{e^{i\theta}\mid (2k\pi)/n<\theta<(2\pi)/n+(2k\pi)/n,0\leq k\leq n-1}=\bigsqcup_{k=0}^{n-1}V_{2k}$.

同时也有 $p|_{V_{1k}}:V_{1k}\to U$ 同胚，$p|_{V_{2k}}:V_{2k}\to V$ 同胚。

因此 $p$ 是覆叠映射。

今后我们将会说明，以 $S^1$ 作为底空间，其覆叠空间只能长成 $S^1$ 或 $\mathbb{R}^1$ 的形式。
例：$S^1\vee S^1$ 的覆叠空间

令 $X=S^1\vee S^1$，那么它的覆叠空间可以长成如下形式：

如图为 $\tilde X$，这是一张有向图。令 $p:\tilde X\to X$，$p$ 将所有的有向图顶点映射至 $x_0$，将 $a$ 映射至 $a$，$b$ 映射至 $b$。

可以验证，$p$ 确实是一个覆叠空间。

不仅仅是如此，$\tilde X$ 还可以长成这样：

更一般性地，如果一张有向图满足每个点度数为 $4$，且恰有一个 $a$ 出度、一个 $a$ 入度、一个 $b$ 出度、一个 $b$ 入度，则该图可以看成是一个 $X$ 的覆叠空间。

我们描述一个叫做“万有覆叠空间”的概念，即它是一个 $X$ 的覆叠空间但没有环路，最终该空间 $X$ 的万有覆叠空间为：

这在形状上看是一个无限网格，并且它没有环路，有 $\pi_1(\tilde X)=\set{e}$.
道路提升引理 (Path-Lifting Lemma)

令 $p:\tilde X\to X$，$\tilde X$ 是覆叠空间，道路 $\gamma:I\to X$ 有 $\gamma(0)=x_0\in X$，令 $\tilde x_0\in \tilde X$ 有 $p(\tilde x_0)=x_0$，则 $\exists!\tilde\gamma:I\to\tilde X$，有 $\tilde\gamma(0)=\tilde x_0$，且 $p\circ\tilde\gamma=\gamma$.

证明：

令 $X=\bigcup_{\alpha}U_\alpha$ 是一个开覆盖，使得 $p^{-1}(U_\alpha)=\bigsqcup_{\beta} V_{\alpha\beta}$，且 $p|_{V_{\alpha\beta}}:V_{\alpha\beta}\to U_\alpha$ 同胚。

由于 $I$ 是一个紧的度量空间，由 Lebesgue Lemma，$\exists 0=s_0<s_1<\cdots<s_n=1$，使得 $[s_i,s_{i+1}]$ 都落在某一个 $\gamma^{-1}(U_{\alpha})$ 中。

令 $x_0\in U_{\alpha_0}$，令 $\tilde x_0\in V_{\alpha_0\beta_0}$，令 $\tilde \gamma(s)=(p|_{V_{\alpha_0\beta_0}})^{-1}\circ \gamma(s)$. 可以说明这是这一段小区间唯一的提升。

对指标做归纳法，有每一段小区间都存在唯一的提升，因此整体上有唯一提升。

由此证明了道路提升引理。
同伦提升引理 (Homotomy Lifting Lemma)

考虑映射 $p:\tilde X\to X$ 是一个覆叠映射，考虑 $F:Y\times I\to X$ 同伦映射，令 $\tilde f:Y\to \tilde X$ 满足 $p\circ \tilde f(Y)=F(y,0),\forall y\in Y$. 那么 $\exists! \tilde F:Y\times I\to\tilde X$，使得 $\tilde F(y,0)=F(y,0)$，且 $p\circ \tilde F=F$.

证明：

与此前的同伦提升引理不同，这一次我们失去了紧空间的性质。我们只说明证明的开头。

我们考虑 $\set{y_0}\times I$，这是一个紧的度量空间，因此 $\forall t\in I$，$\exists t\in(a_t,b_t)\subseteq [0,1]$，$\exists N_t\subseteq Y$ 为 $y_0$ 邻域，且 $F(N_t\times (a_t,b_t))\subseteq U_\alpha$ 对某个 $U_\alpha$.

17. 覆叠空间：提升

覆叠空间 (Covering Space)

同伦提升引理 (Homotopy Lifting Lemma)

考虑映射 $p:\tilde X\to X$ 是一个覆叠映射，考虑 $F:Y\times I\to X$ 同伦映射，令 $\tilde f:Y\to \tilde X$ 满足 $p\circ \tilde f(Y)=F(y,0),\forall y\in Y$. 那么 $\exists! \tilde F:Y\times I\to\tilde X$，使得 $\tilde F(y,0)=F(y,0)$，且 $p\circ \tilde F=F$.

证明：

固定 $y_0\in Y$，考虑 $\set{y_0}\times I$，有这是一个紧的度量空间。

$\forall t\in [0,1]$，$\exists (a_t,b_t)$ 有 $t\in (a_t,b_t)$，且 $\exists N_t\subseteq Y$，有 $y_0\in N_t$ 邻域，使得 $F(N_t\times (a_t,b_t))\subseteq U_\alpha$ 对某 $\alpha$. (连续性)

由于 $\set{y_0}\times I\subset \bigcup_{t\in [0,1]}N_t\times (a_t,b_t)$，这是一个开覆盖，$\exists 0=t_0<t_1<\cdots<t_m=1$，有 $\set{y_0}\times I\subset \bigcup_{i=0}^m N_{t_i}\times (a_{t_i},b_{t_i})$. (紧性)

令 $N_{y_0}=\bigcap_{i=0}^mN_{t_i}$，它是一个开集。（这里，取开集的意义是根据曾经学过的连续性判别方法，取开集可以保证给出一个开覆盖，使得二维映射整体是连续的）

于是 $\exists \set{s_j}$ 分划，使得 $F(N_{y_0}\times [s_j,s_{j+1}])\subseteq U_\alpha$，对于某 $\alpha$.

于是可以对 $j$ 做归纳法，$\exists !\tilde F:N_{y_0}\times I\to \tilde X$，使得 $p\circ \tilde F=F$，并且 $\tilde F|_{N_{y_0}\times \set{0}}=\tilde f|_{N_{y_0}}$.

$\forall y_1\in Y$，也有 $\exists !\tilde F:N_{y_1}\times I\to \tilde X$，使得 $p\circ \tilde F=F$，且 $\tilde F|_{N_{y_1}\times\set{0}}=\tilde f|_{N_{y_1}}$.

当 $N_{y_1}\cap N_{y_0}\neq \varnothing$，由道路提升的唯一性，我们也可以知道它们诱导出的提升在交集中是一致的。这就是说 $\forall y\in N_{y_0}\cap N_{y_1}$，两个 $\tilde F$ 在 $\set{y}\times [0,1]$ 是一致的。

因此 $\exists !\tilde F:Y\times I\to \tilde X$.
覆叠空间基本群跟底空间基本群的关系

令 $p:\tilde X\to X$ 是一个覆叠映射，$p(\tilde x_0)=x_0$，则 $p_\star:\pi_1(\tilde X,\tilde x_0)\to \pi_1(X,x_0)$ 是一个单射。令 $<\alpha>\in \pi_1(X,x_0)$，则 $<\alpha>\in p_\star(\pi_1(\tilde X,\tilde x_0))$ 当且仅当 $\alpha$ 提升后是环路。

证明：

选取 $\tilde f:I\to \tilde X$ 使得它是一个基本点为 $\tilde x_0$ 的环路，且 $p_\star(<\tilde f>)=e$.

令 $f=p\circ\tilde f$，则 $\exists F:I\times I\to X$，使得 $F(s,0)=f(s)$，$F(s,1)=x_0$，$\forall s\in I$.

并且 $F(0,t)=F(1,t)=x_0,\forall t\in I$.

根据同伦提升引理，$\exists !\tilde F:I\times I\to \tilde X$，使得 $p\circ \tilde F=F$，$\tilde F(s,0)=\tilde f(s)$.

注意到 $\tilde F(0,t)$ 与 $\tilde F(1,t)$ 是 $F(0,t)$ 以及 $F(1,t)$ 的提升，$F(0,t)=F(1,t)=x_0$.

由道路提升的唯一性，$\tilde F(0,t)=\tilde F(1,t)=\tilde x_0$.

观察 $\tilde F(s,1)$，它是 $F(s,1)=x_0$ 的提升，仍然根据道路提升的唯一性，有 $\tilde F(s,1)=\tilde x_0$.

于是，$\tilde f\underset{\tilde F}\simeq \text{constant loop at } x_0\text{ rel}\set{0,1}$. 于是 $<\tilde f>=e$.

于是 $p_\star$ 是单射。

如果 $\tilde f$ 是一个 $f$ 的提升且 $\tilde f$ 是一个环路，则 $p_\star<\tilde f>=<p\circ f>$，因此 $<f>\in p_\star(\pi_1(\tilde X,\tilde x_0))$.

如果 $<f>\in p_\star(\pi_1(\tilde X,\tilde x_0))$，则 $p\circ \tilde f\underset{F}\simeq f\text{ rel}\set{0,1}$. 对某一 $\tilde f$. 根据同伦提升引理，$\exists \tilde F:I\times I\to \tilde X$，使得 $p\circ\tilde F=F$，且 $\tilde F(0,t)=\tilde F(1,t)=\tilde x_0$. （道路提升的唯一性）

因此 $p\circ \tilde F(s,1)=f$，而 $\tilde F(s,1)$ 是在 $\tilde x_0$ 处的环路，从而得证。
覆叠映射是局部常数

考虑一个覆叠映射 $p:\tilde X\to X$，记 $|p^{-1}(X)|$ 表示集合 $p^{-1}(X)$ 的势 (Cardinality)，我们有 $p$ 在 $X$ 上是局部常数，这是说 $\forall x_0\in X$，$\exists U$ 是 $x_0$ 的邻域，使得 $|p^{-1}(x)|=|p^{-1}(x_0)|$，$\forall x\in U$ (令 $U$ 使得 $p^{-1}(U)=\bigsqcup_{\beta}V_\beta$，$p|_{V_\beta}:V_\beta\to U$ 同胚)。

如果我们假设底空间 $X$ 是连通的，则 $|p^{-1}(x)|$ 是一个整体常数 $\forall x\in X$，我们称 $|p^{-1}(x)|$ 为覆叠映射 $p$ 的层数 (Number of Sheets)。
覆叠映射的层数

令 $p:\tilde X\to X$ 是一个覆叠映射，假设 $X,\tilde X$ 是道路连通的。则 $p$ 的层数等于 $H=p_\star(\pi_1(\tilde X,\tilde x_0))$ 在 $\pi_1(X,x_0)$ 的指标 (Index). （指标就是在大群中陪集的个数）

证明：

考虑两个环路 $g,h$ 基本点为 $x_0$，$<h>\in H$.

令 $\tilde g$ 和 $\tilde h$ 是 $g,h$ 的提升。由于 $<h>\in H$，有 $\tilde h$ 是环路。我们有 $(\tilde h\cdot\tilde g)(1)=\tilde g(1)$。

令 $\varphi:\set{\text{陪集} H<g>\mid <g>\in \pi_1(X,x_0)}\to p^{-1}(x_0)$，其中 $\varphi(H<g>):=\tilde g(1)$. 这是良好定义的。

由于 $\tilde X$ 是道路连通的，$\forall x\in p^{-1}(x_0)$，$\exists \tilde g:I\to \tilde X$，有 $\tilde g(0)=\tilde x_0,\tilde g(1)=x$. 令 $g=p\circ \tilde g$，有 $\varphi(H<g>)=\tilde g(1)=x$，因此 $\varphi$ 是满射。

如果 $\varphi(H<g_1>)=\varphi(H<g_2>)$，则 $\tilde g_1(1)=\tilde g_2(1)$，有 $\tilde g_1\cdot\tilde g_2^{-1}$ 是一个 $\tilde x_0$ 处的环路，且它是 $g_1g_2^{-1}$ 的提升。这意味着 $<g_1><g_2>^{-1}\in H$，因此 $H<g_1>=H<g_2>$. 因此 $\varphi$ 是单射。
提升判别法 (Lifting Criterion)

给定一个覆叠映射 $p:(\tilde X,\tilde x_0)\to (X,x_0)$ （记号表示 $p(\tilde x_0)=x_0$），令 $Y$ 是一个道路连通且局部道路连通的空间。令 $f:(Y,y_0)\to (X,x_0)$ 连续映射，则 $\exists f$ 的提升 $\tilde f$ 当且仅当 $f_\star(\pi_1(Y,y_0))\subset p_\star(\pi_1(\tilde X,\tilde x_0))$.

形式上看，这是图上的交换图表。
- 局部道路连通 (Locally Path-Connected)
  称一个集合 $Y$ 是局部道路连通，若 $\forall y\in Y$ 以及 $\forall y$ 的邻域 $U$，$\exists$ 道路连通邻域 $V$ 使得 $y\in V,V\subseteq U$.
证明：

$(\Rightarrow):$ 这是平凡的。若 $\exists \tilde f$，则 $f=p\circ\tilde f$，这就是说 $f_\star=p_\star\circ \tilde f_\star$，于是 $f_\star(\pi_1(Y,y_0))\subseteq p_\star(\pi_1(\tilde X,\tilde x_0))$.

$(\Leftarrow):$ $\forall y\in Y$，选择一条道路 $\gamma:I\to Y$ 有 $\gamma(0)=y_0$，$\gamma(1)=y$。

此时有 $f\circ \gamma(0)=x_0$，于是 $\exists! \tilde{f\circ \gamma}$ 使得 $\tilde{f\circ\gamma}(0)=\tilde x_0$，我们定义 $\tilde f(y):=\tilde{f\circ\gamma}(1)$.

我们现在验证 $\tilde f$ 定义的合理性：

考察 $\gamma'$ 是另一条连接了 $y_0$ 与 $y$ 的道路，我们有 $h:=(f\circ \gamma')\cdot(f\circ\gamma)^{-1}$ 是一条在 $x_0$ 处的环路，并且 $<h>\in f_\star(\pi_1(Y,y_0))\subset p_\star(\pi_1(\tilde X,\tilde x_0))$.

因此 $h$ 的提升 $\tilde h$ 有 $\tilde h$ 是一条 $\tilde x_0$ 处的环路. 根据道路提升引理，有 $\tilde h(s/2)=\widetilde{f\circ\gamma'}(s)$, $\tilde h((s+1)/2)=\widetilde{(f\circ\gamma)}^{-1}(s)$, $\forall s\in I$.

因此 $h(1/2)=\widetilde{f\circ \gamma'}(1)=\widetilde{f\circ\gamma}(1)$，因此 $\tilde f$ 是良定义的。

令 $U$ 是一个 $f(y)$ 的邻域，令 $\tilde U$ 是 $\tilde f(y)$ 的邻域，使得 $p|_{\tilde U}$ 诱导了 $\tilde U$ 与 $U$ 的同胚。选取道路连通邻域 $V$ 是 $y$ 的邻域使得 $V\subset f^{-1}(U)$.

$\forall y'\in V$，选择道路 $\beta$ 连接 $y$ 与 $y'$，固定道路 $\gamma$ 从 $y_0$ 至 $y$.

我们复合道路，有 $(\widetilde {f\circ\gamma})(\widetilde {f\circ \beta})(1)=\tilde f(y')$，而 $\widetilde{f\circ\beta}=(p|_{\tilde U})^{-1}\circ f\circ\beta$，于是 $\tilde f(y')=(p|_{\tilde U})^{-1}\circ f(y')$，这是说 $\tilde f|_V=(p|_{\tilde U})^{-1}\circ f$，于是 $\tilde f$ 是连续映射。
提升的唯一性

令 $p:\tilde X\to X$ 是一个覆叠映射，令 $f:Y\to X$ 连续映射，$Y$ 是连通的。令 $\tilde f_1 \tilde f_2:Y\to\tilde X$ 是两个 $f$ 的提升且 $\exists y_0\in Y$，有 $\tilde f_1(y_0)=\tilde f_2(y_0)$，则 $\tilde f_1=\tilde f_2$.

证明：

令 $A=\set{y\in Y\mid \tilde f_1(y)=\tilde f_2(y)}$，令 $B=\set{y\in Y\mid \tilde f_1(y)\neq \tilde f_2(y)}$.

我们知道 $Y=A\sqcup B$ 且 $A\neq \varnothing$.

$\forall y\in A$，选取 $U$ 是一个 $y$ 的邻域，使得 $p^{-1}(U)=\bigsqcup_{\beta} V_\beta$ 且 $p|_{V_\beta}$ 是 $V_\beta$ 与 $U$ 的同胚。

根据 $\tilde f_1(y)=\tilde f_2(y)\in V_{\beta_0}$，$\exists y$ 的邻域 $N$ 使得 $\tilde f_1(N)\subset V_{\beta_0}$，$\tilde f_2(N)\subset V_{\beta_0}$. 由于 $p\circ \tilde f_1|_{N}=p\circ \tilde f_2|_N$，有 $\tilde f_1|_N=p^{-1}\circ f|_N=\tilde f_2|_N$，因此 $A$ 是开集。

对于 $y\in B$，则 $\tilde f_1(y)\in V_{\beta_1}$，$\tilde f_2(y)\in V_{\beta_2}$，则 $\exists y$ 的邻域 $N$ 使得 $\tilde f_1(N)\subset V_{\beta_1}$, $\tilde f_2(N)\subset V_{\beta_2}$，于是 $\tilde f_1|_N\neq \tilde f_2|_N$，于是 $B$ 是开集。

由于 $Y$ 是连通的，有 $A=Y,B=\varnothing$. 于是得出结论。

18. 万有覆叠空间

万有覆叠空间 (Universal Covering Space)

某种意义上“最大”的覆叠空间

万有覆叠空间 (Universal Covering Space)

考虑 $p:\tilde X\to X$ 是一个覆叠映射，若 $\pi_1(\tilde X)$ 是平凡群，则称 $\tilde X$ 是 $X$ 的一个万有覆叠空间（Universal Covering Space).
准备工作：局部道路连通 (Locally Path-Connected)

将空间 $X$ 称作是局部道路连通 (Locally Path-Connected)的，如果对 $\forall x\in X$ 与其任意的一个邻域 $U$，则 $\exists$ 一个道路连通邻域 $V\subseteq U$ 且 $x\in V$.

事实上，局部道路连通和道路连通是两个很不一样的概念。

考虑一个平面上分离的两个圆盘，这个空间自然是局部道路连通但不是道路连通的（因为圆盘本身是道路连通的）

再来看一个是道路连通但不是局部道路连通的例子：

考虑一组斜率为 $1,1/2,1/3,\cdots$ 的射线如下图：

该空间确实是道路连通的但不是局部道路连通的，这是因为任取一个水平线上的点 $x$（除了原点），取一个不包含原点的邻域，都有这个邻域不会有一个包含 $x$ 的道路连通的子邻域。
准备工作：半局部单连通 (Semilocally Simply-Connected)

我们称 $X$ 是半局部单连通 (Semilocally Simply-Connected)的，若任取 $x\in X$，$\exists$ 邻域 $U$，使得 $i_\star(\pi_1(U,x))=\set{e}$，其中 $i$ 是嵌入映射。
- 注：可以注意到这里的定义没有要求要从任意邻域 $U$ 中取出一个局部单连通的更小邻域 $V$。这是因为，如果我们仿照上面的做法去做，那么不妨考虑任意 $U$ 邻域中的小邻域 $V$，有先考虑 $V$ 到 $U$ 中的嵌入映射，再考虑 $U$ 到 $X$ 的嵌入映射，我们可以发现 $i_\star(\pi_1(V,x))=\set{e}$.
半局部单连通是万有覆叠空间的必要条件

令 $p:\tilde X\to X$ 万有覆叠映射，则 $X$ 是半局部单连通。

证明：

$\forall x\in X$，选取邻域 $U$，使得 $p^{-1}(U)=\bigsqcup_\beta V_\beta$，且 $p|_{V_\beta}$ 给出了 $V_\beta\to U$ 同胚；

验证 $U$ 符合定义：取出 $\gamma:I\to U$ 是一个 $x_0$ 处环路，我们可以将 $\gamma$ 提升到 $V_{\beta_0}$ 中，其基本点变为 $\tilde x_0$，提升后的环路为 $\tilde \gamma$，$\forall \beta_0$（尽管对任意 $\beta_0$ 成立，我们不妨取定某个 $\beta_0$）。

由于 $\pi_1(\tilde X)$ 是平凡的，$\exists \tilde F:I\times I\to \tilde X$ 使得 $\tilde \gamma\underset{\tilde F}\simeq C_{\tilde x_0}\text{ rel}\set{0,1}$，$C_{\tilde x_0}$ 是常数道路。从而，$\gamma\underset{p\circ\tilde F}\simeq C_{x_0}\text{ rel}\set{0,1}$，其中 $C_{x_0}$ 是 $x_0$ 处的常数道路。

因此 $i_\star(<\gamma>)=e$，因此 $X$ 是半局部单连通。
主定理：万有覆叠空间的构造

设 $X$ 是道路连通、局部道路连通、半局部单连通，则 $\exists$ 万有覆叠空间 $\tilde X$.

证明：

我们先给出整体的构造思路：

固定 $x_0\in X$，令 $\tilde X=\set{<\gamma>\mid \gamma:I\to X,\gamma(0)=x_0}$，其中 $<\gamma>$ 是 $\gamma$ 所在的同伦类（$\text{rel}\set{0,1}$）

令 $p:\tilde X\to X$，$p(<\gamma>):=\gamma(1)\in X$，我们希望装备一个拓扑结构，并证明 $p$ 是一个覆叠映射。由于 $X$ 是道路连通的，我们有 $p$ 是一个满射。

为了在 $\tilde X$ 上装备一个拓扑，我们考虑一个集族 $\beta=\set{U\subseteq X\text{ open}\mid U\text{ path-connected, }i_\star(\pi_1(U))=\set{e}\subseteq\pi_1(X)}$，$i$ 为嵌入映射.

首先，$\beta$ 是一个 $X$ 的拓扑基，这是因为：

由于 $X$ 是半局部单连通，$\beta$ 中的成员可以覆盖 $X$，即 $X=\bigcup_{U\in \beta} U$；

另外，$\forall U_1,U_2\in \beta$ 且 $U_1\cap U_2\neq\varnothing$，$\forall x\in U_1\cap U_2$，选择一个道路连通邻域 $V\subset U_1\cap U_2$（局部道路连通），考虑 $i_\star(\pi_1(V))$，上面我们已经说明过 $i_\star(\pi_1(V))=\set{e}\subseteq \pi_1(X)$.

于是我们推出，$V\in \beta$，于是 $\beta$ 符合拓扑基性质，是 $X$ 的一族拓扑基。

接着我们利用 $\beta$ 来为 $\tilde X$ 装备一个拓扑：

$\forall U\in \beta$，考虑 $\gamma$ 是一个道路使得道路的起点是 $x_0$，道路的终点 $\in U$.

我们定义 $U_{<\gamma>}:=\set{<\gamma\cdot\eta>\mid \eta:I\to U\text{ with } \eta(0)=\gamma(1)}$.

由于 $U$ 是道路连通的，因此 $p:U_{<\gamma>}\to U$ 是一个满射；

另一方面，任取 $\eta_1,\eta_2$ 是 $U$ 中道路，使得 $\eta_1(0)=\eta_2(0)=\gamma(1)$，$\eta_1(1)=\eta_2(1)$.

我们会发现，$<\eta_1\eta_2^{-1}>=e\in\pi_1(X)$，因此 $\eta_1\simeq \eta_2\text{ rel}\set{0,1}$，于是 $<\gamma\cdot \eta_1>=<\gamma\cdot\eta_2>$.

因此 $p:U_{<\gamma>}\to U$ 是单射。

另外，令 $<\gamma'>\in U_{<\gamma>}$，则 $\gamma'=\gamma\cdot \eta$ 对某个 $\eta:I\to U$ 且 $\eta(0)=\gamma(1)$.

考虑 $U_{<\gamma'>}$ 任意的元素，其形如 $<\gamma\cdot \eta\cdot\alpha>$，$\alpha:I\to U$，因此 $U_{<\gamma'>}\subseteq U_{<\gamma>}$；反过来，任意 $U_{<\gamma>}$ 中的元素都形如 $<\gamma\cdot\beta>$，可以被写成 $<\gamma\cdot\eta\cdot\eta^{-1}\cdot\beta>=<\gamma'\cdot\eta^{-1}\cdot\beta>$，于是 $U_{<\gamma>}\subseteq U_{<\gamma'>}$，因此：

$U_{<\gamma>}=U_{<\gamma'>}\ \ \ (\star)$.

令 $\tilde \beta=\set{U_{<\gamma>}\mid U\in \beta,\gamma(0)=x_0,\gamma(1)\in U}$. 我们来验证 $\tilde \beta$ 是一个拓扑基：

首先，$\tilde X=\bigcup_{U_{<\gamma>}\in \tilde\beta} U_{<\gamma>}$，这是易于验证的；

其次，任取 $U_{<\gamma>},V_{<\gamma'>}\in \tilde\beta$ 与 $\forall <\gamma''>\in U_{<\gamma>}\cap V_{<\gamma'>}$.

根据上面的 $(\star)$，我们有 $U_{<\gamma''>}=U_{<\gamma>},V_{<\gamma''>}=V_{<\gamma>}$.

我们选取 $W\in \beta$ 使得 $W\subseteq U\cap V$，且 $\gamma''(1)\in W$（$\beta$ 是拓扑基）

则 $W_{<\gamma''>}\subset U_{<\gamma''>}\cap V_{<\gamma''>}$，且 $<\gamma''>\in W_{<\gamma''>}$.

因此，$\tilde \beta$ 是一个拓扑基；于是我们为 $\tilde X$ 装备上一个拓扑，使得该拓扑的拓扑基是 $\tilde\beta$.

接下来我们验证我们刚才构造的双射 $p:U_{<\gamma>}\to U$ 确实是一个同胚：

这是因为，$\forall V_{<\gamma'>}\subseteq U_{<\gamma>}$，$p(V_{<\gamma'>})=V\in \beta$；反过来，$\forall V\subseteq U, V\in \beta$，则 $p^{-1}(V)\cap U_{<\gamma>}=V_{<\gamma'>}$，其中 $<\gamma'>\in U_{<\gamma>},\gamma'(1)\in V$.

特别地，我们考虑 $p:\tilde X\to X$，它是一个连续映射（局部同胚）。

如果 $U_{<\gamma>}\neq U_{<\gamma'>}$，其中 $U\in \beta$，则我们知道 $U_{<\gamma>}\cap U_{<\gamma'>}=\varnothing$. （如果 $\exists <\gamma''>\in U_{<\gamma>}\cap U_{<\gamma'>}$，根据 $(\star)$ 就有 $U_{<\gamma>}=U_{<\gamma''>}=U_{<\gamma'>}$）

因此，$p^{-1}(U)$ 长成一些形如 $U_{<\gamma>}$ 的不交并。因此 $p$ 是一个覆叠映射。

最后，我们来验证 $\tilde X$ 是单连通的：

令 $<\gamma>\in \tilde X$，令 $\gamma_t(s)=\gamma(ts),s\in I$.

定义一种对于道路 $\gamma$ 的变换 $\varphi:I\to\tilde X$，其中 $\varphi(t)=<\gamma_t>$. （形式上讲，这就是把 $\gamma$ “画” 出来）

其中 $\varphi(0)$ 是常数道路 $<C_{x_0}>$，$\varphi(1)=<\gamma>$.

于是 $\tilde X$ 是道路连通的。

由于 $p_\star$ 是单射，我们只需要验证 $p_\star(\pi_1(\tilde X,<C_{x_0}>))=\set{e}$.

令 $\gamma$ 是一个基本点为 $x_0$ 的环路，且 $<\gamma>\in p_\star(\pi_1(\tilde X,<C_{x_0}>))$，则 $\gamma$ 可以被提升为 $\tilde X$ 中的环路，且环路的基本点为 $<C_{x_0}>$.

对 $\gamma$ 应用变换，$\varphi(t)=<\gamma_t>$，则 $p\circ \varphi=\gamma$. 因此 $\varphi$ 确实是 $\gamma$ 的一个提升。

刚才我们提到， $\gamma$ 提升后是一个环路。

由于 $\varphi(0)=<C_{x_0}>$，由道路提升的唯一性，$\varphi$ 也是一个环路，但 $\varphi(1)=<\gamma>=\varphi(0)$，从而 $<\gamma>=e$.
定理：任意子群覆叠空间的构造

令 $X$ 是道路连通，局部道路连通，半局部单连通，则 $\forall$ 子群 $H\subset \pi_1(X,x_0)$，$\exists$ 覆叠空间及覆叠映射 $p:X_H\to X$，使得 $p_\star(\pi_1(X_H,\tilde x_0))=H$，其中 $\tilde x_0\in p^{-1}(x_0)$.

证明：

令 $\tilde X$ 是 $X$ 的万有覆叠空间。沿用上面定理的记号，我们如下构造粘合空间：

令 $\forall <\gamma>,<\gamma'>\in \tilde X$，定义一个等价关系 " $\sim$ "， $<\gamma>\sim <\gamma'>$ 当且仅当 $\gamma(1)=\gamma'(1)$ 且 $<\gamma\cdot(\gamma')^{-1}>\in H$.

由于 $H$ 是一个群，因此我们给出的关系确实是一个等价关系。

令 $X_H$ 是一个 $\tilde X$ 由等价关系给出的粘合空间，$<\gamma>$ 与 $<\gamma'>$ 被粘合当且仅当 $<\gamma>\sim<\gamma'>$.

$\exists p:X_H\to X$，$p(<\gamma>)=\gamma(1)$.

令 $\gamma(1)=\gamma'(1)$ 并且 $<\gamma> \sim <\gamma'>$，选取 $U\in \beta\text{ s.t. }\gamma(1)\in U$，从而 $\forall \eta:I\in U,\eta(0)=\gamma(1)$，我们有 $<\gamma\eta>\sim<\gamma'\eta>$.

此时，$U_{<\gamma>}$ 以及 $U_{<\gamma'>}$ 被粘合在了一起。

于是关于 $p$ 对每个 $U$ 取逆，拉回 $X_H$ 后仍然可以写成若干与 $U$ 同胚开集的不交并，于是 $p:X_H\to X$ 是一个覆叠映射。

令 $\tilde x_0\in X_H$ 是常数道路 $<C_{x_0}>$ 的等价类。

令 $\gamma$ 是一个 $x_0$ 处的环路，$\phi:I\to \tilde X$，$\phi(t)=<\gamma_t>$.

根据上一个定理的证明，我们可以说明 $\phi$ 是 $\gamma$ 的提升。

如果我们在 $X_H$ 看 $\phi$ 的像，$\phi$ 是一个环路当且仅当 $\phi(1)=<\gamma>\sim\phi(0)=<C_{x_0}>$.

这就是说 $<\gamma>\in H$.

于是 $p_\star(\pi_1(X_H,\tilde x_0))=H$.
- 注：覆叠空间间的粘合映射还是覆叠映射
  
  事实上，我们在这两个定理证明里出现的三个映射都是覆叠映射。这是因为，我们考察粘合映射开集的原像，它是 $\tilde X$ 中一些开集的不交并。
  
  更多地，若 $H_1\subset H_2$，则我们可以类似得到另一张图，且这些映射全都是覆叠映射：
定义：覆叠映射(空间)的同构 (Isomorphism of Covering Maps/Spaces)

令 $p_1:\tilde X_1\to X$，$p_2:\tilde X_2\to X$ 是两个覆叠映射，称 $p_1,p_2$ 是同构的，若 $\exists$ 同胚 $f:\tilde X_1\to\tilde X_2$，使得 $p_1=p_2\circ f$.

这就是在说下面的交换图表：

（即，在同胚的基础上，诱导了一个交换图表）
同构是一个等价关系

这是易于验证的。

19. 覆叠空间的分类与甲板变换

覆叠空间的分类定理

定义：覆叠空间的同构

令 $p_1:\tilde X_1\to X$，$p_2:\tilde X_2\to X$ 是两个覆叠映射，称 $p_1,p_2$ 是同构的，若 $\exists$ 同胚 $f:\tilde X_1\to\tilde X_2$，使得 $p_1=p_2\circ f$.
唯一性定理

令 $X$ 是道路连通、局部道路连通，则如果有两个道路连通的覆叠空间 $p_1:\tilde X_1\to X, p_2:\tilde X_2\to X$，则 $p_1$ 与 $p_2$ 是同构且同构对应的同胚映射 $f:\tilde X_1\to \tilde X_2$ 满足有 $f(\tilde x_1)=\tilde x_2$ （其中 $\tilde x_1\in p_1^{-1}(x_0)$, $\tilde x_2\in p_2^{-1}(x_0)$），当且仅当 $p_{1_\star}(\pi_1(\tilde X_1,\tilde x_1))=p_{2_\star}(\pi_1(\tilde X_2,\tilde x_2))$.

证明：

$(\Rightarrow):$ 如果 $\exists$ 同构 $f$，则 $p_1=p_2\circ f,p_2=p_1\circ f^{-1}$. 于是 $p_{1_\star}=(p_{2_\star}\circ f_\star), p_{2_\star}=(p_{1_\star}\circ f^{-1}_\star)$.

由此 $p_{1_\star}(\pi_1(\tilde X_1,\tilde x_1))=p_{2_\star}(\pi_1(\tilde X_2,\tilde x_2))$.

$(\Leftarrow):$ 如果 $p_{1_\star}(\pi_1(\tilde X_1,\tilde x_1))=p_{2_\star}(\pi_1(\tilde X_2,\tilde x_2))$，由提升判别法，$\exists$ 提升 $\tilde p_1:\tilde X_1\to \tilde X_2$，使得 $p_2\circ \tilde p_1=p_1$. 同理也存在着提升 $\tilde p_2:\tilde X_2\to\tilde X_1$，使得 $p_1\circ \tilde p_2=p_2$.

这就是下图的交换图表：

如果我们将图表的起点换成 $\tilde X_2$：

根据第一张图表，$\tilde p_2\circ\tilde p_1$ 是一个 $p_1$ 的提升；根据第二张图表，$\tilde p_1\circ\tilde p_2$ 是一个 $p_2$ 的提升。

由提升的唯一性，有 $\tilde p_2\circ\tilde p_1=\text{id} \tilde X_1$，$\tilde p_1\circ\tilde p_2=\text{id} \tilde X_2$，因此 $\tilde p_1$ 与 $\tilde p_2$ 是互逆的同构。
覆叠空间的分类定理 (Classification of Covering Spaces)

令 $X$ 是道路连通、局部道路连通、半局部单连通，则有如下的分类定理：
- $\exists$ 从所有保持基本点的（道路连通）覆叠空间同构类 $p:(\tilde X,\tilde x_0)\to (X,x_0)$ 到底空间 $X$ 基本群 $\pi_1(X,x_0)$ 中所有子群构成的集合的双射，该双射将 $(p:(\tilde X_0,\tilde x_0)\to (X,x_0))$ 映射到 $p_\star(\pi_1(\tilde X,\tilde x_0))$.
- 如果我们将基本点忽略掉（即，对两个覆叠空间，如果我们能取出同胚映射 $f$，使得这两个覆叠空间存在两个覆叠映射 $p_1,p_2$，有 $p_1=f\circ p_2$，我们就将覆叠空间视为相同的），我们还可以得到另一个双射，从（道路连通）覆叠空间的同构类构成的集合 $p:\tilde X\to X$ 到底空间 $X$ 基本群 $\pi_1(X,x_0)$ 子群的共轭类构成的集合。
证明：

对第一条，上一节课中我们已经证明了它是一个满射（万有覆叠空间构造任意子群的覆叠空间）。刚才我们证明了它是单射。

下面我们来证明第二条：

如果 $p:\tilde X\to X$ 是一个覆叠映射及 $\tilde x_0,\tilde x_1\in p^{-1}(x_0)$.

考虑一条道路 $\tilde \gamma:I\to \tilde X$ 使得 $\tilde \gamma(0)=\tilde x_0,\tilde\gamma(1)=\tilde x_1$.

令 $\gamma=p\circ\tilde \gamma$，这在底空间中是一个环路。

令 $g=<\gamma>\in \pi_1(X,x_0)$.

令 $H_i=p_\star(\pi_1(\tilde X,\tilde x_i)), i=0,1$.

任取一个 $\tilde \alpha: I\to\tilde X$，它是一个基本点为 $\tilde x_0$ 的环路。则 $\tilde\gamma^{-1}\cdot\tilde\alpha\cdot\gamma$ 是一个基本点为 $\tilde x_1$ 的环路。

我们将这个环路投影到底空间，即有 $g^{-1} H_0 g\subset H_1$.

同理，我们也有 $g H_1g^{-1}\subset H_0$，这就是说 $g^{-1} H_0 g=H_1$，$H_0$ 与 $H_1$ 共轭。

反过来，若我们先取定 $H_0=p_\star(\pi_1(\tilde X,\tilde x_0))$ 以及 $H_1=g^{-1} H_0 g$. 我们将刚才证明的步骤反过来，令 $g=<\gamma>$，其中 $\gamma$ 是一条环路。令 $\tilde \gamma$ 是 $\gamma$ 的提升，$\tilde \gamma(0)=\tilde x_0$，令 $\tilde x_1=\tilde\gamma(1)$.

由上述的计算过程，我们有 $p_\star(\pi_1(\tilde X,\tilde x_1))=H_1$.

甲板变换 (Deck Transformation)

定义：甲板变换 (Deck Transformation)

考虑一个覆叠空间 $p:\tilde X\to X$，其中 $p$ 为覆叠映射。考虑一个自同构 $f:\tilde X\to \tilde X$，我们将其称之为 甲板变换 (Deck Transformation)，所有的甲板变换形成一个群，群乘法为同构的复合。记这个群为 $G(\tilde X)$.

定义群作用 $G(\tilde X)\curvearrowright \tilde X$，其中 $f\cdot\tilde x:=f(\tilde x), f\in G(\tilde X),\tilde x\in\tilde X$.

假设 $\tilde X$ 是道路连通的，那么这个群作用是自由群作用 (free)，这就是说 $f\cdot\tilde x=\tilde x$ 当且仅当 $f=\text{id}_\tilde X$. （由提升的唯一性，将 $f$ 视作 $p$ 的提升）

此外，若 $\tilde x\in p^{-1}(x_0)$，则 $f \cdot\tilde x\in p^{-1}(x_0),\forall f\in G(\tilde X)$. （这就是说这个群作用是作用在每一个 $p^{-1}(x)$ 上的，即 $G(\tilde X)\curvearrowright p^{-1}(x)$）
- 正规覆叠空间 (Normal/Regular Covering Space)
  
  我们称 $p:\tilde X\to X$ 是一个正则覆叠空间，若 $G(\tilde X)$ 作用在每一个 $p^{-1}(x)$ 上都是传递的。
  
  这就是说 $\forall x\in X$，$\forall \tilde x,\tilde x'\in p^{-1}(x)$，$\exists f\in G(\tilde X)$，有 $f\cdot\tilde x=\tilde x'$.
正规覆叠空间相关定理

对正规覆叠空间，我们有两个定理：
1. 令 $X$ 是道路连通、局部道路连通，令 $p:(\tilde X,\tilde x_0)\to (X,x_0)$ 道路连通覆叠空间，令 $H=p_\star(\pi_1(\tilde X,\tilde x_0))\subset \pi_1(X,x_0)$，$\tilde X$ 是一个正规覆叠空间当且仅当 $H$ 是一个正规子群。
2. 令 $N(H)$ 是 $H$ 在 $\pi_1(X,x_0)$ 的正规化子（最大的使得 $H$ 是正规子群的子群），则考虑 $G(\tilde X)$，它同构于商群 $N(H)/H$，特别地，若 $p:\tilde X\to X$ 是正规的覆叠空间，则 $G(\tilde X)\cong \pi_1(X,x_0)/H$. 如果 $p:\tilde X\to X$ 是万有覆叠空间，则 $G(\tilde X)\cong \pi_1(X,x_0)$.
证明：
$\forall \gamma\in \pi_1(X,x_0)$，令 $\tilde \gamma$ 是 $\gamma$ 的提升，$\tilde\gamma(0)=\tilde x_0$. 令 $\tilde x_1=\tilde\gamma(1)$.

由之前的定理，$<\gamma>^{-1}p_\star(\pi_1(\tilde X,\tilde x_0))<\gamma>=p_\star(\pi_1(\tilde X,\tilde x_1))$.

因此 $\gamma\in N(H)$ 当且仅当 $p_\star(\pi_1(\tilde X,\tilde x_0))=p_\star(\pi_1(\tilde X,\tilde x_1))$.

这当且仅当 $\exists$ $f\in G(\tilde X)$ 使得 $\tilde x_1=f(\tilde x_0)$.

因此若 $p:\tilde X\to X$ 是一个正规覆叠空间当且仅当 $H$ 是一个正规子群。
令 $\varphi:N(H)\to G(\tilde X)$，$\varphi(<\gamma>)=f$ 使得 $f(\tilde x_0)=\tilde x_1$.

$\varphi(<\gamma>\cdot <\gamma'>)(\tilde x_0)$ 由定义是 $\widetilde{\gamma\cdot\gamma'}(1)$.

由于 $\widetilde {\gamma\cdot\gamma'}=\tilde \gamma\cdot f(\tilde\gamma')$ （可以借助下图辅助理解）

因此 $\widetilde {\gamma\cdot\gamma'}(1)=f\circ f'(\tilde x_0)$，其中 $\varphi(<\gamma'>)=f'$.

因此 $\varphi$ 确实是一个群同态。

我们来验证 $\varphi$ 是一个满射：$\forall f\in G(\tilde X)$，若 $f(\tilde x_0)=\tilde x_1$，令 $\tilde\gamma$ 是一条道路，起点为 $\tilde x_0$，终点是 $\tilde x_1$.

令 $\gamma =p\circ\tilde\gamma$. 由刚才的构造方式，$\varphi(<\gamma>)=f$. 因此 $\varphi$ 是一个满射。

若 $\varphi(<\gamma>)=\text{id}_\tilde X$，这等价于 $\tilde\gamma(1)=\tilde\gamma(0)=\tilde x_0$. 这等价于 $<\gamma>\in H$.

因此 $\ker \varphi= H$，于是 $N(H)/H\cong G(\tilde X)$.
由群作用构造覆叠空间

令 $G$ 是一个拓扑群，作用在某一个拓扑空间 $Y$ 上面。考虑下面的离散性质，记作 $(\star)$：

$\forall y\in Y$，$\exists$ 邻域 $U\subset Y$，使得 $\forall g_1\neq g_2\in G$，都有 $g_1(U)\cap g_2(U)=\varnothing$.
- 观察：离散性质是必要条件
  
  群作用 $G(\tilde X)\curvearrowright \tilde X$ 满足 $(\star)$.
  
  证明：
  
  $\forall \tilde x\in \tilde X$，根据覆叠空间定义，我们可以选取一个邻域 $\tilde x\in \tilde U$，使得 $p|_{\tilde U}:\tilde U\to U\subset X$ 同胚.
  
  假设 $\exists g_1\neq g_2\in G(\tilde X)$ 使得 $g_1(\tilde U)\cap g_2(\tilde U)\neq\varnothing$.
  
  这就是说 $\exists \tilde x_1,\tilde x_2\in \tilde U$，使得 $g_1(\tilde x_1)=g_2(\tilde x_2)$.
  
  因此 $\tilde x_1=g_1^{-1}\cdot g_2(\tilde x_2)$. 因此 $\tilde x_1,\tilde x_2$ 落在某一个 $p^{-1}(x)$ 上对于某个 $x\in U$.
  
  由于 $p^{-1}(x)\cap \tilde U$ 是一个单点，因此 $\tilde x_1=\tilde x_2$，因此 $g_1^{-1}g_2(\tilde x_1)=\tilde x_1$，因此 $g_1^{-1}g_2=\text{id}_\tilde X$，这与 $g_1\neq g_2$ 矛盾。
  
  这证明了必要条件。
定理：考虑群作用 $G\curvearrowright Y$ 使得作用满足 $(\star)$，则：
1. 考虑商映射 $p:Y\to Y/G$，这个映射是一个正规的覆叠映射；
2. 如果 $Y$ 是道路连通的，$G$ 是由甲板映射 (deck transformation) 构成的群；
3. 如果 $Y$ 是道路连通，局部道路连通的，则有 $G\cong \pi_1(Y/G)/p_\star(\pi_1(Y))$.
- 注：第三个定理的应用
  如果 $Y$ 是一个万有覆叠空间，那么我们可以用第三条计算复杂底空间的基本群。

20. 覆叠空间的构造与同调理论

覆叠空间的构造

回忆

$G\curvearrowright Y$，离散性质 $(\star)$ 说的是：$\forall y\in Y$，$\exists U\subset Y$ 使得 $U$ 是 $y$ 邻域，有 $\forall g_1\neq g_2\in G$，均有 $g_1(U)\cap g_2(U)=\varnothing$.

如果满足离散性质，我们会有如下定理：
1. 商映射 $p:Y\to Y/G$ 是一个正规的覆叠映射（正规：对于每一个 $p^{-1}(x)$ 是传递的）；
2. 如果 $Y$ 是道路连通的，则 $G$ 是由甲板映射 (Deck Transformation)构成的群；
3. 如果 $Y$ 是道路连通且局部道路连通的，则 $G\cong \pi_1(Y/G)/p_\star(\pi_1(Y))$.
定理的证明

证明：
$\forall y\in Y/G$，选择 $\tilde y\in Y$ 使得 $p(\tilde y)=y$.

选择一个邻域 $\tilde y\in U$ 使得其满足 $(\star)$.

这意味着 $p^{-1}(p(U))=\bigsqcup_{g\in G}g(U)$，并且 $p|_{g(U)}:g(U)\to p(U)$ 的同胚，我们来证明这一点：

由粘合拓扑的定义，$p|_{U}$ 是一个 $U\to p(U)$ 双射且连续（单射是因为 $U$ 满足 $(\star)$）；

$\forall V\subseteq U$，$p^{-1}(p(V))=\bigsqcup_{g\in G}g(V)$，由于 $V$ 是开集，有 $g(V)$ 也是开集，因此 $p^{-1}(p(V))$ 是开集，因此 $p(V)$ 是开集（粘合拓扑定义），因此 $p|_{U}$ 是一个同胚；

对于 $p|_{g(U)}=p\circ g|_{U}$，由于 $g$ 是同胚，因此这个映射仍然是同胚。

从而 $p$ 是一个覆叠映射。

我们验证正规性：$\forall g\in G$，它的群作用一定是甲板映射，从而由于 $g_2g_1^{-1}(g_1(U))=g_2(U)$，$\forall g_1,g_2\in G$，因此 $p$ 是一个正规的覆叠映射。
$G\subseteq G(Y)$ 这是因为 $\forall g\in G$ 都是甲板映射；

反过来，如果 $Y$ 是道路连通的，$\forall f\in G(Y)$，$\forall y\in Y$，$p(y)=p(f(y))$.

这意味着 $y,f(y)$ 落在了同一个轨道中，这意味着 $\exists g\in G$，使得 $g(y)=f(y)$.

这就是说 $f^{-1}\circ g(y)=y$. 这就是说 $f^{-1}\circ g=id_Y$. 因此 $g=f$.

从而 $G=G(Y)$.
由 (2) 与之前的定理：

可以直接推出第三问。
- 注：非正规覆叠映射基本群的商群
  
  对如下的图表，我们仍然可以用甲板映射构造出一个群作用构成的群。
  
  然而，此时 $\pi_1(X)/G(X_H)$ 不再 $\cong \pi_1(X_H)$，反而是 $\cong \pi_1(X_{N(H)})$.
例：环面的基本群

令 $G=\mathbb{Z}\times\mathbb{Z}$，令 $Y=\mathbb{R}^2$，我们定义 $G\curvearrowright Y$ 有 $(m,n)\cdot(x,y):=(x+m,y+n)$.

此前我们说明了这给出了 $\mathbb{R}^2$ 的一个“格点“。

我们以前也说明过，$Y/G$ 同胚于环面，并且我们可以验证该作用 $(\star)$。

由于 $\pi_1(Y)$ 是平凡群，有 $\pi_1(Y/G)\cong G=\mathbb{Z}\times\mathbb{Z}$.
例：实射影空间的基本群

令 $G=\mathbb{Z}_2=\set{-1,1}$，$Y=S^n$. 定义群作用 $G\curvearrowright Y$，$-1\cdot x:=-x$.

我们此前证明过 $Y/G\cong\mathbb{R}P^n$，且这个群作用确实满足 $(\star)$.

由于 $\pi_1(S^n)=\set{e}$，从而 $\pi_1(\mathbb{R}P^n)\cong G=\mathbb{Z}_2$，$\forall n\geq 2$.

同调理论 (Homology Theorem)

引入

我们此前说明过，

从某种意义上讲，可以说 $\pi_1$ 这个指标”探测“到了这个集合与 $\mathbb{R}^2$ 的区别，因为 $\pi_1(\mathbb{R}^2\setminus\set{0})=\mathbb{Z}\neq\set{e}$.

但是 $\pi_1$ 指标并不是万能的。对于三维空间，有 $\pi_1(\mathbb{R}^3\setminus\set{0})=\pi_1(S^2)=\set{e}$，这无法再被 $\pi_1$ 探测到。

因此，我们需要一些高维的拓扑不变量来解决这个问题。

一个曾经说过的例子是 $\pi_n(X)$，这就是考虑所有 $S^n\to X$ 的映射，这被称之为高维同伦群（由于 $n\geq 2$ 时，这个群变得很难以计算，因此我们课程不会研究它）；

此外，我们还可以研究 $H_n(X)$，这就是我们即将要介绍的同调群 (Homology Group).

我们会在课程中涉及三个版本的同调理论，这从三个角度看待了同一问题：

它们分别是单纯同调论 (Simplicial Homology)，奇异同调论 (Singular Homology)，胞腔同调论(Celluar Homology)，我们以后会说明这三者事实上是同构的。
单形 (Simplex)

固定 $v_0,\cdots,v_n\in\mathbb{R}^m$，假设 $v_1-v_0,v_2-v_0,\cdots,v_n-v_0$ 是线性无关的，这等价于 $v_0,\cdots,v_n$ 不落在某个 $n-1$ 维的超平面里。

我们令 $[v_0,\cdots,v_n]$ 表示下面这些点的集合：$\set{\lambda_0v_0+\cdots+\lambda_nv_n\mid \sum \lambda_i=1,\lambda_i\geq 0}$ （这就是 $v_0,\cdots,v_n$ 的凸包，即为包含了 $\set{v_0,\cdots,v_n}$ 的最小凸集）。

我们将 $[v_0,\cdots,v_n]$ 称为 $n$ 维单形，或 $n$-单形 ($n$-Simplex)，这事实上也给出了顶点的顺序：$v_0,\cdots,v_n$.
- $0$ 维单形
  
  单点 $[v_0]$；
- $1$ 维单形
  
  线段 $[v_0,v_1]$；
- $2$ 维单形
  
  三角形 $[v_0,v_1,v_2]$；
- $3$ 维单形
  
  四面体 $[v_0,v_1,v_2,v_3]$；
- $n$ 维单形
  
  事实上就是四面体的推广，情形类似。
标准 $n$ 维单形 (Standard $n$-Simplex)

令 $\Delta^n=\set{(t_0,\cdots,t_n)\in \mathbb{R}^{n+1}\mid t_0+\cdots+t_n=1,t_i\geq 0}$，我们称它是标准 $n$ 维单形 (Standard $n$-Simplex)。

例如，下图为标准一维单形：
典范线性同胚与重心坐标 (Canonical Linear Homeomorphism & Barycentric Coordinates)

令 $[v_0,\cdots,v_n]$ 是一个 $n$ 维单形，我们有一个 典范线性同胚 (Canonical Linear Homeomophism)，其中 $h:\Delta^n\to [v_0,\cdots, v_n]$，有 $h(t_0,\cdots,t_n)=\sum_{i=0}^n t_iv_i$.

我们将系数 $(t_0,\cdots,t_n)$ 称为点 $\sum_i t_iv_i$ 的重心坐标 (Barycentric Coordinates)。
面 (Face)

称单形 $[v_0,\cdots,v_n]$ 的一个面 (Face)为一个子单形，使得这个单形的顶点集合是 $\set{v_0,\cdots,v_n}$ 的非空子集。

面的顶点顺序由大单形 $[v_0,\cdots,v_n]$ 的顶点顺序诱导。

例如，对于一个三维单形 $[v_0,v_1,v_2,v_3]$，它的面既可以是二维的面如 $[v_0,v_1,v_3]$，也可以是一维的棱 $[v_1,v_3]$，还可以是顶点如 $[v_0]$. 不管如何，其顶点序都如图所示被三维大单形诱导。
奇异同调群 (Simgular Homology)

令 $X$ 是一个拓扑空间，一个奇异 $n$-单形 (Singular $n$-Simplex)是一个连续映射 $\sigma:\Delta^n\to X$。

令 $C_n(X)$ 是一个自由 Abel 群，它的一组基是所有 $X$ 中的奇异 $n$-单形。这就是说 $C_n(X)$ 中的元素形如形式和：$\sum_{i}n_i\sigma_i$，其中 $n_i\in \mathbb{Z}$，$\sigma_i:\Delta^n\to X$ 奇异 $n$-单形，且求和只有有限多个 $n_i$.

我们将 $C_n(X)$ 中元素称作是 $n$-链 ($n$-Chains)。

定义 $\sigma:\Delta^n\to X$ 的取边界操作 $\partial_n(\sigma)=\sum_{i=0}^n(-1)^i\sigma|_{[v_0,\cdots,\hat v_i,\cdots,v_n]}$，其中 $\Delta^n=[v_0,\cdots,v_n]$，$\hat v_i$ 表示将 $v_i$ 删去，即 $[v_0,\cdots,\hat v_i,\cdots,v_n]=[v_0,\cdot,v_{i-1},v_{i+1},\cdots,v_n]$.

我们将 $\partial_n$ 线性延拓到 $C_n$ 中，就可以得到一个群同态 $\partial_n:C_n(X)\to C_{n-1}(X)$，将其称之为取边界映射 (Boundary Map).
- 引理：取边界映射复合为 $0$
  
  取边界映射的复合映射 $C_n(x)\xrightarrow{\partial_n}C_{n-1}(x)\xrightarrow{\partial_{n-1}}C_{n-2}(x)$ 是零。
  
  证明：
  
  $\partial_{n-1}\partial_n(\sigma)=\partial_{n-1}(\sum_{i=0}^{n}(-1)^i\sigma|_{[v_0,\cdots,\hat v_i,\cdots,v_n]})$.
  
  进一步展开，有 $\sum_{j<i}(-1)^i(-1)^j\sigma|_{[v_0,\cdots,\hat v_j,\cdots,\hat v_i,\cdots,v_n]}+\sum_{j>i}(-1)^i(-1)^{j-1}\sigma|_{[v_0,\cdots,\hat v_i,\cdots,\hat v_j,\cdots,v_n]}$.
  
  注意求和项两两抵消（前半部分的系数与后半部分相反），因此整个式子为 $0$.
这告诉我们 $\ker \partial_n\supseteq \text{Im} \partial_{n+1}$.
- 定义：奇异同调群
  
  考虑商群 $\ker \partial_n/\text{Im} \partial_{n+1}$，我们将这个商群称为空间 $X$ 的 $n$ 维奇异同调群 (Singular Homology Group)，记作 $H_n(X)$.
- 圈，边界元与同调
  
  我们将 $\ker \partial_n$ 中的元素称之为圈 (Cycles)，与之前说到的链相对；
  
  我们将 $\text{Im} \partial_{n+1}$ 中的元素称之为边界元 (Boundaries)。
  
  我们将两个圈 $a,b$ 称作同调 (Homologous)的，如果 $a-b\in \text{Im} \partial_{n+1}$.
- 链复形 (Chain Complex)
  
  一般情况下，如果我们有 Abel 群群同态的序列 $\cdots\rightarrow C_{n+1}\xrightarrow{\partial_{n+1}}C_n\xrightarrow{\partial_n}C_{n-1}\rightarrow\cdots$ 使得任意两个相邻的 $\partial_{n+1}$ 与 $\partial_n$，有 $\partial_n\circ\partial_{n+1}=n$，则我们将这个序列称作一个链复形 (Chain Complex)，且可以定义商群 $H_n=\ker \partial_n/\text{Im} \partial_{n+1}$，将这个商群称之为链复形的 $n$ 维同调群。
  
  这事实上属于同调代数 (Homology Algebra)相关内容（研究链复形的一个数学分支）。
定理：单点的同调群

$H_n(\text{point})=\begin{cases}\mathbb{Z}&n=0\\0&n>0\end{cases}$.

证明：

记这个单点为 $p$，$\forall \Delta_n$，$\exists!\sigma_i:\Delta_n\to p$，因此 $\forall C_n(x)=\mathbb{Z}$.

我们知道 $\partial_n \sigma_n=\sum_{i=0}^n (-1)^i \sigma_{n-1}=\begin{cases}0&n\text{ odd}\\\sigma_{n-1}&n\text{ even}\end{cases}$

于是 $\cdots\to C_{n+1}\xrightarrow{\partial_{n+1}}C_n\xrightarrow{\partial_n}C_{n-1}\to\cdots$ 形如 $\cdots\to\mathbb{Z}\xrightarrow{\sim}\mathbb{Z}\xrightarrow{0}\mathbb{Z}\xrightarrow{\sim}\cdots\xrightarrow{0} \mathbb{Z}(=C_0(X))\to 0$

这就是说，$\ker\partial_n=\text{Im} \partial_{n+1}$，$\forall n\geq 1$，因此 $H_n(\text{point})=0,n>0$.

21. 同调群

同调理论 (Homology Theorem)

回忆：奇异同调群 (Singular Homology)

同调群 $H_n = \text{ker} \partial_n / \text{Im} \partial_{n + 1}$，其中 $\cdots \to C_{n + 1}(X) \xrightarrow{\partial_{n + 1}} C_n(X) \xrightarrow{\partial_{n}} C_{n - 1}(X) \to \cdots$

有时候我们也将 $\ker \partial_n$ 和 $\text{Im} \partial_{n + 1}$ 分别记作 $Z_n(x)$ 和 $B_n(x)$

对于单点的同调群，有 $H_n(\text{point}) = \begin{cases} \mathbb{Z} & n = 0 \\ 0 & n > 0 \end{cases}$
同调群的基本性质
1. 令 $\set{X_{\alpha}}_{\alpha \in I}$ 是 $X$ 的道路连通分支，则 $X$ 的同调群 $H_n(X) = \bigoplus_{\alpha \in I} H_n(X_\alpha)$
2. 如果 $X \neq \varnothing$ 道路连通，则 $H_0(X) = \mathbb{Z}$。进一步的，对一般的 $X$，有 $H_0(X) = \bigoplus_{\alpha \in I} \mathbb{Z}$
证明：
令 $\sigma: \Delta^n \to X$，则存在某个 $\alpha \in I$ 使得 $\sigma(\Delta^n) \subseteq X_\alpha$.

那么就有 $C_n(X) = \bigoplus_{\alpha \in I} C_n(X_\alpha)$.

更进一步，对于取边界映射有 $\partial_n(C_n(X_\alpha)) \subseteq C_{n - 1}(X_\alpha)$.

则 $\ker \partial_n = \bigoplus_{\alpha \in I} \ker (\partial_n|_{C_{n}(X_\alpha)})$，$\text{Im} \partial_{n + 1} = \bigoplus_{\alpha \in I} \text{Im} (\partial_{n + 1}|_{C_{n + 1}(X_\alpha)})$

于是 $H_n(X) = \bigoplus_{\alpha \in I} H_n(X_\alpha)$.
可以发现 $H_0(X) = C_0(X) / \text{Im} \partial_1$.

定义映射 $\varepsilon: C_0(X) \to \mathbb{Z}$，其中 $\varepsilon(\sum_i n_i \sigma_i) = \sum_i n_i$，故 $\varepsilon$ 是一个满射。

只要证明 $\ker \varepsilon = \text{Im} \partial_1$.

任取 $\sigma: \Delta^1 \to X$，有 $\varepsilon(\partial_1(\sigma)) = \varepsilon(\sigma|_{[v_1]} - \sigma|_{[v_0]}) = 1 - 1 = 0$，故 $\text{Im} \partial_1 \subset \ker \varepsilon$.

反过来，如果存在 $\varepsilon(\sum_i n_i \sigma_i) = 0$，根据 $\varepsilon$ 定义这也就意味着 $\sum_i n_0 = 0$，$\sigma_i(\Delta^0)$ 是 $X$ 中的一个点.

固定一个点 $x_0 \in X$，令 $\gamma_i: \Delta^1 \to X$（因为 $\Delta^1$ 就是一个线段，可以理解为 $\Delta^1 = I = [0, 1]$，所以 $\gamma_i$ 本质上就是一个道路），且有 $\gamma_i(0) = x_0$，$\gamma_i(1) = \sigma(\Delta^0)$ （$X$ 道路连通）。

令 $\sigma_0(\Delta^0) = x_0$，则 $\partial_1 \gamma_i = \sigma_i - \sigma_0$，进一步可以推出 $\partial_i(\sum_i n_i \gamma_i) = \sum_i n_i \sigma_i - \sum_i n_i \sigma_0 = \sum_i n_i \sigma_i - (\sum_i n_i) \sigma_0 = \sum_i n_i \sigma_i$ （$\sum_i n_i = 0$）

所以 $\sum_i n_i \sigma_i \in \text{Im} \partial_1$，故 $\ker \varepsilon \subset \text{Im} \partial_1$。

因此 $\ker \varepsilon = \text{Im} \partial_1$，进一步有 $C_0(X) / \ker \varepsilon = \mathbb{Z} = C_0(x) / \text{Im} \partial_1 = H_0(X)$.
定义：约化同调群 (Reduced Homology)

考虑链复形 $\cdots \to C_2(X) \xrightarrow{\partial_2} C_1(X) \xrightarrow{\partial_1} C_0(X) \xrightarrow{\varepsilon} \mathbb{Z} \to 0$，我们已经说明过 $\varepsilon$ 为满射。

令 $\tilde H_n$ 是这个链复形的同调，称为 $X$ 的约化同调群 (Reduced Homology)。

其中 $H_n(X) = \begin{cases} \tilde H_n(X) & n \geqslant 1 \\ \tilde H_n(X) \oplus \mathbb{Z} & n = 0 \end{cases}$
连续映射诱导同调群上的群同态

对连续映射 $f: X \to Y$，我们想要定义一个群同态 $f_{\star}: H_n(X) \to H_n(Y)$.

对于 $X$ 中的一个 $n$-单形 $\sigma: \Delta^n \to X$，定义 $f_\#(\sigma): \Delta^n \to Y$ 是 $Y$ 中的一个 $n$-单形，其中 $f_\#:= f \circ \sigma: \Delta^n \to Y$.

则我们可以线性延拓 $f_\#$ 得到 $f_\#(\sum_i n_i \sigma_i) := \sum_i n_i f_\#(\sigma_i)$.

那么我们就得到了一个同态 $f_\#: C_n(X) \to C_n(Y)$.

目前我们得到了一个自由 Abel 群上的群同态，我们接下来将说明这个群同态同时也是同调群上的：
- 引理：$f_\#$ 与取边界可交换
  
  $f_\#\partial = \partial f_\#$
  
  这就是说，对 $X$ 中的单形取边界，再映射到 $Y$，和先从 $X$ 映射到 $Y$ 再取边界，结果相同。换句话就是，取边界和映射是可交换的，如下面的交换图表：
  
  图表中的每一个正方形都是可以交换的。
  
  证明：
  
  $\begin{aligned} f_\#\partial (\sigma) &= f_\#(\sum_i (-1)^i \sigma|_{[v_0, \cdots, \hat v_i, \cdots, v_n]}) \\ &= \sum_i (-1)^i f_\#(\sigma|_{[v_0, \cdots, \hat v_i, \cdots, v_n]}) \\ &= \sum_i (-1)^i f\circ \sigma|_{[v_0, \cdots, \hat v_i, \cdots, v_n]} \\ &= \partial (f_\#(\sigma)) \end{aligned}$
应用引理，我们接下来构造 $f_\star$.

令 $\alpha \in Z_n(X) = \ker \partial_n$，则 $\partial (f_\#(\alpha)) = f_\#(\partial(\alpha)) = 0$，这说明 $f_\#(\text{cycles}) = \text{cycles}$

同时，由于 $f_\#(\partial \beta) = \partial(f_\#(\beta))$，这说明 $f_\#(\text{boundaries}) = \text{boundaries}$

因此，因为 $H_n(X) = Z_n(X) / B_n(X), H_n(Y) = Z_n(Y) / B_n(Y)$，所以 $f_\#$ 诱导了一个商群的同态 $f_\star: H_n(X) \to H_n(Y)$。

令 $\alpha \in Z_n(X)$，令 $[\alpha]$ 是 $\alpha$ 在 $H_n(X) = Z_n(X) / B_n(X)$ 中的像（商群中的等价类）

则根据之前的构造，我们可以得到 $f_\star([\alpha]) = [f_\# (\alpha)] \in H_n(Y)$（因为 $f_\# (\alpha) \in Z_n(Y)$）
- 注：链映射——代数层面上 $f_\star$ 的推广
  
  令 $C_\cdot = (\cdots \to C_{n + 1} \xrightarrow{\partial_{n + 1}} C_n \xrightarrow{\partial_{n}} C_{n - 1} \to \cdots)$，$D_\cdot = \cdots \to D_{n + 1} \xrightarrow{\partial_{n + 1}} D_n \xrightarrow{\partial_{n}} D_{n - 1} \to \cdots$ 是两个链复形。
  
  定义链映射(chain map) $f: C_\cdot \to D_\cdot$ 包含这些群同态：$f_n: C_n \to D_n$ 满足 $\partial f_n = f_{n - 1} \partial$.
  
  也就是如下的交换图表：
  
  形式上讲，链映射就是一条链到另一条链的映射，并且满足上面图表是可以交换的。
  
  链映射 $f$ 可以诱导一个群同态 $f_\star = H_n(C_\cdot) \to H_n(D_\cdot)$，$\forall n$.
总结：连续映射诱导同调群同态的性质
1. 如果 $X \xrightarrow{g} Y \xrightarrow{f} Z$，则 $(f\circ g)_\star = f_\star \circ g_{\star}$.
2. 对 $X \xrightarrow{id_X} X$，有 $(id_X)_{\star} = id_{H_n(X)}$，$\forall n$.
证明：
1. 带入定义，有 $(f \circ g)_\star = [(f \circ g)_\#(\alpha)] = [f \circ g \circ \alpha] = [f_\# g_\# (\alpha)] = f_\star g_\star ([\alpha])$.
2. $(id_X)_\star([\alpha]) = [(id_X)_\# (\alpha)] = [id_X \circ \alpha] = [\alpha]$.
- 注：拓扑空间到 Abel 群范畴的函子
  
  我们实际上构造了一个函子 $H_n$，它从拓扑空间的范畴映射到了 Abel 群的范畴：
  
  $X$ 拓扑空间 $\longmapsto$ $H_n(X)$
  
  连续映射 $f: X \to Y$ $\longmapsto$ 连续映射 $f_\star: H_n(X) \to H_n(Y)$
  
  使得 $(fg)_{\star} = f_\star g_\star$ 且 $(id_{X})_\star = id_{H_n(X)}$.
定理：同伦的映射对应相同的同调群同态

对于两个同伦映射 $f, g: X \to Y$，有 $f_\star = g_\star: H_n(X) \to H_n(Y)$。

证明：

构造 $F: X \times I \to Y$，使得 $f \underset{F}\simeq g$

此时我们想要的是高一维的 $\Delta^n \times I$ 取边界，但是 $\Delta^n \times I$ 本身不是单形，因此，我们首先想要将 $\Delta^n \times I$ 划分为数个 $(n+1)$ -单形。

我们先来看一个二维情形的例子，下图中橙色三角面与蓝色三角面将三棱柱剖分成了若干个三棱锥，即三维单形：

一般性地，令 $\Delta^n \times \set{0} = [v_0, \cdots, v_n]$，$\Delta^n \times \set{1} = [w_0, \cdots, w_n]$（图中棱柱的上下底面），使得 $v_i$ 和 $w_i$ 落在同一个投影映射 $\Delta^n \times I \to \Delta^n$ 的像中。

考虑一个 $n$-单形 $[v_0, \cdots, v_i, w_{i + 1} \cdots w_n]$，它是线性函数 $\varphi_i: \Delta^n \to I; \varphi_i(t_0, \cdots, t_n) = t_{i+1} + \cdots + t_n$，其中 $t_0, \cdots, t_n$ 是重心坐标（$\sum_{i = 0}^n t_i = 1$）的图像。

我们可以发现 $0 = \varphi_n \leqslant \varphi_{n - 1} \leqslant \varphi_{n - 2} \leqslant \cdots \leqslant \varphi_0 \leqslant \varphi_{-1} = 1$.

考虑 $\varphi_i$ 和 $\varphi_{i - 1}$ 之间的区域，这个区域就是一个 $(n+1)$-单形 $[v_0, \cdots, v_i, w_i, \cdots, w_n]$.

通过这些 $\varphi_i$，我们就把 $\Delta^n \times I$ 切分成了数个 $(n+1)$-单形 $[v_0, \cdots, v_i, w_i, \cdots, w_n]$ （其中 $0 \leqslant i \leqslant n$）的并。
- 定义：棱柱映射 (Prism Map)
  
  定义棱柱映射 (Prism Map) $P: C_n(X) \to C_{n + 1}(Y)$，$P(\sigma) := \sum_i (-1)^i F \circ (\sigma \times id_I)|_{[v_0, \cdots, v_i, w_i, \cdots, w_n]}$.
  
  其中 $\sigma: \Delta^n \to X$
  
  事实上，考察 $\Delta^n \times I \xrightarrow{\sigma\ \times id_I} X \times I \xrightarrow{F} Y$ ，也就是说某种意义上 $P$ 给出了一个 $\Delta^n(X)\to\Delta^{n+1}(X\times I)\to Y$ 的关系。
- 棱柱映射的性质
  
  $\partial P = g_\# - f_\# - P \partial$ $(\star)$
  
  下图表述了这种关系：
  
  其中 $\partial P$ 是棱柱边界，$g_\#$ 是上底面的边界，$f_\#$ 是下底面的边界，$P\partial$ 是棱柱侧面的边界。
  
  证明：
  
  $\begin{aligned}\partial P(\sigma) = &\sum_{j \leqslant i} (-1)^i (-1)^j F \circ (\sigma \times id_I)|_{[v_0, \cdots, \hat v_j \cdots, v_i, w_i, \cdots, w_n]} +\\ &\sum_{j \geqslant i} (-1)^{i} (-1)^{j + 1} F \circ (\sigma \times id_I)|_{[v_0, \cdots, v_i, w_i, \cdots, \hat w_j, \cdots, w_n]}\end{aligned}$.
  
  可以发现第一个求和中的 $i = j = k$ 项会和第二个求和中的 $i = j = k - 1$ 消掉。
  
  剩余的 $i = j$ 的项就是 $F \circ (\sigma \times id_I)|_{[\hat v_0, w_0, \cdots, w_n]} - F \circ (\sigma \times id_I)|_{[v_0, \cdots, v_n, \hat w_n]}$，其中第一项是上底面的边界，第二项是下底面的边界。
  
  由于
  
  $\begin{aligned}P \partial(\sigma) = &\sum_{i < j} (-1)^i (-1)^j F \circ (\sigma \times id_I)|_{[v_0, \cdots, \hat v_j \cdots, v_i, w_i, \cdots, w_n]} +\\&\sum_{j > i} (-1)^{i} (-1)^{j + 1} F \circ (\sigma \times id_I)|_{[v_0, \cdots, v_i, w_i, \cdots, \hat w_j, \cdots, w_n]}\end{aligned}$
  
  ，于是所有的 $i \neq j$ 的项正好就等于 $-P \partial(\sigma)$.
  
  这证明了式子 $(\star)$.
令 $\alpha \in Z_n(X)$，由 $(\star)$ 可以得到 $g_\#(\alpha) - f_\#(\alpha) = \partial P(\alpha) + P \partial(\alpha) = \partial P(\alpha)$，它是一个边界。

故 $g_\#(\alpha)$ 和 $f_\#(\alpha)$ 是同调的。

进一步的，于是有 $f_\star([\alpha]) = [f_\#(\alpha)] = [g_\#(\alpha)] = g_\star([\alpha])$.
推论：同伦等价诱导同调群同构

如果 $f: X \to Y$ 是一个同伦等价，那么 $f_\star: H_n(X) \to H_n(Y)$ 是一个同构。

也就是说，同伦等价的区间有同构的同调群。

我们将在下节课证明它。

22. 正合取边界映射

同调群

回忆：同伦等价诱导同调群同构

对于两个同伦映射 $f, g: X \to Y$，有 $f_\star = g_\star: H_n(X) \to H_n(Y)$。

推论：如果 $f: X \to Y$ 是一个同伦等价，那么 $f_\star: H_n(X) \to H_n(Y)$ 是一个同构。

证明：

令 $g:Y\to X$ 是 $f$ 的同伦逆，即 $g\circ f\simeq id_X,f\circ g \simeq id_Y$.

考虑 $f_\star\circ g_\star$，它等于 $(f\circ g)_\star=(id_Y)_\star=id_{H_n(Y)}$.

同理 $g_\star\circ f_\star=id_{H_n(x)}$. 因此 $f_\star$ 是一个同构（$f_\star$ 与 $g_\star$ 是互逆的两个同构）。
- 注：将主定理的证明推广到代数层面
  
  考虑两个链复形 $C_\cdot=(\cdots\to C_{n+1}\xrightarrow{\partial} C_n\xrightarrow{\partial}C_{n-1}\to\cdots)$
  
  与 $D_\cdot=(\cdots\to D_{n+1}\xrightarrow{\partial} D_n\xrightarrow{\partial} D_{n-1}\to\cdots)$
  
  考虑两个链映射 $f_\#$ 与 $g_\# :C_\cdot\to D_\cdot$（$\partial f_\#=f_\#\partial,\partial g_\#=g_\# \partial$）.
  
  假设 $\exists$ 群同态 $P:C_n\to D_{n+1},\forall n$，使得 $\partial P+P\partial=g_\#-f_\#$，则 $f_\star=g_\star (H_n(C_\cdot)\to H_n(D_\cdot)),\forall n$.
  
  我们将这个映射 $P$ 称为 $f_\#$ 到 $g_\#$ 的链同伦 (Chain Homotopy)。
  
  这就是下图：
- 注：结论对约化同调群也成立
  
  回忆：对 $f:X\to Y$，我们有 $f_\star:\tilde H_n(X)\to\tilde H_{n}(Y)$.
  
  上面的结论对约化同调群诱导出的 $f_\star$ 也成立。
  
  成立的原因：我们有如下图链映射：
  
  可以验证出它是交换的，因此上面的结论确实成立。
  
  因此若 $f,g:X\to Y$ 是同伦的，则 $f_\star=g_\star:\tilde H_n(X)\to\tilde H_n(y)$.

同调代数 (Homological Algebra)

正合 (Exact)

考虑一个 Abel 群群同态的序列 $A_\cdot=(\cdots\to A_{n+1}\xrightarrow{f_{n+1}} A_n\xrightarrow{f_n}A_{n-1}\to\cdots)$

我们称这个序列在 $A_n$ 处是正合 (Exact) 的，若 $\ker f_n=\text{Im} f_{n+1}$.

我们称序列整体是正合的，若它对每一个 $A_n$ 都是正合的。
一些正合列的例子

$0\to A\xrightarrow{f} B$ 在 $A$ 处正合 $\Leftrightarrow$ $f$ 是一个单射。

$A\xrightarrow{f}B\to 0$ 在 $B$ 处正合 $\Leftrightarrow$ $f$ 是一个满射。

$0\to A\xrightarrow{f}B\to0$ 正合 $\Leftrightarrow$ $f$ 是一个同构。

$0\to A\xrightarrow{f}B\xrightarrow{g}C\to 0$ 正合 $\Leftrightarrow$ $f$ 是单射，$g$ 是满射，$\ker g=\text{Im} f$.

我们称最后一种情况为短正合列 (Short Exact Sequence).

在这种情况下，$A\cong \ker g, C\cong B/f(A)$.

考虑 $A_\cdot,B_\cdot,C_\cdot$ 是三个链复形，考虑序列 $0\to A_\cdot\xrightarrow{f_\cdot}B_\cdot\xrightarrow{g_\cdot} C_\cdot\to 0$

其中 $f_\cdot,g_\cdot$ 是链映射，即 $f_\cdot=(f_n)_{n\in\mathbb{Z}},g_\cdot=(g_n)_{n\in \mathbb{Z}}$

$0$ 代表 $0$ 复形，即 $\cdots \to 0\to 0\to 0\to \cdots$

$f_n:A_n\to B_n,g_n:B_n\to C_n, f_n\partial = \partial f_{n+1}, g_n\partial = \partial g_{n+1}$.

我们将刚才的序列称作是链复形的短正合列，若 $\forall n\in \mathbb{Z}$，有 $0\to A_n\xrightarrow{f_n} B_n\xrightarrow{g_n} C_n\to 0$ 都是短正合列。

因为 $f_\cdot,g_\cdot$ 是链映射，因此它们诱导了同调群的群同态 $f_\star:H_n(A_\cdot)\to H_n(B_\cdot)$ 以及 $g_\star:H_n(B_\cdot)\to H_n(C_\cdot)$.

问：将取 $\star$ 操作作用在短正合列之后，所得到的还是短正合列吗？即 $0\to H_n(A_\cdot)\xrightarrow{f_\star} H_n(B_\cdot)\xrightarrow{g_\star}H_n(C_\cdot)\to 0$ 是正合列吗？

答案是否定的。

我们还需要进行如下的关键构造：定义边界映射 (Boundary Map)，请注意不要与之前的定义混淆 $\bar\partial:H_n(C_\cdot)\to H_{n-1}(A_\cdot)$，这也就形如：

任取圈(取边界为 $0$) $c\in C_n$，由于 $g_n$ 是一个满射，于是 $\exists b\in B_n$ 使得 $g_n(b)=c$.

由于 $g_{n-1}\partial(b)=\partial g_n(b)=\partial(c)=0$，因此 $\partial(b)\in\ker b_{n-1}=\text{Im}(f_{n-1})$，这就是说 $\exists a\in A_{n-1}$，使得 $f_{n-1}(a)=\partial(b)$.

$f_{n-2}(\partial(a))=\partial f_{n-1}(a)=\partial(\partial(b))=0$，由于 $f_{n-2}$ 是一个单射，因此 $\partial(a)=0$，也就是说 $a$ 是一个圈。

因此我们可以定义取边界映射：$\bar\partial:H_n(C_\cdot)\to H_{n-1}(A_\cdot)$ 为 $\bar\partial([c])=[a]$.
另一个取边界映射（请注意区分 $\partial$ 记号）

$\bar\partial :H_n(C_\cdot)\to H_{n-1}(A_\cdot)$ 中 $\bar\partial([c])=[a]$ 是良定义的群同态。

证明：
1. 由于 $f_{n-1}$ 是单射，因此 $a$ 是被 $\partial (b)$ 唯一确定的；
2. 考虑 $b\in B_n$ 使得 $g_n(b)=c$. 如果我们选择另一个 $b'\in B_n$ 使得 $g_n(b')=c$.
从而 $b'-b\in \ker g_n$，根据正合性，$\ker g_n=\text{Im} f_n$，也就是说 $\exists a'\in A_n$ 使得 $b'-b=f_n(a')$.

因此 $f_{n-1}(a+\partial a')=f_{n-1}(a)+f_{n-1}(\partial a')=\partial b+\partial f_n(a')=\partial b'$.

因此如果我们把 $b$ 换成 $b'$，我们就将 $a$ 换成了 $a+\partial a'$，但是 $[a]=[a+\partial a']$.
1. 考虑 $c+\partial c'$，其中 $c'\in C_{n+1}$.（$[c]=[c+\partial c']$）
由于 $g_{n+1}$ 是满射，$\exists b'\in B_{n+1}$ 使得 $g_{n+1}(b')=c'$.

$c+\partial c'=c+\partial(g_{n+1}(b'))=c+g_{n}\partial b'=g_n(b+\partial b')$.

然而 $f_{n-1}(a)=\partial b=\partial(b+\partial b')$，于是 $f_{n-1}(a)$ 没有变化，于是 $a$ 也没有变化（单射）。

根据 (1) (2) (3)，我们能知道 $\bar\partial$ 确实是良定义的。
- 注：
  
  这里课上板书中 $\bar\partial$ 与 $\partial$ 都写作 '$\partial$'，笔者在记录时为了区分加了一个 $\text{bar}$. 我不敢保证每个地方都做好了这个区分，因此阅读笔记时敬请甄别。
  
  实际上，$\bar\partial$ 也是某种意义上的取边界映射。
下面我们验证它是一个群同态。

令 $\bar\partial [c_1]=[a_1],\bar\partial [c_2]=[a_2]$，有 $g_n(b_1)=c_1,g_n(b_2)=c_2$，$f_{n-1}(a_1)=\partial b_1,f_{n-1}(a_2)=\partial b_2$.

于是 $g_n(b_1+b_2)=c_1+c_2$，$f_{n-1}(a_1+a_2)=\partial b_1+\partial b_2=\partial(b_1+b_2)$.

于是 $\bar\partial ([c_1]+[c_2])=([a_1]+[a_2])=\bar\partial [c_1]+\bar\partial [c_2]$.
同调群的长正合列 (Long Exact Sequence of Homology)

在我们定义好 $\bar\partial$ 后，我们得到了一个序列：$\cdots \to H_n(C_\cdot)\xrightarrow{\bar\partial} H_{n-1}(A_\cdot)\xrightarrow{f_\star} H_{n-1}(B_\cdot)\xrightarrow{g_\star}\cdots$，这个序列是一个正合序列。

将其称为同调群的长正合列 (Long Exact Sequence of Homology)。

证明：
1. 我们说明 $f_\star$ 与 $g_\star$ 有 $\text{Im} f_\star=\ker g_\star$
$g_\cdot\circ f_\cdot=0$，因此 $(g_\cdot\circ f_\cdot)_\star=(g_\star\circ f_\star)=0$.

这告诉我们 $\text{Im} f_\star\subset \ker g_\star$.

取 $[b]\in \ker g_\star$，$b\in B_n$，$\partial b=0$，则 $g_n(b)=\partial c'$ 对于某个 $c'\in C_{n+1}$.

又由 $g_{n+1}$ 是满射，$c'=g_{n+1}(b')$，对于某个 $b'\in B_{n+1}$.

因此 $g_n(b-\partial b')=g_n(b)-g_n(\partial b')=g_n(b)-\partial g_{n+1}(b')=\partial c'-\partial c'=0$.

这告诉我们 $\exists a\in A_n$，使得 $b-\partial b'= f_n(a)$. (正合性)

$f_{n-1}(\partial a)=\partial f_n(a)=\partial (b-\partial b')=\partial b=0$.

由于 $f_{n-1}$ 是一个单射，因此 $\partial a=0,a$ 是一个圈。

因此 $f_\star [a]=[b-\partial b']=[b]$，因此 $[b]\in \text{Im} f_\star$，$\ker g_\star\subset \text{Im} f_\star$.

因此 $\ker g_\star=\text{Im} f_\star$。
1. 我们说明 $\text{Im} g_\star=\ker\bar\partial$.
根据定义，$\bar\partial [c]=[a]$ 有 $f_{n-1}(a)=\partial b$，$g_n(b)=c$.

如果 $[c]=g_\star[b]=[g_n(b)]$ 对于某个 $b$，我们选取代表元使得 $g_n(b)=c$，因此 $f_{n-1}(a)=\partial b=0$，因此 $a=0$.

因此 $\bar\partial g_\star=0$，这就是说 $\text{Im} g_\star\subseteq \ker\bar\partial$.

反过来，如果我们令 $\bar\partial [c]=0=[a]$，则 $a$ 是一个边界元，也就是说 $a=\partial a'$ 对某个 $a'\in A_n$.

因此 $\partial (b-f_n(a'))=\partial b-f_{n-1}(\partial a')=\partial b-f_{n-1}(a)=0$.

因此 $b-f_n(a')$ 确实是一个圈，我们将 $g_n$ 作用在圈上就有 $g_n(b)-g_n\circ f_n(a')=g_n(b)=c$.

这就是说 $g_\star([b-f_n(a')])=[c]$，因此 $\ker\bar\partial\subset \text{Im} g_\star$.

因此 $\ker\bar\partial =\text{Im} g_\star$.
1. 我们说明 $\text{Im}\bar\partial=\ker f_\star$.
若 $[c]=H_n(C_\cdot)$，则 $f_\star\bar\partial [c]=f_\star [a]=[f_{n-1}(a)]=[\partial b]=0$. 因此 $\text{Im} \bar\partial \subset\ker f_\star$.

反过来，令 $f_\star[a]=0$，其中 $a\in A_{n-1},\partial a=0$.

这告诉我们 $f_{n-1}(a)=\partial b$，对于某一个 $b\in B_n$，因此 $\partial g_n(b)=g_{n-1}(\partial b)=g_{n-1}\circ f_{n-1}(a)=0$. (正合性)

这就是说 $g_n(b)$ 是一个圈，因此 $\bar\partial [g_n(b)]=[a]\in \text{Im}\bar\partial$，因此 $\ker f_\star\subset \text{Im}\bar\partial$.

因此 $\text{Im}\bar\partial =\ker f_\star$.
下节课

我们将考虑 Commutative Diagram.

23. 相对同调群

同调群的自然性定理

回忆

$0 \to A_\cdot \xrightarrow{f_\cdot}B_\cdot \xrightarrow{g_\cdot} C_\cdot \to 0$ 正合列可以导出

$\cdots \to H_{n+1}(C_\cdot) \xrightarrow{\bar\partial} H_n(A_\cdot) \xrightarrow{f_\star} H_n(B_\cdot) \xrightarrow{g_\star} H_n(C_\cdot) \xrightarrow{\bar\partial} H_{n-1}(A_\cdot) \to \cdots$
两个链映射的交换性

考虑下面链映射的交换图表：

图表中的正方形是交换的。

我们将来在拓扑中想要考察导出的两个长正合列之间的关系。

在代数上讲，这就是说这是两行短正合列，我们接下来要考察两个长正合列：

我们想要知道，这个长正合列图表是交换的吗？
自然性定理 (Normality Theorem)

上面的长正合列图表确实是交换的。

证明：

两个红色的交换性是比较简单的：

由于 $\beta_\cdot\circ f_\cdot=f'_\cdot\circ \alpha_\cdot$，因此 $\beta_{\star\cdot}\circ f_{\star\cdot}= f'_{\star\cdot}\circ \alpha_{\star\cdot}$.

第二个红色类似。

对于绿色正方形，令 $c \in C_n$ 是一个圈，则 $\bar \partial([c]) = [a]$，其中 $a \in A_{n - 1}$，满足 $f_{n-1}(a) = \partial b$，$c = g_n(b)$

那么就有 $\gamma_n(c) = \gamma_n \circ g_n(b) = g_n' \beta_n(b)$

而对于 $f_{n-1}$，我们可以得到 $f'_{n-1} \circ \alpha_{n-1}(a) = \beta_{n-1} f_{n-1} (a) = \bar \beta_{n-1} \bar\partial b = \partial \beta_n(b)$

由 $\bar \partial$ 的定义，$\bar \partial [\gamma_n(c)] = [\alpha_{n-1}(a)]$，左边等于 $\bar\partial \gamma_\star[c]$，右边等于 $\alpha_\star(a)$，因此我们就得到了 $\bar\partial \gamma_\star[c] = \alpha_\star \bar\partial[c]$

相对同调群 (Relative Homology)

相对同调群 (Relative Homology)

“相对性”：大空间 $X$ “相对于” 子空间 $A$ 的同调群。

令 $X$ 是一个拓扑空间，$A \subset X$。

令商群 $C_n(X, A) := C_n(X) / C_n(A)$，考虑取边界映射 $\partial: C_n(X) \to C_{n-1}(X)$。如果将取边界映射限制在子群 $C_n(A)$ 中，显然有 $\partial(C_n(A)) \subset C_{n-1}(A)$。

这就自然诱导出了一个商群的取边界映射 $\partial: C_n(X, A) \to C_{n-1}(X, A)$，这是两个商群之间的同态。

由于在链复形 $C_\cdot(X) = \set{C_n(X)}_n$ 中有 $\partial^2 = 0$，那么在 $C_\cdot(X, A) = \set{C_n(X, A)}_n$ 中自然也有 $\partial^2 = 0$。

因此 $C_\cdot(X, A)$ 确实是一个链复形。

$H_n(C_\cdot(X, A))$ 被叫做相对同调群 (Relative Homology)，记为 $H_n(X, A)$。
- 相对圈、相对边界与平凡元
  - 相对圈 (relative cycle)：$\alpha \in C_n(X)$ 使得 $\partial \alpha \in C_{n-1}(A)$，相当于取边界落到了商复形的 0 中。
  - 相对边界 (relative boundary)：$alpha = \partial \beta + \gamma$，其中 $\beta \in C_{n+1}(X)$，$\gamma \in C_n(A)$
  - 一个相对圈 $\alpha$ 在 $H_n(X, A)$ 中是 trivial 的当且仅当 $\alpha$ 是一个相对边界.
相对同调群的正合列

我们可以定义短正合列 $0 \to C_\cdot (A) \xrightarrow{i_\cdot} C_\cdot (X) \xrightarrow{j_\cdot} C_\cdot(X, A) \to 0$，其中 $i_\cdot$ 是嵌入映射，$j_\cdot$ 是商映射。

我们也可以从这个短正合列导出长正合列：

$\cdots \to H_{n}(A) \xrightarrow{i_\star} H_n(X) \xrightarrow{j_\star} H_n(X, A) \xrightarrow{\partial} H_{n-1} (A) \to \cdots$

在末尾是 $\cdots \to H_0(A) \to H_0(X) \to H_0(X, A) \to 0$

如果对于 $H_n(X, A) = 0, \forall n$，（回忆 $0 \to A \xrightarrow{f} B \to 0$ 正合，那么 $f$ 是单射、满射，即 $f$ 是同构）

那么 $i_\star: H_n(A) \to H_n(X)$ 是一个同构 $\forall n$.
- 注：约化版本的正合列
  
  对于 $(X, A)$ 其中 $A \neq \varnothing$。
  
  考虑短正合列 $0 \to \tilde C_\cdot (A) \xrightarrow{i_\cdot} \tilde C_\cdot (X) \xrightarrow{j_\cdot} C_\cdot (X, A) \to 0$
  
  可以发现：
  
  因此，我们就得到了一个约化版本的长正合列：
  
  $\cdots \to \tilde H_n(A) \xrightarrow{i_\star} \tilde H_n(X) \xrightarrow{j_\star} H_n(X, A) \xrightarrow{\partial} \cdots \to \tilde H_0(A) \to \tilde H_0(X) \to H_0(X, A) \to 0$
  
  这个约化版本的正合列和之前的长正合列只有 $\tilde H_0(A)$ 和 $\tilde H_0(X)$ 不同。
例：单点子群的相对同调群列

$H_n(\text{point}) = \begin{cases} \mathbb{Z} & n = 0 \\ 0 & n > 0 \end{cases}$，则 $\tilde H_n(\text{point}) = 0, \forall n$

取 $A = \set{x_0} \subseteq X$，考虑对 $(X, x_0)$ 其中 $x_0 \in X$。

由上面的长正合列，因为中间夹的 $\tilde H_n(x_0) = 0, \forall n > 0$，我们就可以得到 $H_n(X, x_0) \cong \tilde H_n(X)$。
连续映射诱导相对同调群中群同态

令 $f: (X, A) \to (Y, B)$，这个记号意味着 $A \subset X, B \subset Y, f(A) \subset B$

$f$ 诱导出 $f_\#: C_n(X) \to C_n(Y)$，那么就有 $f_\# (C_n(A)) \subseteq C_n(B)$。

所以它诱导了一个商映射 $f_\#: C_n(X, A) \to C_n(Y, B)$。

我们就得到了 $f_\star: H_n(X, A) \to H_n(Y, B)$。
同伦的映射诱导相同的相对同调群同态

令 $f, g : (X, A) \to (Y, B)$，如果存在 $F: X \times I \to Y$ 是一个同伦，使得 $f \underset{F}\simeq g$ 且 $F|_{X \times \set{t}} (A) \subseteq B, \forall t \in I$。

那么就有 $f_\star = g_\star: H_n(X, A) \to H_n(Y, B)$。

证明：

考虑棱柱映射 $P: C_n(X) \to C_{n+1}(Y)$，那么棱柱映射也就将 $C_n(A)$ 映射到 $C_{n+1}(B)$ 中。

这就诱导了一个棱柱映射 $P: C_n(X, A) \to C_{n+1}(Y, B)$。

由于 $P\partial + \partial P = g_\# - f_\#$ 在 $C_n(X)$ 上成立，取商群后同样成立。

因此 $P$ 确实是商群上的一个链同伦。

所以我们就得到了 $f_\star = g_\star: H_n(X, A) \to H_n(Y, B)$。

对连续映射 $f: (X, A) \to (Y, B)$，对于它诱导的 $f_\#$，我们可以得到如下交换图表：

根据上面的自然性定理，对诱导出的 $f_\star$ 就可以得到下面这个交换图表：
推广的长正合列 (Generalization of Long Exact Sequence)

令 $B \subset A \subset X$，有短正合列 $0 \to C_n(A, B) \to C_n(X, B) \to C_n(X, A) \to 0$

其中 $C_n(A, B) = C_n(A) / C_n(B)$，$C_n(X, B) = C_n(X) / C_n(B)$，$C_n(X, A) = C_n(X) / C_n(A)$。

看上去就跟将公共的分母 $C_n(B)$ 约掉了。

那么我们就得到了链复形的短正合列 $0 \to C_\cdot (A, B) \to C_\cdot (X, B) \to C_\cdot (X, A) \to 0$。

同样也得到了链复形的长正合列 $\cdots \to H_n(A, B) \to H_n(X, B) \to H_n(X, A) \to H_{n-1}(A, B) \to \cdots$。
链复形的同伦等价 (Homotopy Equivalences)

令 $f_\cdot: C_\cdot \to D_\cdot$ 是一个链映射，如果存在一个反向的链映射 $g_\cdot: D_\cdot \to C_\cdot$，使得 $f \circ g \simeq id_{D_\cdot}$ 且 $g \circ f \simeq id_{C_\cdot}$。

则 $f_\cdot$ 被称为链复形之间的同伦等价 (Homotopy Equivalences between Chain Complexes)。

此时 $C_\cdot, D_\cdot$ 称为同伦等价的两个复形。

它诱导出的同调群之间的同态 $f_\star: H_n(C_\cdot) \xrightarrow{\cong} H_n(D_\cdot)$ 就是一个同构。
切除定理 (Excision Theorem)

令 $Z \subset A \subset X$ 满足 $\bar{Z} \subset \mathring{A}$（$Z$ 的闭包在 $A$ 的内部）。

考虑嵌入映射 $(X - Z, A - Z) \hookrightarrow (X, A)$，那么这个嵌入映射诱导了相对同调群之间的同构 $H_n(X - Z, A - Z) \xrightarrow{\cong} H_n(X, A), \forall n$。

这是在说，在 $X$ 和 $A$ 中同时切除了一个子空间 $Z$，切前切后的同调群是同构的。

等价形式：

令 $A, B \subset X$ 满足 $A$ 和 $B$ 的内部能够覆盖 $X$。

考虑嵌入映射 $(B, A \cap B) \hookrightarrow (X, A)$，那么这个嵌入映射就诱导了一个群同构 $H_n(B, A \cap B) \xrightarrow{\cong} H_n(X, A), \forall n$。

（考虑令 $Z = A \setminus (A \cap B)$，两个说法等价）

证明：

考虑集族 $\beta = \set{U_j}_{j \in J}$ 是一族 $X$ 中的子空间，满足他们的内部构成了 $X$ 的开覆盖。

令 $C_n^\beta (X) \subset C_n(X)$，包含了链 $\sum_i n_i \sigma_i$ 使得对于每个 $\sigma_i$ 都满足 $\text{Im} \sigma_i$ 包含在某个 $U_j \in \beta$ 中。

令 $\partial: C_n(X) \to C_{n-1}(X)$ 是取边界映射。

那么就有 $\partial (C_n^\beta(X)) \subset C_{n-1}^\beta(X)$。

因此 $(C_\cdot^\beta(X), \partial)$ 是一个链复形。

将这个链复形的同调群 $H_n(C_\cdot^\beta(X))$ 记做 $H_n^\beta(X)$。
- 引理
  
  令 $i: C^\beta(X) \hookrightarrow C_\cdot (X)$ 是一个嵌入映射。
  
  如果存在一个链同伦 $\rho: C_\cdot(X) \to C^\beta(X)$ 满足 $\rho \circ i = id_{C^\beta(X)}$ 且存在另一个链同伦 $D: C_n(X) \to C_{n+1}(X)$ 满足 $\partial D + D \partial = id_{C_\cdot(X)} - i \circ \rho$。
  
  那么 $i, \rho$ 是互逆的同伦等价，且 $i_\star: H_n^\beta(X) \xrightarrow{\cong} H_n(X)$。进一步地，$i, \rho, D$ 都将 $U_j$ 的链映射到 $U_j$ 的链 $\forall U_j \in \beta$。

24. 切除定理及其应用

切除定理

回忆：切除定理

令 $Z\subset A\subset X$，$\bar Z\subset \mathring A$，则 $H_n(X-Z,A-Z)\cong H_n(X,A)$；等价地，若 $A,B\subset X$ 满足 $X=\mathring A\cup \mathring B$，则 $H_n(B,A\cap B)\cong H_n(X,A)$.
- 引理
  
  $i:C^\beta(X)\hookrightarrow C_\cdot(X)$ 嵌入映射，若 $\exists$ 链映射 $\rho:C_\cdot(X)\to C^\beta(X)$，使得 $\rho\circ i=id_{C^\beta(X)}$ 并 $\exists$ 链同伦 $D:C_n(X)\to C_{n+1}(X)$ 使得 $\partial D+D\partial = id_{C_\cdot (X)}-i\circ \rho$.
  
  更进一步地，$i,\rho,D$ 都将 $U_j$ 中的链映射到 $U_j$ 中的链。
  
  推荐文献：Hatcher Prop. 2.21，我们只解释引理的直观含义。
  
  直观含义：我们用到了一个叫做“重心重分 (Barycentric Subdivision)”的思想：
  
  本来 $\Delta$ 的像不落在某个 $U_j$ 中，如果我们如图不断切割 $\Delta$，引理证明了，我们进行有限次重心重分之后，小单形的像一定分别落在某些 $U_j$ 中，$\rho$ 的构造就是小单形的和。
切除定理的证明

证明：

我们来证明第二个等价叙述。

令 $\beta=\set{A,B}$，则 $A,B$ 的内部确实覆盖了 $X$，满足引理条件。

由上面的引理，$\exists \rho:C_\cdot(X)\to C^\beta(X)$，$D:C_n(X)\to C_{n+1}(X)$，使得 $\partial D+D\partial =id_{C_\cdot(X)}-i\circ \rho$，$\rho\circ i=id_{C_\cdot^\beta(X)}$.

由于 $\rho,D,i$ 都把 $A,B$ 中的链映射到 $A,B$，我们考虑嵌入映射 $C_n^\beta(X)/C_n(A)\hookrightarrow C_n(X)/C_n(A)$，这个嵌入是一个链间的同伦等价。

因此 $H_n(C^\beta(X)/C_\cdot(A))\cong H_n(X,A)$.

考虑映射 $C_n(B)/C_n(A\cap B)\hookrightarrow C_n^\beta(X)/C_n(A)$ 嵌入，这在链复形层面已经是一个同构了。这是因为两边的群都是自由 Abel 群，且它们的基都是 $n$-单形，且基中 $n$-单形落在 $B$ 中并不落在 $A$ 中（这就是说，两边拥有相同的基）。

因此 $H_n(B,A\cap B)\cong H_n(C^\beta(X)/C_\cdot(A))$.

同构具有传递性，因此 $H_n(B,A\cap B)\cong H_n(X,A)$.
定义：好对 (Good Pair)

令 $A\neq\varnothing$，并且 $A$ 是一个闭集。设 $\exists$ 开集 $U$ 使得 $A\subset U\subset X$，且有 $A$ 是 $U$ 的形变收缩。那么称 $(X,A)$ 是一个好对 (Good Pair)。太对了。
定理：相对同调群的几何解释

令 $(X,A)$ 是一个好对，考虑粘合映射 $q:(X,A)\to (X/A,A/A)$（这意味着将子空间 $A$ 粘合为一个点），则这个粘合映射诱导了一个同构 $q_\star:H_n(X,A)\to H_n(X/A,A/A)\cong \tilde H_n(X/A),\forall n$.

证明：

考虑 $A\subset U\subset X$，其中 $U$ 是开的且可以形变收缩到 $A$ 中。

我们有嵌入映射 $i_1:(X,A)\hookrightarrow (X,U), i_2:(X-A,U-A)\hookrightarrow(X,U)$.

这诱导了粘合空间的嵌入映射 $\bar i_1:(X/A,A/A)\hookrightarrow (X/A,U/A)$，$\bar i_2:(X/A-A/A,U/A-A/A)\hookrightarrow(X/A,U/A).$

因此有交换图表：

空间 $(X,U,A)$ 的长正合列为 $\cdots\to H_n(U,A)\to H_n(X,A)\xrightarrow{i_{1\star}} H_n(X,U)\to H_{n-1}(U,A)\to\cdots$

由于 $U$ 可以形变收缩到 $A$，因此对正合列 $H_{n+1}(U,A)\to H_n(A)\xrightarrow{\cong}H_n(U)\to H_n(U,A)$，中间的映射根据形变收缩因此是同构，因此左右两个元素都是 $0$，也就是说 $H_n(U,A)=0=H_{n-1}(U,A)$. 因此 $i_{1\star}$ 是一个同构。

类似地，我们也可以知道 $\bar i_{1\star}$ 是一个同构。

由切除定理，我们发现 $i_{2\star}$ 与 $\bar i_{2\star}$ 也是同构；

由于 $q'':X-A\to X/A-A/A$ 以及 $q'':U-A\to U/A-A/A$ 实际上都是同胚（根据定义，左边和右边剪掉的都恰好是 $A$），因此 $q''_\star$ 还是一个同构 $H_n(X-A,U-A)\to H_n(X/A-A/A,U/A-A/A)$.

于是 $q_\star=\bar i_{1\star}^{-1}\circ \bar i_{2\star} \circ q''_\star\circ i_{2\star}^{-1}\circ i_{1\star}$ 是同构，因此 $H_n(X/A,A/A)\cong H_n(X,A)$.
- 注：
  如果 $(X,A)$ 是好对，那么 $\exists$ 长正合列 $\cdots\to \tilde H_n(A)\xrightarrow{i} \tilde H_n(X)\xrightarrow{j_\star} \tilde H_n(X/A)(H_n(X,A))\xrightarrow{\partial} \tilde H_{n-1}(A)\to\cdots$，这也就是说本来长正合列的相对同调群可以被约化同调群替代。
定理的应用：同调群的计算（举例）
- Wedge Sum 空间的同调群
  
  给出一族拓扑空间 $X_\alpha$，其中 $\alpha\in I$. 我们取 $x_\alpha\in X_\alpha$ 使得 $(X_\alpha,\set{x_\alpha})$ 是一个好对， $\forall \alpha$.
  
  考虑嵌入映射 $i_\alpha:X_\alpha\hookrightarrow \bigvee_{\alpha\in I} X_\alpha$，这诱导了同构 $\displaystyle{\bigoplus_{\alpha\in I} i_{\alpha\star}:\bigoplus_{\alpha\in I}\tilde H_n(X_\alpha)\to \tilde H_n(\bigvee_{\alpha\in I} X_\alpha)}$.
  
  证明：
  
  考虑空间 $X=\bigsqcup_{\alpha\in I}X_\alpha$，$A=\bigsqcup_{\alpha\in I}\set{x_\alpha}$，考虑 $X/A$，根据定义，它就是 $\bigvee_{\alpha\in I} X_\alpha$.
  
  因此有
  
  $\bigoplus_{\alpha\in I}\tilde H_n(X_\alpha)\cong \bigoplus_{\alpha\in I} H_n(X_\alpha,\set{x_\alpha})\cong H_n(\bigsqcup_{\alpha\in I} X_\alpha,\bigsqcup_{\alpha\in I}\set{x_\alpha})$
  
  $=H_n(X,A)\cong \tilde H(X/A)=\tilde H_n(\bigvee_{\alpha\in I}X_\alpha)$.
- 推论：$n$ 维球面的同调群
  
  $H_i(S^n)=\begin{cases}\mathbb{Z}&i=0,n\\0&i\neq 0,n\end{cases}$
  
  证明：
  
  设 $D^n$ 是一个 $n$ 维实心球，令 $(X,A)=(D^n,\partial D^n=S^{n-1})$，于是 $X/A=S^n$.
  
  我们就有长正合列 $\cdots\to \tilde H_i(S^{n-1})\to \tilde H_i(D^n)\to\tilde H_i(S^n)\xrightarrow{\partial} \tilde H_{i-1}(S^{n-1})\to\cdots$
  
  因为 $H_i(D^n)=0$（$D^n$ 是可缩空间），于是 $\partial:\tilde H_i(S^n)\to\tilde H_{i-1}(S^{n-1})$ 是一个同构。
  
  根据归纳，若 $i\neq 0$，则 $\tilde H_i(S^n)\cong \tilde H_{i-n}(S^0)=\begin{cases}\mathbb{Z}&i=n\\0&i\neq n\end{cases}$
  
  此外，当 $i=0$，$H_0(S^n)=\mathbb{Z}$，从而得出结论。
- 推论：任意维数的 Brouwer 不动点定理
  
  沿用之前的证明方法，假设 $f(x)\neq x,\forall x\in D^n$，则可以构造出 $g:D^n\to S^{n-1}$，使得 $g|_{S^{n-1}}=id_{S^{n-1}}$. （射线法）
  
  考虑复合映射 $S^{n-1}\hookrightarrow D^n\xrightarrow{g} S^{n-1}$，因此 $g_\star\circ i_\star =id_{H_{n-1}(S^{n-1})}$，其中 $i$ 是嵌入映射。
  
  然而 $H_{n-1}(S^{n-1})\cong \mathbb{Z}, H_{n-1}(D^n)=0 (n\geq 2)$，这导出了矛盾。
- 推论：同胚的开集维数相同
  
  考虑 $\varnothing\neq U\subset \mathbb{R}^m$ 开集，$\varnothing\neq V\subset \mathbb{R}^n$ 开集，若 $U$ 与 $V$ 是同胚的，则 $m=n$.
  
  证明：
  
  任取 $x\in U$，由切除定理有 $H_k(U,U-\set{x})\cong H_k(\mathbb{R}^m,\mathbb{R}^m-\set{x})$.
  
  考虑长正合列 $\cdots\to \tilde H_k(\mathbb{R}^m-\set{x})\to \tilde H_k(\mathbb{R}^m)\to H_k(\mathbb{R}^m,\mathbb{R}^m-\set{x})\to \tilde H_{k-1}(\mathbb{R}^m-\set{x})\to\cdots$
  
  由于 $\tilde H^k(\mathbb{R}^m)=0$（可缩），有 $H_k(\mathbb{R}^m,\mathbb{R}^m-\set{x})\cong \tilde H_{k-1}(\mathbb{R}^m-\set{x})$，且 $\mathbb{R}^m-\set{X}\simeq S^{n-1}$
  
  从而 $H_k(\mathbb{R}^m,\mathbb{R}^m-\set{x})\cong \tilde H_{k-1}(S^{n-1})=\begin{cases}\mathbb{Z}&k=m\\0&k\neq m\end{cases}$
  
  假设 $\exists$ 同胚 $h:U\to V$，一定有 $H_k(U,U-\set{x})\cong H_k(V,V-\set{h(x)})=H_k(\mathbb{R}^n,\mathbb{R}^n-\set{h(x)})$.
  
  比较上下两个结构，我们有 $H_k(\mathbb{R}^m,\mathbb{R}^m-\set{x})=H_k(\mathbb{R}^n,\mathbb{R}^n-\set{h(x)})$.
  
  因此 $m=n$.
- 注：局部同调群 (Local Homology)
  
  $\forall x\in X$，我们将 $H_n(X,X-\set{x})$ 称为局部同调群 (Local Homology)，如果 $\set{x}$ 在空间中是个闭集，由切除定理有 $\forall$ 邻域 $x\in U$，有 $H_n(X,X-\set{x})=H_n(U,U-\set{x})$.
- 例：球与球面的相对同调群的生成元
  
  $H_n(D^n,\partial D^n)=\tilde H_n(S^n)=\mathbb{Z}$，我们希望具体描述这个群的生成元。
  
  我们将 $D^n$ 与 $\partial D^n$ 看成 $n$ 维单形 $\Delta^n$ 与它的边界 $\partial \Delta^n$.
  
  考虑奇异单形 $i_n:\Delta^n\to \Delta^n$ 是恒等映射，则 $\partial i_n$ 是 $\Delta^n$ 边界里面的链，因此 $i_n$ 在商复形 $C_n(\Delta^n)/C_n(\partial \Delta^n)$ 中看是一个圈。
  
  结论：$[i_n]$ 就是我们要取的 $H_n(D^n,\partial D^n)$ 的生成元。
  
  证明：
  
  归纳法。当 $n=0$ 的时候是显然的；
  
  令 $\Lambda\subset \Delta^n$ 是一个 $\Delta^n$ 除了其中一个 $n-1$ 维面以外的其他面并起来：
  
  考虑 $(\Delta^n,\partial \Delta^n,\Lambda)$，可以得到一个长正合列：
  
  $\cdots\to H_n(\partial\Delta^n,\Lambda)\to H_n(\Delta^n,\partial \Delta^n)\xrightarrow{\partial}H_{n-1}(\partial \Delta^n,\Lambda)\to H_{n-1}(\Delta^n,\Lambda)\to\cdots$
  
  因为 $\Delta^n$ 可以形变收缩到 $\Lambda$，因此 $H_n(\Delta^n,\Lambda)=0$.
  
  于是 $\partial$ 给出了 $H_n(\Delta^n,\Lambda)\cong H_{n-1}(\partial \Delta^n,\partial \Delta^n)$
  
  考虑嵌入映射 $(\Delta^{n-1},\partial \Delta^{n-1})\xrightarrow{\varphi}(\partial \Delta^n,\Lambda)$，它给出的同构是
  
  $\tilde H_{n-1}(\Delta_{n-1}/\partial\Delta^{n-1})=H_{n-1}(\Delta^n,\partial \Delta^{n-1})\xrightarrow{\cong}H_{n-1}(\partial\Delta^n,\Lambda)= \tilde H_{n-1}(\partial \Delta^n/\Lambda)$
  
  $\varphi$ 实际上给出的是一个 $S^{n-1}\to S^{n-1}$ 的映射；
  
  于是 $\varphi_\star^{-1}\partial [i_n]=[i_{n-1}]\in H_{n-1}(\Delta^{n-1},\partial \Delta^{n-1})$，根据归纳根据前面两个映射是同构，若 $[i_{n-1}]$ 是生成元，$[i_n]$ 也需要是生成元。

25. 胞腔复形

同调群的计算

回忆：球面同调群的生成元

$i_n: \Delta^n \to \Delta^n$ 是恒等映射

$[i_n] \in H_n(\Delta^n, \partial \Delta^n) = H_n(D^n, \partial D^n) \cong \mathbb{Z}$ 是它的生成元。

给定两个 $n$-单形 $\Delta_1^n, \Delta_2^n$，沿着它们俩所有的 $n-1$ 维的面对应粘起来，粘的时候保持顶点的顺序。

那么粘完后会得到一个球面 $S^n$。

那么 $id_{\Delta^n_1} - id_{\Delta^n_2}$ 是一个圈。

我们想要证明 $\tilde H_n(S_n) = \mathbb{Z} \cdot [id_{\Delta^n_1} - id_{\Delta^n_2}]$

$\tilde H_n(S^n) \xrightarrow{\cong} H_n(S^n, \Delta_2^n)$，这个同构源自于一个 $(S^n, \Delta^n_2)$ 长正合列

$H_n(\Delta_1^n, \partial \Delta^n_1) \xrightarrow{\cong} H_n(S^n, \Delta^n_2)$

$H_n(S^n, \Delta^n_2) = \tilde H_n(S^n/\Delta^n_2)$，$H_n(\Delta^n_1, \partial \Delta^n_1) = \tilde H_n(\Delta^n_1/\partial \Delta^n_1)$，$\Delta_1^n/\partial \Delta^n_1 = S^n$，$S^n / \Delta^n_2 = S^n$

因此就有 $\tilde H_n(S^n/\Delta^n_2) = \tilde H_n(\Delta^n_1/\partial \Delta^n_1)$

根据群同构 $\tilde H_n(S^n) \xrightarrow{\cong} H_n(S^n, \Delta_2^n) \xleftarrow{\cong} H_n(\Delta_1^n, \partial \Delta^n_1)$，就有生成元映射到生成元：$[id_{\Delta^n_1} - id_{\Delta^n_2}] \to [id_{\Delta^n_1}] \leftarrow [id_{\Delta^n_1}]$

因此我们就证明了 $\tilde H_n(S^n) \cong \mathbb{Z} \cdot [id_{\Delta^n_1} - id_{\Delta^n_2}]$

映射度理论 (Degree)

定义

令 $f: S^n \to S^n$，$H_n(S^n) = \mathbb{Z} \cdot \alpha$

就有一个诱导的群同态 $f_\star : H_n(S^n) \to H_n(S^n)$，$f_\star(\alpha) = d \cdot \alpha$ 对某个 $d \in \mathbb{Z}$

我们就把 $d$ 这个整数叫做映射 $f$ 的 映射度 (degree)，记作 $\deg f = d$
基本性质
- $\deg id_{S^n} = 1$
- 如果 $f: S^n \to S^n$ 不是满射，那么 $\deg f = 0$。
  
  证明：存在点 $p \in S^n$ 使得 $f(S^n) \subset S^n/\set{p}$。根据球极投影 $S^n / \set{p} = \mathbb{R}^n$，因为 $\mathbb{R}^n$ 是凸集，所以 $S^n/\set{p}$ 是可缩的，那么就有 $H_n(S^n / \set{p}) = 0$。我们将 $f$ 分解为 $f: S^n \to S^n/\set{p} \hookrightarrow S^n$，那么也可以将 $f_\star$ 分解为 $f_\star: H_n(S^n) = H_n(S^n/\set{p}) \to H_n(S^n)$。因为中间的 $H_n(S^n /\set{p}) = 0$，就有 $f_\star = 0$。因此 $\deg f = 0$。
- 如果 $f \simeq g$，那么 $f_\star = g_\star$，进一步的 $\deg f = \deg g$。
- $(fg)_\star = f_\star g_\star$，因此 $\deg (f \circ g) = \deg f \cdot \deg g$
- 假设 $f: S^n \to S^n$ 是一个同伦等价，那么存在 $g: S^n \to S^n$ 使得 $f \circ g \simeq id_{S^n}, g \circ f \simeq id_{S^n}$。根据上面的第 3、4 条，$\deg f \deg g = \deg (f \circ g) = \deg id_{S^n} = 1$。因此 $\deg f = \pm 1$。
镜面反射的映射度

令 $S^n = \set{(x_1, x_2, \cdots, x_{n+1}) \in \mathbb{R}^{n+1} \mid x_1^n + \cdots + x_{n+1}^2 = 1}$。

考虑 $f_i: S^n \to S^n$ 是一个沿着 $i$-轴的镜面反射，$f(x_1, \cdots, x_n) = (x_1, \cdots, x_{i-1}, -x_i, x_{i+1}, \cdots, x_{n+1})$

则 $\deg f_i = -1$。

证明 :

把两个 $n$-单形沿着它们所有 $n-1$ 维的面对应粘起来，保持顶点的顺序，得到 $S^n$。

根据上面的例子 $[id_{\Delta^n_1} - id_{\Delta^n_2}]$ 是 $H_n(S^n)$ 的生成元。

如果让 $i-$ 轴如图，那么镜面反射就有 $f_{i\star}[id_{\Delta^n_1} - id_{\Delta^n_2}] = [id_{\Delta^n_2} - id_{\Delta^n_1}]$。

因此 $\deg f_i = -1$。
对径映射的映射度

令 $f: S^n \to S^n$，$f(x) = -x$，则 $\deg f = (-1)^{n+1}$。

证明：

$f = f_1 \circ f_2 \circ \cdots \circ f_{n+1}$，其中 $f_i(x_1, \cdots, x_{n+1}) = (x_1, \cdots, x_{i-1}, -x_i, x_{i+1} \cdots x_{n+1})$。

那么 $\deg f = \deg f_1 \cdot \cdots \cdot \deg f_{n+1} = (-1)^{n+1}$。
没有不动点的映射的映射度

令 $f: S^n \to S^n$ 没有不动点，即 $\forall x \in S^n, f(x) \neq x$。

则 $\deg f = (-1)^{n+1}$。

证明：

如果 $f(x) \neq x$，考虑线段 $(1-t)f(x) - tx$，则这个线段不通过原点（球心）。

则 $|(1-t) f(x) - tx| \neq 0, \forall t$。

因此可以构造 $F: S^n \times I \to S^n$，$F(x, t) = \frac{(1-t)f(x) - tx}{|(1-t)f(x) - tx|}$ 良定义。其中 $F(x, 0) = f(x)$，$F(x, 1) = -x$。

则 $f \simeq -id_{S^n}$（对径映射）。

因此 $\deg f = \deg -id_{S^n} = (-1)^{n+1}$。
唯一能自由作用于偶数维球面的群是二元群

令 $n$ 是偶数。二元群 $\mathbb{Z}_2$ 是唯一的一个非平凡群使得这个群可以自由地作用在 $S^n$ 上。
- 回忆：自由群作用
  $G \curvearrowright S^n$，对任意 $e \neq g \in G$，都有 $g \cdot x \neq x, \forall x \in S^n$（除了恒等元都不会作用出不动点）。
证明：

令 $G \curvearrowright S^n$ 是一个自由的群作用，对 $\forall g \in G$，$g: S^n \to S^n$，$x \to g \cdot x$ 是一个同胚。则 $\deg g = \pm 1$

定义 $d: G \to \mathbb{Z}_2 = \set{\pm 1}$，$d(g) = \deg g$。

因为 $d(g_1 g_2) = \deg(g_1 g_2) = \deg g_1 \deg g_2 = d(g_1) d(g_2)$，所以 $d$ 是一个群同态。

如果 $g \neq e$，映射 $g: S^n \to S^n$ 没有不动点，因此 $\deg g = (-1)^{n+1}$。因为 $n$ 是偶数，所以 $\deg g = 1$。

故 $\ker d = \set{e}$，这就意味着 $d$ 是一个单射。因此 $G = \set{e} \text{ or } \mathbb{Z}_2$。
只有奇数维球面才有连续切向量场

$S^n$ 有一个连续的、处处非零的切向量场 $\Leftrightarrow$ $n$ 是奇数。

证明：

"$\Leftarrow$":

令 $n = 2k - 1$，定义 $v(x_1, x_2, \cdots, x_{2k-1}, x_{2k}) = (-x_2, x_1, \cdots, -x_{2k}, x_{2k-1})$，其中 $(x_1, \cdots, x_{2k}) \in S^n$，那么就有 $v(x) \bot x$（做点积等于 $0$）。

因此 $v(x)$ 确实是一个连续的切向量场，且 $|v(x)| = 1 \neq 0$。

"$\Rightarrow$":

令 $v(x)$ 是 $S^n$ 的一个切向量场，使得 $v(x) \neq 0, \forall x \in S^n$。

考虑变换 $\frac{v(x)}{|v(x)|}$，则它也是一个连续的向量场，且 $|\frac{v(x)}{|v(x)|}| = 1$。

因此，我们可以一开始就假设向量场 $v(x)$ 满足 $|v(x)| = 1$。

令 $F: S^n \times I \to S^n$，$F(x, t) = (\cos \pi t)x + (\sin \pi t) v(x)$

备注：$x+v(x)$ 连接后构成一个平面，这个平面和 $S^n$ 交成一个大圆，$F(x, t)$ 就是在这个大圆里转圈，从 $x$ 出发沿着 $v(x)$ 的方向转到 $-x$）

则 $F(x, 0) = x$，$F(x, 1) = -x$。故 $F$ 是 $x$ 到 $-x$ 的同伦。

因此 $\deg id_{S^n} = \deg (-id_{S^n})$，即 $1 = (-1)^{n+1}$，因此 $n$ 是奇数。

胞腔复形 (CW Complex / Cell Complex)

Reference: Hatcher Appendix

定义：胞腔复形 (CW Complex / Cell Complex)

一个拓扑空间 $X$ 被称为 胞腔复形 (CW complex / cell complex)，如果它可以用如下的方式来构造：
1. 令 $X^0$ 是一些点的不交并。这些点被看作是 $0$ 维的胞腔 ($0$-cell)。
2. 假设我们已经构造好了 $X^{n-1}$。我们用如下方式构造 $X^n$：
  
  令 $\set{D^n_\alpha}_{\alpha \in I}$ 是一族 $n$ 维的球。令 $\varphi_\alpha: \partial D_\alpha^n(=S^{n-1}) \to X^{n-1}$ 的连续映射。
  
  令 $X^n$ 是 $X^{n-1} \bigsqcup (\bigsqcup_{\alpha \in I} D_\alpha^n)$ 的粘合空间，通过粘合 $x$ 和 $\varphi_\alpha(x)$，$\forall x \in \partial D_\alpha^n$。
  
  将 $X^n$ 称为一个 $n$ 维的骨架 ($n$-skeleton)。
  
  作为一个集合，$X^n = X^{n-1} \bigsqcup \left(\sqcup_{\alpha \in I} e_\alpha^n\right)$，其中 $e_\alpha^n$ 是一个 $n$ 维的开球，称为 $n$ 维的胞腔 ($n$-cell)。
3. 如果上述的构造过程在某一个有限的 $n$ 停止，就令 $X = X^n$。将这个 $X$ 称为一个 $n$ 维的胞腔复形 ($n$-dimensional CW Complex)。
  
  另一种情况，如果没有在有限步停止，就令 $X = \bigcup_{n = 0}^{\infty} X^n$，在这个 $X$ 上装备一个拓扑（这个拓扑称为弱拓扑 (weak topology)）：$A \subseteq X$ 是开的当且仅当对于 $\forall n$ 都有 $A \cap X^n$ 是开的。
- 特征映射 (Characteristic Map)
  
  令 $e_\alpha^n$ 是胞腔复形 $X$ 中的一个 $n$ 维的胞腔，则有一个特征映射 (characteristic map) $\Phi_\alpha: D_\alpha^n \to X$，$\Phi_\alpha|_{\partial D_\alpha^n} = \varphi_\alpha$。
  
  $\Phi_\alpha$ 通过下面的复合映射定义：
  
  $\Phi_\alpha: D_\alpha^n \hookrightarrow X^{n-1} \bigsqcup \left(\sqcup_\alpha D_\alpha^n \right) \xrightarrow{\text{Identification map}} X^n \hookrightarrow X$
- 子复形 (Subcomplex)
  
  考虑子空间 $A \subset X$，$A$ 被称为一个 子复形 (subcomplex)，如果 $A$ 是闭集，且 $A$ 是一些 $X$ 中胞腔的并。
  
  证明 $A$ 是一个胞腔复形：
  
  如果 $e_\alpha^n \subset A$，则 $\Phi_\alpha(D_\alpha^n) \subset A$。因为 $A$ 是闭集，所以 $\Phi_\alpha(\partial D_\alpha^n) = \varphi_\alpha(\partial D_\alpha^n) \subset A$。
  
  则 $A$ 确实是一个胞腔复形。
  
  将 $(X, A)$ 称为一个 胞腔对 (CW pair)。
胞腔复形的性质
- 胞腔复形中的紧集只能与有限多个胞腔相交
  
  若 $C \subset X$ 是一个紧子集，则 $C$ 只能和有限多个胞腔相交。
  
  (Hatcher prop. A.1)
- 推论：每个胞腔的闭包只能与有限多个胞腔相交
  
  每一个胞腔的闭包只能和有限多个胞腔相交。
  
  证明：
  
  对一个胞腔 $e_\alpha^n$，$\overline{e_\alpha^n} = \Phi_\alpha(D_\alpha^n)$，因为 $D_\alpha^n$ 是紧的，所以 $\Phi_\alpha(D_\alpha^n)$ 也是紧的。
- 子复形是好对
  
  对子复形 $A \subset X$，则 $(X, A)$ 是一个好对 (Good Pair)。
  
  (Hatcher prop. A.5)

26. 胞腔同调群

胞腔复形

回忆：胞腔复形
1. 设 $X^0$ 是一些点的不交并，这些点被称为 $0$-Cell，即 $0$ 维的胞腔；
1. 假设我们构造好了 $X^{n-1}$，则令 $X^n=X^{n-1}\sqcup_\alpha D_\alpha^n/(x\sim \varphi_\alpha(x),\forall x\in \partial D_\alpha^n)$，其中 $\varphi_\alpha:S^{n-1}\to X^{n-1}$ 为 attaching map.
2. 如果在有限 $n$ 停止，令 $X=X^n$，如果无穷维，则令 $X = \bigcup_{n = 0}^{\infin} X^n$，在这个 $X$ 上装备一个拓扑（这个拓扑称为弱拓扑 (weak topology)）：$A \subseteq X$ 是开的当且仅当对于 $\forall n$ 都有 $A \cap X^n$ 是开的。
回忆：特征映射 (Characteristic Map)

$\Phi_\alpha:D_\alpha^n\hookrightarrow X^{n-1}\sqcup_\alpha D_\alpha^n\to X^n\hookrightarrow X$.
- 例子：$n$ 维球面
  
  $S^n$ 为 $n$ 维球面，有 $S^n=e^0\cup e^n$，这是说胞腔复形首先由一个零维点为起点，在 $1$ 到 $n-1$ 维不加入任何东西，在 $n$ 维加上一个 $D^n$，其中粘合映射 $\varphi:\partial S^n=S^{n-1}\to X^{n-1}=e^0$（把球的边界粘合为一点）
  
  如果用二维情形理解，就是说将圆形边界粘合为一点可以得到 $2$ 维球面。
- 例子：Torus
  
  想象将环面按照 $a$ 和 $b$ 这两圈剪开，得到右边的矩形，矩形的四个顶点都是环面上的同一个点 $v$。
  
  因此，环面可以看成是一个零维的起点 $v$，在一维扩展出两个圈 $a$ 以及 $b$，并在二维扩展出一个矩形并将边界粘合到 $a,b$ 上形成的胞腔复形。
  
  $X^0=\set{v}$，$X^1=S^1\vee S^1$，$X^2=X$；
- 例子：亏格为 $g$ 的曲面
  
  对于亏格为 $g$ 的曲面，它也可以看成是一个零维的起点 $v$，在一维扩展出 $2g$ 个圈 $A_1,\cdots, A_g,B_1,\cdots,B_g$，随后再在二维扩展出一个圆（$2g$ 边形）并与边界粘合后形成的胞腔复形（回忆：亏格为 $g$ 曲面的粘合）
- 例子：$n$ 维实射影空间
  
  $X=\mathbb{R}{\rm P}^n$，我们曾经粘合通过原点的直线来构造它，或者粘合 $S^{n}$ 的对径点来构造它，或者粘合 $D^{n}$ 边界的对径点来构造它。
  
  注意到 $D^n$ 的边界是 $S^{n-1}$，这意味着从 $D^n$ 的边界上看我们拿到的是 $\mathbb{R}{\rm P}^{n-1}$.
  
  于是从胞腔复形的角度来看，我们构造 $\mathbb{R}{\rm P}^{n}$ 的方式就是：$\mathbb{R}{\rm P}^{n-1}\cup e^n$，其中 $\varphi:\partial D^n= S^{n-1}\to X^{n-1}=\mathbb{R}\text{P}^{n-1}=e^0\cup e^1\cup\cdots\cup e^n$.
- 例子：$n$ 维复射影空间
  
  类似实射影空间，我们有 $X=e^0\cup e^2\cup\cdots\cup e^{2n}$.
引理：Hatcher 2.3.4

$X$ 是一个 CW 复形，则：
1. $H_k(X^n,X^{n-1})=\begin{cases}\text{以 } n-\text{cell 为基的自由 Abel 群}&k=n\\0&\text{其他}\end{cases}$.
2. $H_k(X^n)=0,k>n$.
3. 考察从 $i_n:X_n\hookrightarrow X$ 嵌入，则 $H_k(X_n)\xrightarrow{\cong} H_k(X),\forall k<n$.
证明：
1. $\set{e_\alpha^n}_{\alpha\in I}$ 是 $X$ 的所有 $n$-Cell，则 $X^n/X^{n-1}\simeq \bigvee_{\alpha\in I} D_\alpha^n/\partial D_\alpha^n=\bigvee_{\alpha\in I}S_\alpha^n$
于是 $H_k(X^n,X^{n-1})=\tilde H_k(X^n/X^{n-1})=\tilde H_k(\bigvee_{\alpha\in I} S_\alpha)=\bigoplus_{\alpha\in I}\tilde H_k(S_\alpha^n)$.

根据球面的同调群得到结论。
1. 对 $(X^n,X^{n-1})$，考察长正合列 $\to H_{k+1}(X^n,X^{n-1})\to H_{k}(X^{n-1})\to H_k(X^{n})\to H_k(X^n,X^{n-1})\to\cdots$
当 $k>n$，我们有 $H_k(X^n,X^{n-1})=H_{k+1}(X^n,X^{n-1})=1$，于是 $H_k(X^{n-1})\cong H_k(X^n)$.

对 $(X^{n-1},X^{n-2})$，于是有 $H_k(X^{n-2})\cong H_k(X^{n-1})$，以此类推，我们有 $H_k(X^n)=H_k(X^0)=0$.
1. 如果 $k\leq n-1$，我们有 $H_k(X^n)\cong H_k(X^{n+1})$，以此类推有 $H_k(X^n)\cong H_k(X^N)=H_k(X)$，因而嵌入映射诱导出的是同构。（$X$ 是有限维）
如果 $X$ 是无限维，我们证明映射是满射且单射。

满射：考察 $[z]\in H_k(X)$，$z=\sum n_i \sigma_i$，一个有限和，结论为 $\bigcup_{i} \text{Im}(\sigma_i)\in X^m$，对于某 $m>n$. 由于 $[z]\in H_k(X^m)\cong H_k(X^n)$，于是 $H_k(X_n)\to H_k(X)$ 是满射。

单射：”用同样的论证可以得到“，我的建议是翻看 Hatcher 书。
例子：”绕 $n$ 次圈“的映射的映射度

考察 $f:S^1\to S^1$，其中 $z\to z^n,n\geq 0$. 我们有 $\deg f=n$.

形式上将，这是把圆切成 $n$ 等份，其中 $[e_1+e_2+\cdots+e_n]\in H_1(S^1)$ 是生成元：

注意到 $f$ 将这个生成元映射为 $n[e]$，自然 $\deg f=n$.
例子：$n$ 维球面

如图，$\Delta_1^n$ 和 $\Delta_2^n$ 是 $n$ 维复形，分别对应上下半球面，其中 $[\Delta_1^n-\Delta_2^n]$ 是 $H_n(S^n)$ 的生成元。

（回忆上节课的内容）

胞腔链复形 (Cellular Chain Complex)

如图所示，对于相对同调群，我们可以画出图上所示图表。

根据刚才的引理，我们还可以在图中圈出为 $0$ 的项：

图中，$d_{n+1}=j_n\circ \partial_{n+1}$，$d_{n}=j_{n-1}\circ \partial_n$.

于是 $d_n\circ d_{n+1}=j_{n-1}\circ\partial_n\circ j_{n}\circ\partial_{n+1}=0$.

于是中间的 $(*)$ 确实是一个链复形，我们称之为胞腔链复形 (Cellular Chain Complex).

其中 $H_n^{CW}(X)=$ 图中的第 $n$ 个同调群。

定理

$H_n(X)\cong H_n^{CW}(X)$.

证明：

$H_n(X)\cong H_n(X^{n+1})$，这由先前的引理 (c) 给出.

还有 $H_n(X^{n+1})\cong H_n(X^n)/\text{Im}\partial_{n+1}$.

$H_n^{CW}(X)$ 由定义即为 $\ker d_n/\text{Im} d_{n+1}$，由于 $j_n$ 嵌入是单射，于是 $\text{Im} \partial_{n+1}\cong \text{Im} d_{n+1}$（$d_{n+1}=j_n\circ \partial_{n+1}$）

由 $j_{n-1}$ 嵌入是单射，于是 $\ker d_n=\ker \partial_n$.（$d_n=j_{n-1}\circ \partial_n$）

另一方面，还因为正合列，因此 $\ker \partial_n= \text{Im} j_n\cong H_n(X^n)$，因此原式等于 $H_n(X)$.
- 注
  1. $H_n(X)=0$ 若 $X$ 没有 $n$-Cell（由上面的定理立得）；例如球面的同调群，除了 $H_0$ 与 $H_n$ 之外的同调群为 $0$。
  2. 若 $X$ 没有相邻维的 Cell（若在 $n$ 维上有 Cell，则 $n-1,n+1$ 维上没有 Cell），则 $H_n(X)\cong\bigoplus_{\alpha\in I}e_\alpha^n$. 例如，对复射影平面 $\mathbb{C}P^n$，则 $H_i(\mathbb{C}P^n)=\begin{cases}\mathbb{Z},2\mid i\\0,2\not\mid i\end{cases}$.
问题：如何计算 $d_n$？

根据定义，有 $j_{0}$ 是一个 identity map，于是有 $d_1:H_1(X^1,X^0)\to H_0(X^0)=\partial_1$，其中 $H_1(X^1,X^0)$ 的某生成元为 $[e_1:(v_0\to v_1)]$，有 $d_1(e_1)=[v_1-v_0]$.

这意味着，如果 $X$ 是连通的，且 $X$ 只有一个 $0$-Cell，则 $d_1=0$.
- 定理：Cellular Boundary Formula
  
  若 $n> 1$，则 $d_n(e_\alpha^n)=\sum_{\beta} d_{\alpha,\beta} e_\beta^{n-1}$，其中 $d_{\alpha,\beta}=\deg \Delta_{\alpha,\beta}$，其中 $\Delta_{\alpha,\beta}:S_\alpha^{n-1}=\partial D_{\alpha}^n\xrightarrow{\varphi_{\alpha}} X^{n-1}\xrightarrow{\text{粘合},\text{将 } X^{n-1}-S_{\beta}^{n-1} \text{粘合为一个点}} S_{\beta}^{n-1}$
  
  注：求和 $\sum_\beta$ 是有限项因为 $\varphi_\alpha$ 只会与有限个 Cell 相交。
  
  证明：
  
  事实上，上述的图表都是交换图表，箭头略去。
  
  其中
  - $\Phi_\alpha$ 是特征映射
  - $q: X^{n-1} \to X^{n-1}/X^{n-2}$ 是 CW 复形构造自然诱导的粘合映射
  - $q_\beta: X^{n-1}/X^{n-2} \to S_{\beta}^{n-1}$ 是粘合映射，将除了 $S_\beta^{n-1}$ 外的点，即 $e^{n-1}_\beta$ 粘合为一点
  - $\Delta_{\alpha, \beta} = q_\beta \circ q \circ \varphi_\alpha$
  - $j_{n-1}: X^{n-1} \hookrightarrow X^{n-1}/X^{n-2}$ 是嵌入映射
  考察 $H_n(D_\alpha^n,\partial D_\alpha^n)$ 的生成元，它是 $[D_\alpha^n]$，有 $\Phi_{\alpha\star}([D_\alpha^n])=[e_\alpha^n]$.
  
  于是 $d_n(e_\alpha^n)=j_{n-1}\circ \varphi_{\alpha\star}\circ \partial [D_\alpha^n]=\sum_\beta d_{\alpha\beta} e_\beta^{n-1}$.
  
  两边复合 $q_{\beta\star}$，则右边只剩下 $d_{\alpha\beta} e_\beta^{n-1}$，左边变为 $q_{\beta\star}\circ j_{n-1}\circ \varphi_{\alpha\star}\circ \partial [D_\alpha^n]$
  
  其中 $q_{\beta\star}\circ j_{n-1}\circ \varphi_{\alpha\star}=\Delta_{\alpha\beta\star}$，于是 $\Delta_{\alpha\beta\star}(e_\alpha^{n-1})=d_{\alpha\beta} e_{\beta}^{n-1}$，于是 $d_{\alpha\beta}=\deg \Delta_{\alpha\beta}$.
例：克莱因瓶

$X=\text{Klein Bottle}$，它可以看成有一个 $0$-Cell，两个 $1$-Cell 及一个 $2$-Cell：

注意到 $d_1=0$，$d_2(e^2)=d_{11}e_1^1+d_{12}e_2^1$，其中 $\Delta_{11}:\partial D^2=S^1\to X^1\to S_1^1$

如图，因此 $\deg \Delta_{11}=0$.

27. 胞腔同调群的计算与 Euler-Poincare 引理

本节涉及：胞腔同调计算的练习（请参考 Wk15 作业）、Mayer-Vietoris sequences 与 Euler-Poincare 引理（可以参考 29 节更强的引理）

28. Borsuk-Ulam 定理

欧拉公式 (Euler's Formula)

回忆

令 $X$ 是多面体，它同胚于亏格为 $g$ 的曲面，则 $\chi(X)=\beta_0-\beta_1+\beta_2=1-2g+1=2-2g$ （$\beta$ - Betti Number，同调群的秩）

另一方面，根据 E-P 定理，这还可以写成 $a_0(X)-a_1(X)+a_2(X)$ （$a_i$: $i$ 维胞腔的个数），也就是 $v-e+f=2-2g$.

如果它是凸多面体，或者它同胚于球面 $S^2$ ，那么就有 $v-e+f=2$.

这回答了我们在第一节课就提出的问题。

（实际上，根据我们切割的方式不同，不同维度的胞腔数量也不同，然而不管我们怎么切割，交错和（欧拉示形数）是一个拓扑不变量）

应用：Borsuk-Ulam 定理

准备工作：同调理论的系数可以换成任意 Abel 群
- 回忆：同调理论的定义
  有一个链复形 $C_n(X)$，群里的元素长成形式和 $\sum_{i} n_i\sigma_i$，其中 $n_i$ 为整数且只有有限个。（这有时也被叫做整系数的同调理论）
我们推广这一定义。固定一个 Abel 群 $G$，令 $C_n(X;G)$ 表示形式和 $\sum_{i} n_i\sigma_i$，其中 $n_i\in G$ 且是有限个（非零项只有有限个）。$\sigma_i$ 是 $n$ 维奇异单形 $\Delta^n\to X$。

事实上，我们曾经建立的所有理论都可以被推广到同调群里。例如取边界 $\partial(\sum_i n_i\sigma_i)=\sum_{i,j}(-1)^j n_i\sigma_i|_{[v_0,\cdots,\tilde v_j,\cdots,v_n]}$

进而我们得到 $\set{C_n(X;G),\partial}_{n\in \mathbb{Z}}$，这是一个链复形。对其取同调群 $H_n(X;G):=H_n(\set{C_n(X;G),\partial}_{n\in \mathbb{Z}})$，称其为系数是 $G$ 的同调群。

我们也可以得到相对同调群 $H_n(X,A;G)$，也可以推出相对同调理论。

类似地，我们还可以得到约化同调理论：$\to C_1(X;G)\xrightarrow{\partial} C_0(X;G)\xrightarrow{\varepsilon} G\to 0$，其中 $\varepsilon(\sum_i n_i\sigma_i)=\sum_i n_i$.

进而可以定义约化同调群 $\tilde H_n(X;G)$.

同样地，对胞腔理论，令 $X$ 是一个 $CW$ 复形，我们可以得到胞腔链复形 $\cdots\to H_n(X^n,X^{n-1};G)\xrightarrow{d_n} H_{n-1}(X^{n-1},X^{n-2};G)\xrightarrow{d_{n-1}}\cdots$

如此我们可以定义胞腔同调群 $H_n^{CW}(X;G):=$ 上面胞腔链复形的同调群。

与之前相同，我们仍然可以推出 $H_n^{CW}(X;G)\cong H_n(X;G)$.
替换系数常见的例子

通常地，我们可以将 $G$ 取 $\mathbb{Z},\mathbb{R},\mathbb{C},\mathbb{Z}_2$ 等等。

练习：映射度的概念也可以推广到一般的群 $G$ 中，即 $f:S^n\to S^n$，映射度为 $d$，那么 $f_\star:\tilde H_n(S^n;G)\to\tilde H_n(S^n;G)$ 会有 $\tilde H_n(S^n;G)\cong G$，且 $f_\star$ 的映射度是由下面的公式给出： $f_\star(g)=dg$. （可以参考 Hatcher 2.49）
例子：取二元群时实射影空间的同调群

令 $G=\mathbb{Z}_2$，我们可以考虑实射影空间 $\mathbb{R}P^n$ 的 CW 同调群。

曾经我们验证过，对于整系数，其 CW 复形形如：

$\cdots\xrightarrow{2} G \xrightarrow{0} G\xrightarrow{2} G\to\cdots\to G\xrightarrow{2} G\xrightarrow{0} G\to 0$

我们令 $G$ 是二元群，表达式就变成了

$\cdots \xrightarrow{0} \mathbb{Z}_2\xrightarrow{0} \mathbb{Z}_2\xrightarrow{0}\cdots\xrightarrow{0} \mathbb{Z}_2\to 0$.

那么这个链复形的同调群就是 $H_k(\mathbb{R}P^n;\mathbb{Z}_2)=\mathbb{Z}_2 ,\forall 0\leq k\leq n$.
Borsuk-Ulam 定理

考虑映射 $g:S^n\to\mathbb{R}^n$ 是连续映射，那么 $\exists x\in S^n$，使得 $g(x)=g(-x)$.

形象地理解，如果我们将球面映射到平面（将球面拍扁），那么一定会有一对对径点被映射到同一个点。

证明：$n=1$ 我们已经证明过了。这是因为，如果我们定义 $f(x)=\cfrac{g(x)-g(-x)}{|g(x)-g(-x)|}$，它的像是 $\set{-1,1}$，这与 $S^1$ 连通矛盾。

因此在证明这个定理时，我们总是假设 $n\geq 2$.
- 引理（奇函数的映射度也是奇数）
  
  考虑映射 $f:S^n\to S^n$，$f(-x)=-f(x)$，$\forall x\in S^n$，那么 $\deg f \text{ is odd}$.
  
  证明：
  
  考虑覆叠映射 $p:S^n\to \mathbb{R}P^n$，这是一个两层的覆叠映射。考虑 $\Delta^k$ 是一个 $k$ 维单形，有 $\Delta^k\xrightarrow{\sigma} \mathbb{R}P^n$.
  
  固定 $x_0$，有 $\sigma(x_0)\in \mathbb{R}P^n$，根据提升判别法，我们有 $\sigma$ 存在两个提升 $\tilde \sigma_1$ 与 $\tilde \sigma_2$（这是因为 $\pi_1(\Delta^k)=\set{e}$，且 $|p^{-1}(\sigma(x_0))|=2$）
  
  考虑 $p_\#: C_k(S^n;\mathbb{Z}_2)\to C_k(\mathbb{R}P^n;\mathbb{Z}_2)$，这个映射一定是满射（这根据提升可以得到）
  
  还可以定义 $\tau:C_k(\mathbb{R}P^n;\mathbb{Z}_2)\to C_k(S^n;\mathbb{Z}_2)$，其中 $\tau(\sigma):=\tilde \sigma_1+\tilde \sigma_2$.
  
  于是我们得到短正合列 $0\to C_k(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow{\tau} C_k(S^n;\mathbb{Z}_2)\xrightarrow p_\# C_k(\mathbb{R}P^n;\mathbb{Z}_2)\to 0$，这是易于验证的，例如对 $p_\# \circ \tau(\sigma)=p_\#(\tilde \sigma_1+\tilde\sigma_2)=2\sigma=0$.
  
  这可以诱导同调群的长正合列：
  
  $0(H_{n+1}(\mathbb{R}P^n;\mathbb{Z}_2))\to H_n(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow{\tau_\star}H_n(S^n;\mathbb{Z}_2)\xrightarrow{p_\star}H_n(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow{\partial} H_{n-1}(\mathbb{R}P^n;\mathbb{Z}_2)\to\cdots$.
  
  取中间的代表项：
  
  $0(H_{n-1}(S^n;\mathbb{Z}_2))\to\cdots\to 0(H_k(S^n;\mathbb{Z}_2))\to H_k(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow{\partial} H_{k-1}(\mathbb{R}P^n;\mathbb{Z}_2)\to 0(H_{k-1}(S^n;\mathbb{Z}_2))$
  
  这个正合列最后的项是
  
  $\to 0\to H_1(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow{\partial} H_0(\mathbb{R}P^n;\mathbb{Z}_2)\to H_0(S^n;\mathbb{Z}_2)\xrightarrow{p_\star} H_0(\mathbb{R}P^n;\mathbb{Z}_2)\to 0$
  
  我们注意到 $H_n(S^n;\mathbb{Z}_2)=\mathbb{Z}_2$，且 $H_n(\mathbb{R}P^n;\mathbb{Z}_2)=\mathbb{Z}_2$，因此在最上面一行的代表中 $\tau_\star$ 是一个同构；
  
  另一方面对于最上面一行，$p_\star=0$，这意味着 $\partial$ 是单射，同时 $\partial$ 左右两侧集合都是 $\mathbb{Z}_2$，这意味着 $\partial$ 是同构。
  
  类似地，对中间一行，由于 $\partial$ 左右两侧都是 $0$，因此 $\partial$ 全都是同构。
  
  对于最下面一行，因为 $H_0(\mathbb{R}P^n;\mathbb{Z}_2)\to H_0(S^n;\mathbb{Z}_2)$ 映射是 $0$ 映射，$\partial$ 仍然是同构；同时也可以借由此导出 $p_\star$ 也是一个同构。
  
  因此我们得到了下面三列：
  
  $0(H_{n+1}(\mathbb{R}P^n;\mathbb{Z}_2))\to H_n(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow[\cong]{\tau_\star}H_n(S^n;\mathbb{Z}_2)\xrightarrow{p_\star=0}H_n(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow[\cong]{\partial} H_{n-1}(\mathbb{R}P^n;\mathbb{Z}_2)\to\cdots$
  
  $0(H_{n-1}(S^n;\mathbb{Z}_2))\to\cdots\to 0(H_k(S^n;\mathbb{Z}_2))\to H_k(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow[\cong]{\partial} H_{k-1}(\mathbb{R}P^n;\mathbb{Z}_2)\to 0(H_{k-1}(S^n;\mathbb{Z}_2))$
  
  $\to 0\to H_1(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow[\cong]{\partial} H_0(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow{0} H_0(S^n;\mathbb{Z}_2)\xrightarrow[\cong]{p_\star} H_0(\mathbb{R}P^n;\mathbb{Z}_2)\to 0$
  
  考察映射 $f:S^n\to S^n$ 有 $f(-x)=-f(x)$，它会诱导一个映射：$\bar f:\mathbb{R}P^n\to\mathbb{R}P^n:\set{x,-x}\to \set{f(x),-f(x)}$，这是良定义的。
  
  于是我们得到下面的交换图表：
  
  “交换”的解释：
  
  右侧：$pf=\bar fp$，因此交换性是自然的。
  
  左侧：
  
  我们有如上的交换图表，因此 $f\circ \tilde \sigma_i$ 是 $f\circ \sigma$ 的提升，因此由 $\tau$ 的定义，左侧的图表是交换的。
  
  根据自然性定理，我们进一步得到长正合列的交换图表：
  
  我们看左边的正方形，由于 $H_0(\mathbb{R}P^n;\mathbb{Z}_2)$ 是道路连通的拓扑空间，右边的那个 $\bar f_\star$ 诱导了一个同构，进而 $\bar f_\star$ 在 $H_1$ 上也是同构。
  
  更多地，我们考察上面的正合列，对 $k$ 做归纳法，我们可以进一步得到 $\bar f_\star$ 在 $H_k(\mathbb{R}P^n;\mathbb{Z}_2)\xrightarrow{\bar f_\star} H_k(\mathbb{R}P^n;\mathbb{Z}_2)$ 上全是同构（$\partial$ 都是同构）。
  
  考察一开始的长正合列：
  
  因此 $f_\star:H_n(S^n;\mathbb{Z}_2)\to H_n(S^n;\mathbb{Z}_2)$ 也诱导了同构。
  
  因此 $f_\star(1)=1$
  
  根据我们此前的练习，我们知道 $f_\star(1)=\deg f\cdot 1$，因此 $\deg f=1\in \mathbb{Z}_2$，这意味着 $\deg f$ 在 $\mathbb{Z}$ 中是奇数。
进而，我们证明主定理：

$g:S^n\to \mathbb{R}^n$ 是一个连续映射，令 $f(x)=g(x)- g(-x)$，则 $f(-x)=-f(x)$。如果 $g(x)\neq g(-x),\forall x\in S^n$，这意味着 $f(x)\neq 0,\forall x\in S^n$。

于是令 $h(x)=\cfrac{f(x)}{|f(x)|}$，则 $h(-x)=-h(x)$ 且 $h:S^n\to S^{n-1}$.

考虑如图所示限制，有 $h|_{S^{n-1}}:S^{n-1}\to S^{n-1}$，根据引理，有 $\deg(h|_{S^{n-1}})$ 是奇数。

然而，考虑嵌入映射 $S^{n-1}\hookrightarrow S^n\xrightarrow{h} S^{n-1}$，其中 $h|_{S^{n-1}}= h\circ i$.

考察嵌入映射诱导的同调群：$H_{n-1}(S^{n-1})\xrightarrow{i_\star} H_{n-1}(S^n)\xrightarrow{h_\star} H_{n-1}(S^{n-1})$.

由于 $H_{n-1}(S^n)=0$，我们得到 $h|_{S^{n-1}\star}=0$，因此 $\deg (h|_{S^{n-1}})=0$，矛盾。

这意味着 $\exists x$，使得 $g(x)=g(-x)$.
推论

考虑 $A_1,\cdots,A_{n+1}$ 是 $S^n$ 中的 $n+1$ 个闭集且 $S^n$ 可以被这 $n+1$ 个闭集覆盖，即 $S=\cup_i A_i$.

那么 $\exists k$ 以及 $y\in S^n$，使得 $A_k$ 同时包含 $y$ 和 $-y$.

证明：

定义映射 $f:S^n\to \mathbb{R}^n$，其中 $f(x):=(d(x,A_1),d(x,A_2),\cdots,d(x,A_n))$，那么 $f$ 是一个连续函数。

这意味着 $\exists y\in S^n$，使得 $f(y)=f(-y)$. 这就是说 $d(y,A_k)=d(-y,A_k),\forall 1\leq k\leq n$.

如果 $d(y,A_k)>0$，这意味着 $y,-y\in A_{n+1}$；

否则，$\exists k$，使得 $d(y,A_k)=d(-y,A_k)=0$，即 $y,-y\in A_k$ （$A_k$ 是闭集，因此包含了所有距离为 $0$ 的点）

应用：Lefschetz 不动点定理

定义：有限单纯复形（Finite Simplicial Complex）

一个集族 $K$ 包含有限多个落在 $\mathbb{R}^N$ 中的单形称之为有限单纯复形 (finite simplicial complex)如果：(1) 若某一个单形落在了集族中，那么它的每一个面也都落在了集族中；(2) 若两个单形相交，则它们相交的部分必须是它们的一个公共面。

我们记 $|K|$ 表示它里面所有的单形并起来，则 $|K|\subset \mathbb{R}^N$.

那么 $\mathbb{R}^N$ 上的度量诱导了 $|K|$ 的度量，这使得 $|K|$ 成为 $\mathbb{R}^N$ 的子空间，并且 $|K|$ 是一个紧空间。

由此我们定义三角剖分 (Triangulation)：

给定一个拓扑空间 $X$，$X$ 上的一个三角剖分说的是选择一个同胚 $h:|K|\xrightarrow{\cong} X$。

例如：

注：有限单纯复形是 CW 复形的特殊情况，即 $\set{\text{有限单纯复形}}\subset \set{\text{CW 复形}}$.

取单形的内部，其对应的概念就是 CW 复形的胞腔。

29. Lefschetz 不动点定理

应用：Lefschetz 不动点定理

定理：Lefschetz 不动点定理

设 $K$ 是一个 $n$ 维的单纯复形，令 $f: |K| \to |K|$ 连续。则 $f_\star: H_k(|K|, \mathbb{Q}) \to H_k(|K|, \mathbb{Q})$ 是一个 $\mathbb{Q}$ 上的线性映射。

令 $\Lambda_f := \sum_{k = 0}^n (-1)^k \text{tr}(f_\star: H_k(|K|, \mathbb{Q}) \to H_k(|K|, \mathbb{Q}))$，其中 $\text{tr}$ 是迹 (trace)。$\Lambda_f$ 称为 $f$ 的 Lefschetz 数 (Lefschetz Number)。（trace 是取一个 $|K|$ 的基，然后计算映射后对角和）

Lefschetz 不动点定理：如果 $\Lambda_f \neq 0$，则 $f$ 有不动点。

令 $A = [v_0, \cdots, v_k]$ 是一个 $k$-单形，则 $\hat A = \frac{1}{k+1}(v_0+\cdots+v_k)$ 称为 $A$ 的重心 (barycenter)。

令 $K$ 是一个有限的单纯复形，且想要构造一个新的单纯复形 $K^{(1)}$ 通过重心重分 (barycenter subdivision)

操作方法：

$K^{(1)}$ 中的顶点是 $K$ 中所有单形的重心。

其中的一些重心 $\hat A_0, \cdots, \hat A_k$ 形成了 $K^{(1)}$ 中的某一个单形的顶点，当且仅当存在一个置换 $\sigma$ 使得 $A_{\sigma(0)} \subsetneqq A_{\sigma(1)} \subsetneqq \cdots \subsetneqq A_{\sigma(k)}$，其中 $\hat A_i$ 是 $A_i$ 的重心。

显然有 $|K^{(1)}| = |K|$。

令 $K^{(m)} := (K^{(m-1)})^{(1)}$，也就是上一次的结果再做一次重心重分，即 $m$ 次重心重分的结果。
单纯估计 (Simplicial Approximation)
- 单纯映射 (Simplicial Map)
  
  令 $K$ 和 $L$ 是两个有限的单纯复形。连续映射 $s:|K| \to |L|$ 被称为单纯的 (simplicial)，当它将 $K$ 中的单形线性映射到 $L$ 中的单形，这就意味着如果 $A = [v_0, \cdots, v_k]$ 是 $K$ 中的单形，则 $s(A)$ 也是 $L$ 中的单形，且对于 $A$ 中的一个点 $\sum_i t_i v_i$ 有 $s(\sum_i t_i v_i) = \sum_i t_i s(v_i)$，其中 $\set{t_i}$ 是重心坐标，也就是说 $\sum_i t_i = 1, t_i \geqslant 0$。
- 承载子 (Carrier)
  
  对于 $f: |K| \to |L|$ 是连续映射，则对 $\forall x \in |K|$，点 $f(x)$ 落在 $L$ 中唯一的一个单形的内部。我们将这个唯一的单形称为 $f(x)$ 的承载子 (Carrier)。
一个单纯映射 $s: |K| \to |L|$ 被称为一个连续映射 $f: |K| \to |L|$ 的单纯估计 (simplicial approximation)，当对 $\forall x \in |K|$ 都有 $s(x)$ 落在 $f(x)$ 的承载子中。（也就是说 $s$ 和 $f$ 之间差的不远）
- 注：单纯估计是同伦的
  $s \simeq f$：令 $|L| \subset \mathbb{R}^N$，令 $F(x, t) = (1-t) s(x) + t f(x)$，因为 $s(x)$ 和 $f(x)$ 落在了 $L$ 中同一个单形内，且 $\mathbb{R}^N$ 中的单形是凸集，所以 $F(x, t) \in |L|$，因此 $F$ 良定义。
单纯估计在充分多次重心重分后存在

任取一个 $f:|K| \to |L|$ 是连续映射，如果 $m$ 是一个足够大的数，则存在一个 $s: |K^{(m)}| \to |L|$ 它是 $f: |K^{(m)}| \to |L|$ 的单纯估计。

对这个定理感兴趣，可以看 Armstrong: Section 6.3 的证明。
Hopf Trace Theorem

设 $f: |K| \to |K|$ 满足 $f(|K|^k) \subset |K|^k$，其中 $|K|^k$ 是 $K$ 的 $k$ 维骨架，即所有小于等于 $k$ 维单形的并。（将这个条件记为 $(\star)$）

则我们可以推出下面这个交换图表：

如果 $K$ 是一个有限的 $n$ 维单纯复形。设 $f: |K| \to |K|$ 满足 $(\star)$ 条件。

则 $\sum_{k = 0}^n (-1)^k \text{tr}(f_\star: H_k(|K|^k, |K|^{k-1}; \mathbb{Q})) = \sum_{k = 0}^n (-1)^k \text{tr}(f_\star: H_k(|K|; \mathbb{Q}) \to H_k(|K|; \mathbb{Q})) = \Lambda_f$

（这里 $f_\star: H_k(|K|^k, |K|^{k-1}; \mathbb{Q})$ 是 $f_\star: H_k(|K|^k, |K|^{k-1}; \mathbb{Q}) \to H_k(|K|^k, |K|^{k-1}; \mathbb{Q})$ 的简写）
- 注：$f$ 是恒等映射时就是之前的 E-P 引理
  
  当 $f = id_{|K|}$ 时，$LHS = \sum_{k=0}^n (-1)^ka_k(|K|)$，其中 $a_k$ 是 $|K|$ 中 $k$ 维胞腔的个数；$RHS = \chi(|K|)$。
  
  这就意味着 Hopf trace 定理可以推出 Euler-Poincare 定理。
- 引理
  
  令 $V, V_1, V_2$ 是有限维的线性空间，有如下交换图表：
  
  其中 $f, g, h$ 是线性映射，上下两行是正合列，则 $\text{tr}(f) = \text{tr}(g) + \text{tr}(h)$。
下面我们用引理完成对该定理的证明。我们有如下交换图表：

根据上面的引理，有 $\text{tr}(f_\star: H_k(|K|^k, |K|^{k-1}; \mathbb{Q})) = \text{tr} (f_\star: \ker d_k) + \text{tr} (f_\star: \text{Im} d_k)$。

等式两边同时取交错和，则有 $\sum_{k=0}^n(-1)^k \text{tr}(f_\star: H_k(|K|^k, |K|^{k-1}; \mathbb{Q})) = \sum_{k = 0}^n (-1)^k \text{tr}(f_\star: \ker d_k) + \sum_{k = 0}^n (-1)^k \text{tr}(f_\star: \text{Im} d_k) \ \ (\star_1)$

因为 $\text{Im} d_0 = 0$，所以 $\sum_{k = 0}^n (-1)^k \text{tr}(f_\star: \text{Im} d_k) = \sum_{k = 1}^n (-1)^k \text{tr}(f_\star: \text{Im} d_k)$。

依然根据上面的引理，有 $\text{tr}(f_\star: H_k(|K|; \mathbb{Q})) = \text{tr}(f_\star: \ker d_k) + \text{tr}(f_\star : \text{Im} d_{k+1})$。

同样对等式两边取交错和，有 $\sum_{k = 0}^n (-1)^k \text{tr}(f_\star: H_k(|K|; \mathbb{Q})) = \sum_{k = 0}^n (-1)^k \text{tr}(f_\star: \ker d_k) + \sum_{k = 0}^n (-1)^{k+1} \text{tr}(f_\star: \text{Im} d_{k+1}) \ \ (\star_2)$。

因为 $Im d_{n+1} = 0$，则 $\sum_{k = 0}^n (-1)^{k+1} \text{tr}(f_\star: \text{Im} d_{k+1}) = \sum_{k = 0}^{n-1} (-1)^{k+1} \text{tr}(f_\star: \text{Im} d_{k+1}) = \sum_{k = 1}^n (-1)^k \text{tr}(f_\star: \text{Im} d_k)$。

因此，我们发现 $(\star_1)$ 和 $(\star_2)$ 两个等式的右边相等，所以两个左边也相等，即 $\sum_{k=0}^n(-1)^k \text{tr}(f_\star: H_k(|K|^k, |K|^{k-1}; \mathbb{Q})) = \sum_{k = 0}^n (-1)^k \text{tr}(f_\star: H_k(|K|; \mathbb{Q}))$。
证明 Lefschetz 不动点定理

考虑一个连续映射 $f:|K|\to |K|$，考虑原命题的逆否命题：假设 $f$ 没有不动点，则 $\Lambda_f=0$.

证明：

将 $|K|$ 嵌入 $\mathbb{R}^N$，令 $d$ 是由嵌入诱导出的 $K$ 上度量。

令 $g(x)=d(x,f(x))$，则因为 $f(x) \neq x$ $g(x) > 0$。并且因为 $|K|$ 是紧空间，所以 $\exists \varepsilon$ 使得 $g(x) > \varepsilon, \forall x \in |K|$。

由重心重分，我们总可以假设 $K$ 中单形的直径小于 $\frac{\varepsilon}{3}$。

考虑 $s: |K^{(m)}| \to |K|$ 是 $f: |K^{(m)}| \to |K|$ 的单纯估计，其中 $m$ 是足够大的数。因此有 $s \simeq f$，则 $\Lambda_s = \Lambda_f$。（同伦不变量）

对 $\forall \sigma$ 是 $K^{(m)}$ 的一个单形，那么 $s(\sigma)$ 是 $K$ 中的单形。

假设 $\sigma \cap s(\sigma) \neq \varnothing$，令 $x \in \sigma \cap s(\sigma)$，则 $s(x) \in s(\sigma)$。同时，因为 $s(x)$ 落在 $f(x)$ 的承载子 $\tau$ 中（$\tau$ 是单形）。

根据三角不等式 $d(x, f(x)) \leqslant d(x, s(x)) + d(s(x), f(x))$，因为 $x, s(x) \in s(\sigma)$，$s(x), f(x) \in \tau$。而 $K$ 中单形 $s(\sigma), \tau$ 的直径小于 $\frac{\varepsilon}{3}$，所以 $d(x, f(x)) \leqslant \frac{2\varepsilon}{3}$，这与 $g(x) > \varepsilon$ 矛盾。

因此 $\forall \sigma \in K^{(m)}$，$s(\sigma) \cap \sigma = \varnothing$。

因为 $s$ 是单纯映射，$s: (|K^{(m)}|^k, |K^{(m)}|^{k-1}) \to (|K|^k, |K|^{k-1}) \hookrightarrow (|K^{(m)}|^k, |K^{(m)}|^{k-1})$（$s$ 是将单形线性映射到单形，单形的数量只会变少不会变多）

可以参考下图这个例子：

$s_\star: H_k(|K^{(m)}|^k, |K^{(m)}|^{k-1}; \mathbb{Q}) \to H_k(|K^{(m)}|^k, |K^{(m)}|^{k-1}; \mathbb{Q})$。其中 $H_k(|K^{(m)}|^k, |K^{(m)}|^{k-1}; \mathbb{Q}) = \bigoplus_{K^{(m)} \text{中所有} k \text{维单形} \sigma} \mathbb{Q}\sigma$。

令 $s_\star(\sigma) = \sum_i n_i \tau_i$，其中 $\set{\tau_i\mid i\in I}$ 是 $K^{(m)}$ 中所有 $k$ 维单形。

如果 $\dim s(\sigma) < k$，则 $s_\star(\sigma) = 0$。

如果 $\dim s(\sigma) = k$，则 $n_i = \pm 1$ 如果 $\tau_i \subset s(\sigma)$；$n_i = 0$ 如果 $\tau_i \not\subset s(\sigma)$。

因为 $\sigma \cap s(\sigma) = \varnothing, \forall \sigma$，即 $\sigma \not\subset s(\sigma)$，所以 $s(\sigma)$ 中 $\sigma$ 前的系数永远是 $0$。因此 $\text{tr}(s_\star) = 0$。

由 Hopf trace 定理，所以 $\Lambda_s = 0 = \Lambda_f$。
推论

复形 $|K|$ 如果满足 $H_k(|K|; \mathbb{Q}) = \begin{cases} \mathbb{Q} & k = 0 \\ 0 & k \neq 0\end{cases}$

对 $f: |K| \to |K|$，$f_\star: H_k(|K|^k; \mathbb{Q})$ 是恒等映射，所以 $\Lambda_f = 1$。

因此 $f$ 有不动点。
另一个推论

用上面的推论，当 $|K| = D^n$ 是一个 $n$ 维的球。$f: |K| \to |K|$ 是连续映射，则 $f$ 有不动点。

因此，Lefschetz 不动点定理 $\Rightarrow$ Brouwer 不动点定理。

当 $|K|$ 是可缩的，则 $f: |K| \to |K|$ 有不动点。
例子：环面的单纯复形

如下图：

考试范围

省流：什么都考。

期中之后的重点是同调理论。

基本群和覆叠空间： + 分类定理。 + 要会算 $\pi_1$ 和 $f_\star: \pi_1(X) \to \pi_1(Y)$。

同调理论： + 具体空间计算同调群。 + Lefschetz 不动点定理，例如计算 $f_\star: H_n(X) \to H_n(X)$ 判断有没有不动点。 + Euler-Poincare 定理。

剩下的没写的不是不考，是不想记了。

完结撒花！

00. Lecture Info

1. 考核

2. 作业

3. 答疑

4. 内容

一点牢骚

01. 引入：范畴与连续映射入门

拓扑学研究的范畴

范畴的观点（Categories）

拓扑学研究的例子

连续映射

数学分析对连续映射的定义

度量 (Metric)

度量空间 (Metric Space)

基础的度量空间例子

度量空间连续性的定义

引入：球的概念

定义：开集 (Open Set)

定理 (开集)

定义：闭集 (Close Set)

关键定理 (连续性)

定义：拓扑空间 (Topological Space)

例子

定义：连续映射

*一个可能不那么典型的例子（拓扑可以非常丰富）

02. 闭集与连续映射

对闭集的研究

回忆：闭集的定义

一些例子

极限点 (limit point) 的定义

闭集一般性的定义

闭包 (closure) 的定义

稠密 (dense) 的定义

内部点 (interior point) 的定义

边界点 (frontier point / boundary point) 的定义

拓扑基 (basis / base) 的定义

对连续映射的研究

回忆：连续映射

连续映射的复合

限制到子空间的连续性

连续性的等价叙述

03. 同胚、距离与度量空间

对连续映射的进一步研究

同胚 (Homeomorphism) 的定义

连续映射的局部性质 (Local formulation of continuity)

拓扑学中的极限 (Limit)

对度量空间的研究

度量空间的扩张/延拓 (Extension Problem)

点到集合距离的定义

扩张定理 (Tietze extension theorem)

04. 度量空间的完备化

度量空间的完备化

完备的度量空间 (Complete metric space)

柯西序列 (Cauchy Sequence)

点列的极限

完备度量空间的概念

例子

度量空间的完备化 (Completion of a metric space)

度量空间间的 Isometry

度量空间完备化的唯一性 (Uniqueness of Completion)

度量空间完备化的存在性 (Existence of Completion)

05. 紧空间与Hausdorff空间

紧空间 (Compactness)

数学分析时的紧空间

闭区间的有限覆盖定理 (Heine-Borel Theorem)

紧空间 (Compact Space)

紧集 (Compact Set)

欧氏空间中的紧集（主定理）

紧集的简单性质

连续映射保持紧性

闭子集保持紧性

Hausdorff 空间

例子

Hausdorff 空间的极限存在则唯一

度量空间点列极限的叙述

Hausdorff 空间与紧集

连续双射与同胚

紧空间中无限集必有极限点

主定理的证明，必要条件

紧集与函数极值